Funções crescente, decrescente e constante
Como identificar no gráfico e na fórmula — com exemplos e exercícios resolvidos.
Este guia prático mostra como reconhecer intervalos de crescimento, decrescimento e trechos constantes. Se precisar, revise: Plano Cartesiano, Gráfico de uma Função, Zeros de Funções e Imagem de uma Função. Para muita prática, use o Banco de Questões.
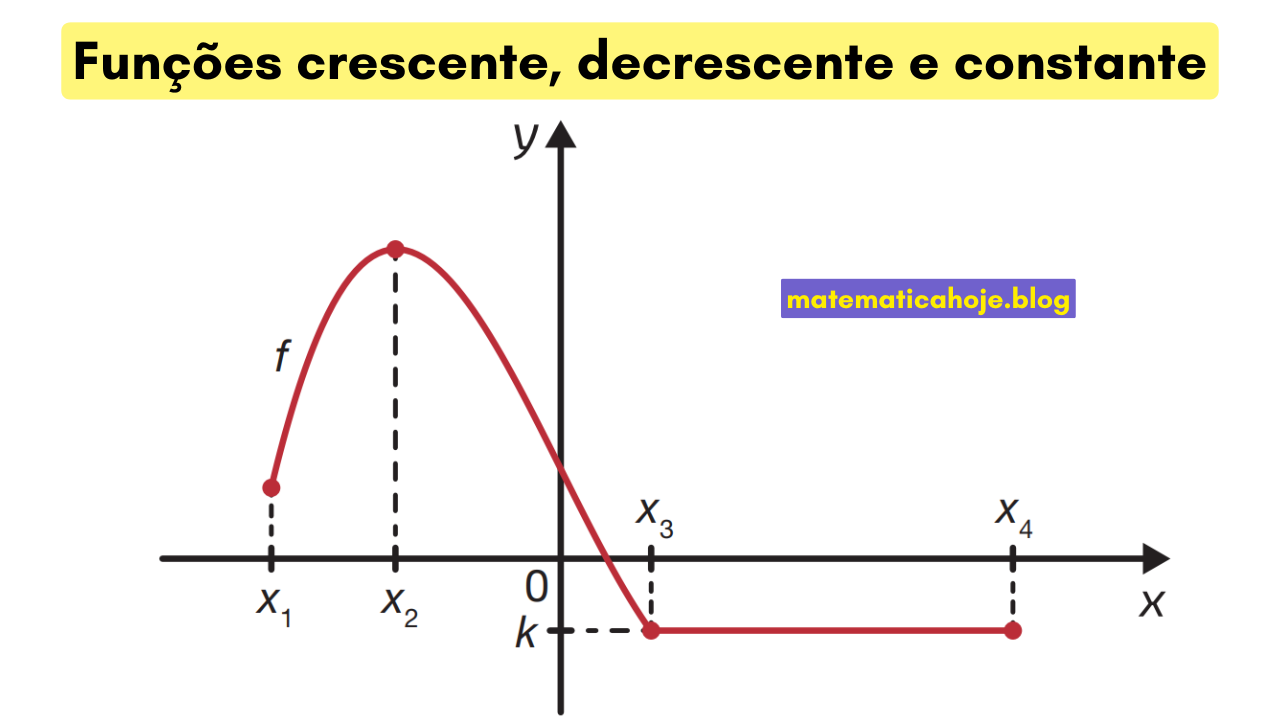
• Decrescente: se x1 < x2 ⇒ f(x1) > f(x2).
• Constante: se f(x) = k para todo x ∈ I.
(As versões “não-decrescente” / “não-crescente” usam ≤ e ≥.)
Como ler diretamente do gráfico
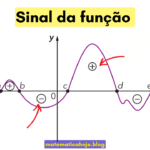
- Varra a curva da esquerda para a direita. Subindo ⇒ crescente; descendo ⇒ decrescente; reta horizontal ⇒ constante.
- No desenho: f é crescente em (x1, x2), decrescente em (x2, x3) e constante em [x3, x4], com valor k.
- Bolinha cheia inclui a extremidade; bolinha vazia exclui (define se o intervalo é aberto ou fechado).
Como decidir pela fórmula (sem Cálculo)
- Função afim f(x) = m x + b: se m > 0 é crescente; se m < 0 é decrescente; se m = 0 é constante (em toda ℝ).
- Quadrática ax² + bx + c: o vértice tem abscissa xv = −b/(2a). Se a > 0: decresce em (−∞, xv) e cresce em (xv, ∞). Se a < 0, inverte.
- Módulo |x − a|: decresce até x = a e cresce depois. Em geral, trate por partes conforme o interior do módulo muda de sinal.
- Composição/por partes: analise cada trecho e depois una os intervalos (atenção a quinas e saltos).
Com derivadas (opcional)
Se a função é diferenciável, vale o teste: f'(x) > 0 ⇒ crescente; f'(x) < 0 ⇒ decrescente; f'(x) = 0 em um intervalo ⇒ constante naquele trecho. Trocas de sinal de f'(x) costumam marcar máximos e mínimos locais.
Exemplos rápidos
| Função | Raciocínio | Intervalos |
|---|---|---|
| f(x) = 3x − 2 | Inclinação m = 3 > 0 | crescente em ℝ |
| g(x) = −2x + 5 | m = −2 < 0 | decrescente em ℝ |
| h(x) = 7 | valor fixo | constante em ℝ |
| p(x) = x² − 4x + 1 | vértice xv = 2 | decrescente em (−∞, 2); crescente em (2, ∞) |
| q(x) = |x − 3| | quebra em x = 3 | decrescente em (−∞, 3]; crescente em [3, ∞) |
Armadilhas comuns
- Confundir “não-decrescente” com “crescente”: se a função fica plana (plateau), ela não é crescente estrita.
- Trocas de comportamento costumam ocorrer em extremos (vértice da quadrática, quina do módulo, ponto onde a regra por partes muda).
- Escalas dos eixos: verifique as marcas — mudar a escala pode enganar a percepção de subida/descida.
Exercícios (múltipla escolha) com solução
1) A função f(x) = 5 − 3x é:
- crescente em ℝ
- decrescente em ℝ
- constante em ℝ
- crescente em (0, ∞) e decrescente em (−∞, 0)
Ver solução
2) Para g(x) = x² − 6x + 10, os intervalos corretos são:
- crescente em (−∞, 3); decrescente em (3, ∞)
- decrescente em (−∞, 3); crescente em (3, ∞)
- crescente em ℝ
- decrescente em ℝ
Ver solução
3) A função h(x) = |x + 1| é:
- crescente em ℝ
- decrescente em ℝ
- decrescente em (−∞, −1] e crescente em [−1, ∞)
- constante em [−1, 1]
Ver solução
4) Em p(x) = (x − 2)³, o comportamento é:
- decrescente em (−∞, 2) e crescente em (2, ∞)
- crescente em ℝ
- constante em ℝ
- crescente em (−∞, 0) e decrescente em (0, ∞)
Ver solução
5) A função por partes q(x) = { 2x + 1, se x < 0 ; −1, se 0 ≤ x ≤ 3 ; x − 4, se x > 3 } é:
- crescente em (−∞, 0), constante em [0, 3] e crescente em (3, ∞)
- decrescente em (−∞, 0), constante em [0, 3] e decrescente em (3, ∞)
- constante em ℝ
- crescente em (−∞, 0) e decrescente no resto
Ver solução
6) Se f é estritamente crescente em [a, b], então:
- f(a) = f(b)
- f é injetora em [a, b]
- f é constante em [a, b]
- não é possível afirmar
Ver solução
Continue estudando (links internos)
• Mapas Mentais de Matemática
• Roteiro ENEM Matemática
• Gráfico de uma Função
• Função do 2º Grau
• Coleção 10 eBooks de Matemática