Função do Tipo Exponencial: Entendendo os Coeficientes a, b e c

As funções exponenciais aparecem em contextos naturais e práticos, como crescimento populacional, decaimento radioativo e juros compostos. Aqui estudamos uma forma mais geral, a chamada função do tipo exponencial, dada por:

\( f(x) = b \cdot a^x + c, \quad \text{com } a>0, \; a \neq 1, \; b \neq 0 \)

Nesta função, os coeficientes a, b e c influenciam diretamente o formato do gráfico. Vamos entender cada um deles.

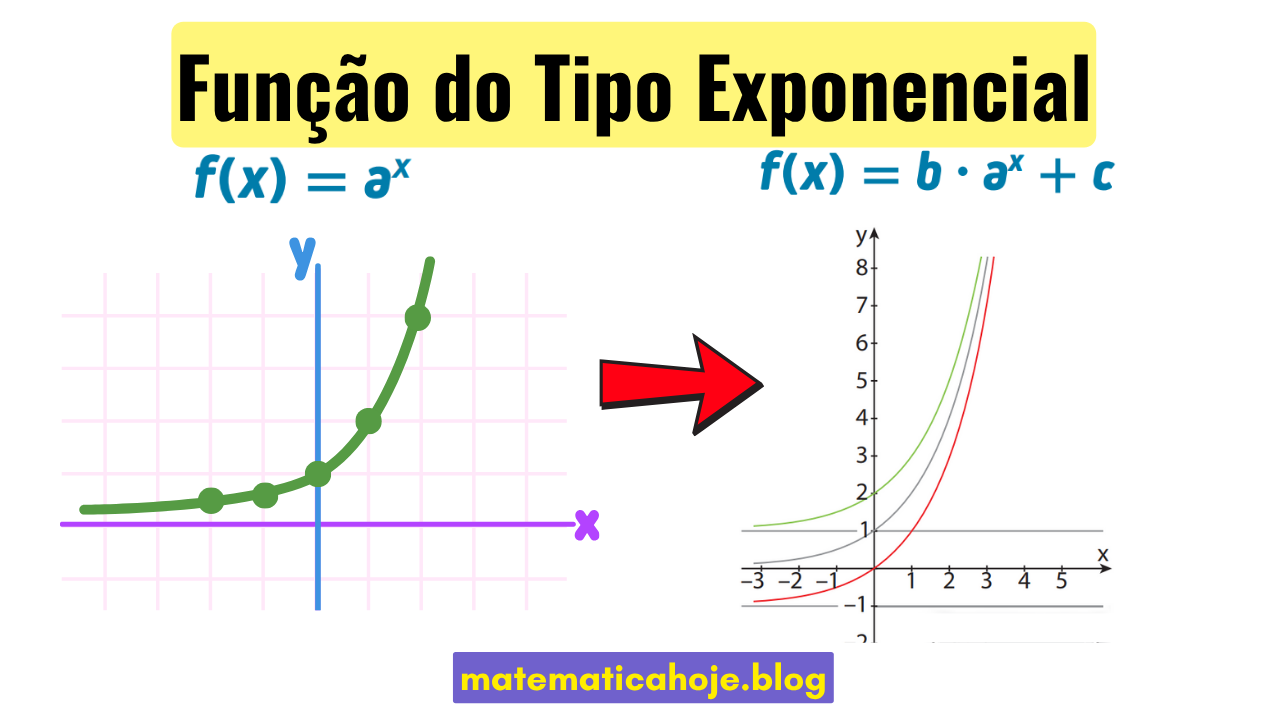
Função do tipo exponencial com coeficientes a, b e c

Influência dos coeficientes

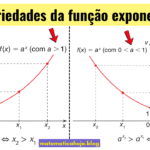
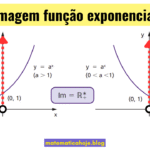
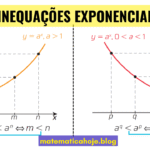
Coeficiente a: determina a base da exponenciação. Se \(a>1\), a função é crescente. Se 0 < a < 1, a função é decrescente.
Coeficiente b: atua como fator de escala vertical, influenciando a inclinação do gráfico. Se \(b<0\), ocorre uma reflexão em relação ao eixo x.
Coeficiente c: desloca o gráfico verticalmente. Valores positivos de \(c\) deslocam para cima, negativos deslocam para baixo.

Exemplos

Veja alguns exemplos de funções exponenciais e suas características:

\( f(x) = 2 \cdot 3^x \) → Crescente, base maior que 1, sem deslocamento vertical.
\( g(x) = -4 \cdot (0,5)^x + 2 \) → Decrescente, refletida no eixo x, deslocada 2 unidades para cima.
\( h(x) = (1,1)^x – 3 \) → Crescente, mas de crescimento lento, deslocada 3 unidades para baixo.

Construção de gráficos

Usando softwares de geometria dinâmica (como GeoGebra), é possível variar os valores de a, b e c e observar o efeito no gráfico. Isso facilita a compreensão da função exponencial e ajuda a construir intuições visuais.

Aplicações práticas

As funções do tipo exponencial são aplicadas em:

Ciências Naturais: crescimento populacional, dinâmica de espécies e fenômenos de radioatividade.
Economia: juros compostos e inflação.
Tecnologia: processos de decaimento digital e algoritmos matemáticos.

📥 eBook de Fórmulas Matemáticas

Tenha sempre em mãos todas as principais fórmulas, incluindo as da função exponencial.

Baixar agora

Conclusão

A função do tipo exponencial \( f(x) = b \cdot a^x + c \) amplia a função exponencial simples e permite modelar uma variedade de fenômenos. Estudar a influência dos coeficientes ajuda a compreender melhor os gráficos e suas aplicações.

Continue aprofundando seus estudos com nossos materiais: Mapas Mentais, Matemática para ENEM, 10 E-books de Matemática e o Banco de Questões.