Mapa Mental da Função Logarítmica
A função logarítmica é uma das mais importantes da Matemática, intimamente ligada à potenciação. O estudo dessa função é fundamental para compreender crescimento, escalas, fenômenos naturais e aplicações em provas como o ENEM e concursos.
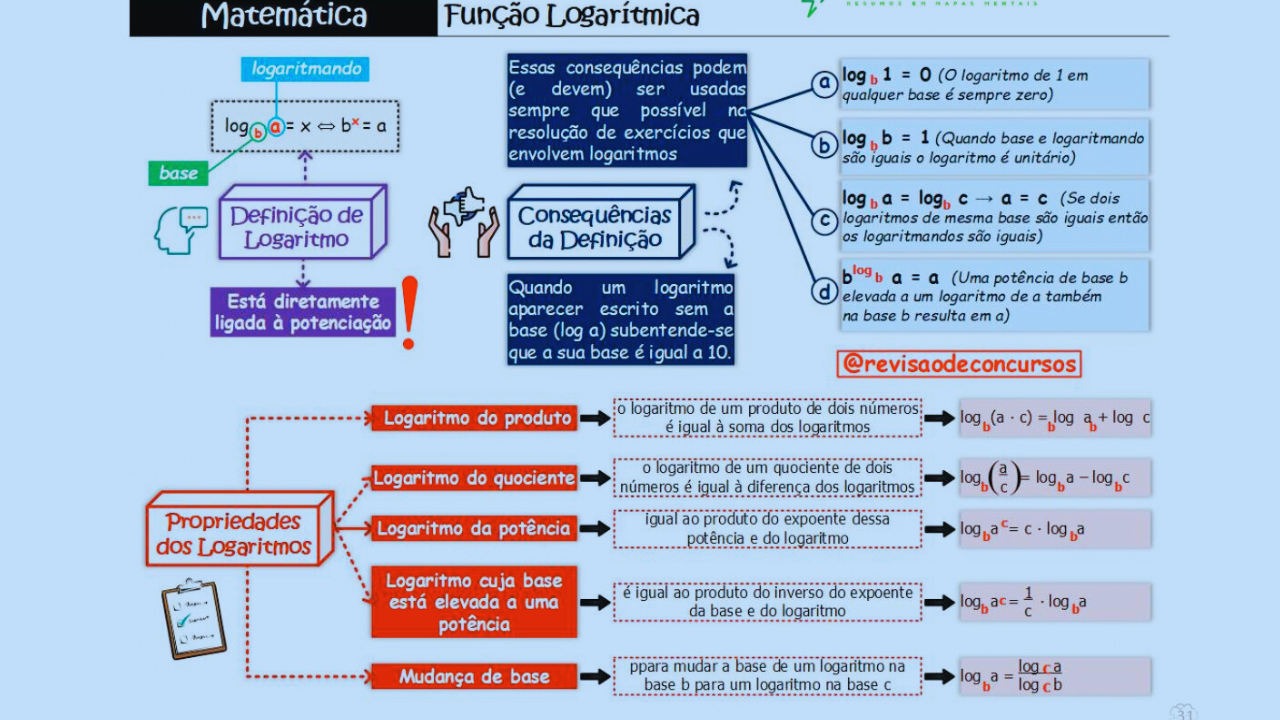
Definição
- \(b\) é a base (positiva e diferente de 1).
- \(a\) é o logaritmando (positivo).
- \(x\) é o logaritmo.
Consequências da Definição
- \(\log_{b} 1 = 0\).
- \(\log_{b} b = 1\).
- Se \(\log_{b} a = \log_{b} c\), então \(a=c\).
- \(b^{\log_{b} a} = a\).
Propriedades dos Logaritmos
- Produto: \(\log_{b}(a\cdot c)=\log_{b}a + \log_{b}c\).
- Quociente: \(\log_{b}\left(\frac{a}{c}\right)=\log_{b}a – \log_{b}c\).
- Potência: \(\log_{b}(a^k)=k\cdot\log_{b}a\).
- Base elevada a potência: \(\log_{b^k} a=\frac{1}{k}\log_{b} a\).
- Mudança de base: \(\log_{b}a = \frac{\log_{c}a}{\log_{c}b}\).
Exemplo prático
Vamos calcular \(\log_{2} 32\). Como \(32=2^5\), segue que \(\log_{2} 32 = 5\).
Exercício proposto
Simplifique: \(\log_{3} 27 + \log_{3} 9\).
Solução
Aplicando a propriedade do produto:
\(\log_{3}(27\cdot 9) = \log_{3}(243)\).
Como \(243=3^5\), temos \(\log_{3} 243 = 5\).
📥 Estude com material completo
Para revisar todas as propriedades de logaritmos, baixe o eBook de Fórmulas Matemáticas.
Baixar agoraConclusão
A função logarítmica e suas propriedades são essenciais para a resolução de problemas que envolvem crescimento e decaimento, equações exponenciais e até mesmo escalas como dB (decibéis) e pH. Praticar exercícios com as propriedades é a melhor forma de dominar o tema.













