A análise combinatória é um ramo da matemática que ajuda a resolver problemas envolvendo contagem e organização de elementos. De forma simples, ela responde a perguntas como: “De quantas maneiras diferentes podemos organizar, escolher ou agrupar coisas?”
O que é análise combinatória?
A análise combinatória é o estudo das diferentes formas de combinar ou organizar elementos em um conjunto. Ela fornece ferramentas para calcular essas possibilidades de maneira eficiente, sem a necessidade de listar manualmente todas as opções. Por exemplo, em vez de contar uma por uma as maneiras de organizar 5 pessoas em uma fila, usamos as fórmulas da análise combinatória para obter a resposta de forma rápida.
Por que a análise combinatória é importante?
A análise combinatória está presente em muitas situações do dia a dia e é especialmente útil para resolver questões em concursos e vestibulares. Além disso, ela tem aplicações práticas em áreas como estatística, probabilidade, ciência de dados, informática e até mesmo na organização de eventos.
- No dia a dia: Imagine que você tem 3 camisetas e 2 calças. Com quantas combinações diferentes você pode montar um look? A análise combinatória responde!
- Em concursos: Questões como “De quantas maneiras diferentes um comitê de 3 pessoas pode ser formado a partir de um grupo de 10?” são muito comuns em provas.
- Em tecnologia: Ela é usada em criptografia e em algoritmos que organizam grandes volumes de dados.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
Exemplos práticos para entender melhor
- Códigos de segurança: Considere um cadeado que precisa de um código de 3 dígitos para ser aberto. Se cada dígito pode variar de 0 a 9, quantas combinações diferentes existem? A análise combinatória nos ajuda a calcular rapidamente: são 10 x 10 x 10 = 1.000 combinações possíveis.
- Jogos e apostas: Em uma loteria onde você escolhe 6 números entre 60 disponíveis, quantas combinações diferentes podem ser feitas? Essa é uma aplicação direta das fórmulas de combinação.
Com esses exemplos, fica claro que a análise combinatória não é apenas uma ferramenta teórica, mas algo que usamos constantemente, muitas vezes sem perceber. E mais: dominar esse tema pode ser um diferencial importante para alcançar sucesso em provas e na vida prática!
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Conceitos Fundamentais da Análise Combinatória
A análise combinatória é construída sobre alguns conceitos básicos que formam a base para resolver problemas de contagem, organização e escolha. Esses conceitos são ferramentas que nos ajudam a compreender como organizar elementos em diferentes contextos, desde situações simples, como combinar roupas, até questões mais complexas, como calcular probabilidades.
Entre os principais pilares da análise combinatória estão o fatorial, princípio fundamental da contagem, as permutações, os arranjos e as combinações. Cada um desses conceitos possui aplicações específicas, mas todos compartilham o objetivo de facilitar a contagem de possibilidades de maneira rápida e eficiente.
Neste capítulo, exploraremos esses fundamentos de forma clara e prática, utilizando exemplos do dia a dia para simplificar o entendimento e mostrar como eles estão presentes em diversas situações do cotidiano.
Fatorial: O Alicerce da Análise Combinatória
O fatorial é um dos conceitos mais básicos e essenciais da análise combinatória. Representado pelo símbolo “!”, ele aparece em diversos cálculos e fórmulas relacionados à organização, arranjos e combinações de elementos. Entender o fatorial é o primeiro passo para dominar problemas de contagem de maneira eficiente.
O Que é Fatorial?
O fatorial de um número natural nn, representado por n!, é o resultado da multiplicação de todos os números inteiros positivos de 1 até nn. Em outras palavras:
n! = n×(n − 1)×(n − 2)×⋯×1
Exemplos Práticos:
- 3! = 3×2×1 = 6
- 5! = 5×4×3×2×1 = 120
- 1! = 1 (por definição)
- 0! = 1 (um caso especial, definido por convenção)
O fatorial cresce rapidamente à medida que o valor de nn aumenta. Por exemplo:
- 6! = 720
- 10! = 3.628.800
Por Que o Fatorial É Importante?
O fatorial é essencial na análise combinatória porque é usado para calcular permutações, arranjos e combinações. Ele ajuda a determinar o número de maneiras de organizar ou escolher elementos de um conjunto.
Exemplo do Dia a Dia:
Imagine que você tem 5 livros diferentes e quer organizá-los em uma estante. Quantas maneiras diferentes você pode fazer isso?
A resposta é dada por 5!, que calcula todas as ordens possíveis. Nesse caso:
5! = 5×4×3×2×1 = 120
Portanto, há 120 maneiras de organizar esses livros.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
Fatorial e Situações Reais
1. Planejamento de Atividades
Suponha que você tenha 4 tarefas para realizar durante o dia. A ordem das tarefas importa, pois afeta o andamento do seu dia. Quantas sequências diferentes você pode criar?
A resposta é 4!:
4! = 4×3×2×1 = 24 sequências possíveis
2. Jogos de Tabuleiro
Em um jogo onde 3 jogadores devem escolher uma ordem para jogar, o número de possibilidades é 3!:
3! = 3×2×1 = 6
Assim, há 6 ordens possíveis para organizar os jogadores.
3. Senhas e Códigos
Se um cadeado exige uma senha de 4 dígitos distintos e a ordem dos dígitos importa, o número de combinações possíveis é dado por 4!, ou 24 combinações.
Exemplos:
1 – Calcular 10!/9!
Solução:
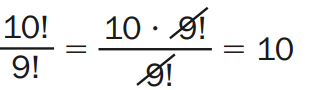
2 – Calcular 10!/8!
Solução:
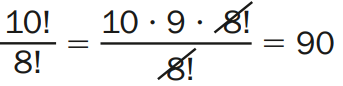
3 – Calcular 12!/(9! 3!)
Solução:
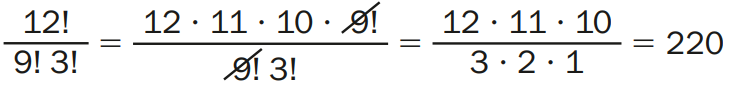
4 – Simplifique a expressão 20!/18!
Solução:
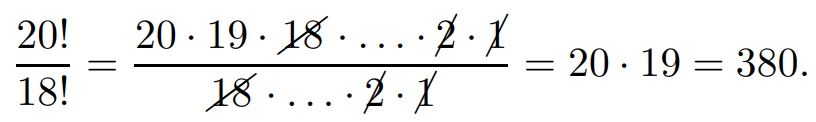
5 – Simplifique a expressão 1/5! − 1/6!
Solução: veja que o mínimo múltiplo comum entre 6! e 5! ´e igual a 6!; ademais, temos que
6!/5! = 6
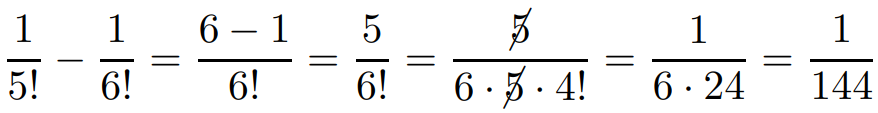
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Princípio Fundamental da Contagem
O Princípio Fundamental da Contagem (PFC) é uma regra simples e poderosa que permite calcular o número total de possibilidades em situações que envolvem escolhas ou etapas consecutivas. Ele funciona multiplicando o número de opções disponíveis em cada etapa.
O Que É o PFC?
Se você tem duas ou mais escolhas independentes, o total de combinações possíveis é obtido multiplicando o número de opções de cada escolha. Isso facilita problemas que, de outra forma, poderiam exigir longas listagens.
Exemplos Práticos
1. Escolhendo uma Roupa
Você tem:
- 2 pares de sapatos (preto e branco);
- 3 calças (jeans, social e esportiva);
- 2 blusas (camiseta e camisa).
Quantos looks diferentes podem ser formados?
Solução:
2 (sapatos)×3 (calças)×2 (blusas) = 12 looks
2. Planejando um Jantar
Um jantar possui:
- 3 entradas (sopa, salada, brusqueta);
- 2 pratos principais (carne ou peixe).
Quantos pratos completos podem ser servidos?
Solução:
3 (entradas)×2 (pratos principais) = 6 combinações
3. Criando uma Senha
Uma senha tem 4 dígitos, e cada dígito pode variar de 0 a 9. Quantas senhas podem ser criadas?
Solução:
10×10×10×10 = 10.000 senhas
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Por Que o PFC É Útil?
O PFC é a base para resolver problemas de contagem de forma eficiente. Ele é essencial para entender conceitos como permutações e combinações e aparece em situações práticas, como planejamento, organização e até criação de senhas.
Exercícios resolvidos
1) (Enem) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada. O diretor sabe que algum aluno acertará a resposta porque há:
a) 10 alunos a mais do que possíveis respostas distintas.
b) 20 alunos a mais do que possíveis respostas distintas.
c) 119 alunos a mais do que possíveis respostas distintas.
d) 260 alunos a mais do que possíveis respostas distintas.
e) 270 alunos a mais do que possíveis respostas distintas.
Solução
O número de possíveis respostas será igual ao produto das quantidades de personagens, objetos e cômodos.
5 · 6 · 9 = 270.
Como o número de alunos é 280, então a diferença entre a quantidade de número de alunos e a quantidade de possibilidades (270) é 10. (280 – 270 = 10)
Resposta: alternativa A.
Diferença entre Permutação, Combinação e Arranjo
A análise combinatória se baseia em três conceitos principais: permutação, combinação e arranjo. Embora esses termos sejam frequentemente confundidos, cada um tem uma aplicação específica dependendo do problema que estamos resolvendo. A diferença entre eles está, principalmente, na importância da ordem e no número de elementos considerados.
1. Permutação
A permutação trata da organização de todos os elementos de um conjunto, levando em conta a ordem. É usada quando todos os itens disponíveis serão organizados em diferentes sequências.
Exemplo:
Quantas formas diferentes você pode organizar 3 livros em uma prateleira?
- Livros: A, B e C
- Possibilidades: ABC, ACB, BAC, BCA, CAB, CBA (6 ao todo).
A ordem é fundamental aqui, pois ABC é diferente de BAC.
2. Arranjo
O arranjo considera apenas uma parte dos elementos do conjunto, mas a ordem também importa. É usado quando você precisa organizar um subconjunto de itens.
Exemplo:
De 5 amigos, quantos grupos de 2 pessoas podem ser formados para ocupar os papéis de líder e vice-líder?
- Grupo 1: Ana e João (ordem importa, pois Ana é líder e João vice).
- Grupo 2: João e Ana (ordem inversa é uma nova combinação).
Nesse caso, a ordem define diferentes arranjos.
3. Combinação
Na combinação, a ordem não importa e estamos interessados apenas no grupo formado, independentemente da disposição dos itens.
Exemplo:
De 5 frutas, quantas duplas podem ser escolhidas?
- Grupo 1: Maçã e Banana.
- Grupo 2: Banana e Maçã (são o mesmo grupo, pois a ordem não importa).
Aqui, consideramos apenas o conjunto formado, sem se preocupar com a disposição.
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Resumo das Diferenças
| Conceito | Importância da Ordem | Número de Elementos Considerados |
|---|---|---|
| Permutação | Sim | Todos os elementos do conjunto |
| Arranjo | Sim | Apenas parte dos elementos |
| Combinação | Não | Apenas parte dos elementos |
Esses conceitos são fundamentais para resolver problemas de contagem e organização. Compreendê-los ajuda a escolher a abordagem correta para cada tipo de questão.
Permutações
As permutações são uma das bases da análise combinatória e envolvem a organização de elementos de um conjunto em diferentes ordens. Aqui, a ordem dos elementos é essencial, e existem dois tipos principais de permutação: simples e com elementos repetidos.
1. Permutação Simples
A permutação simples é utilizada quando todos os elementos de um conjunto são distintos, e queremos organizá-los de todas as maneiras possíveis.
Fórmula:
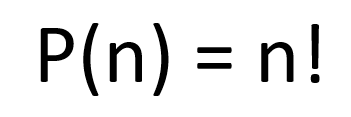
Aqui, n!n! representa o fatorial de n, ou seja, o produto de todos os números inteiros de n até 1.
Exemplo Prático:
Imagine que você tem 3 objetos diferentes: A, B e C. Quantas maneiras diferentes você pode organizá-los?
- Possibilidades: ABC, ACB, BAC, BCA, CAB, CBA.
- Total:
P(3) = 3! = 3×2×1 = 6
Portanto, existem 6 permutações possíveis para esses 3 objetos.
2. Permutação com Elementos Repetidos
A permutação com elementos repetidos ocorre quando o conjunto tem elementos que se repetem. Nesse caso, o número total de permutações é reduzido, pois trocar a posição de elementos iguais não gera uma nova organização.
Fórmula:
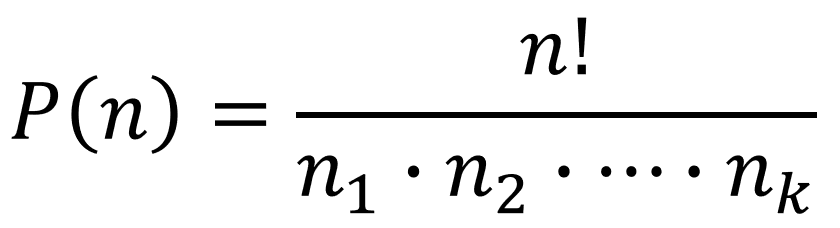
- n: número total de elementos.
- n1, n2, …,nk: quantidades de elementos repetidos.
Exemplo Prático:
Quantas palavras diferentes podem ser formadas com as letras da palavra “ANA”?
- Total de letras: 3 (A, N, A).
- A letra “A” se repete 2 vezes.
Cálculo:
P = 3!/2! = 6/2 = 3
Palavras possíveis: ANA, AAN, NAA.
Resumo das Diferenças
| Tipo de Permutação | Elementos Iguais? | Fórmula | Exemplo Simples |
|---|---|---|---|
| Simples | Não | P(n) = n! | Organizar 3 livros distintos |
| Com Elementos Repetidos | Sim | 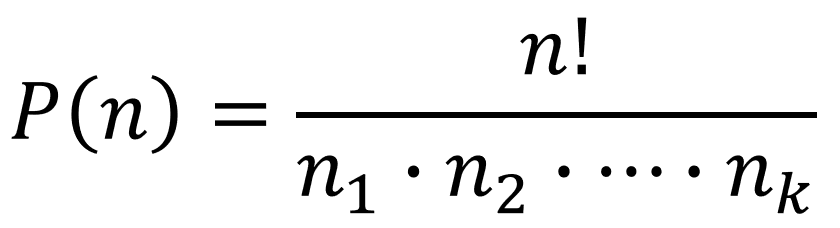 | Formar palavras com “ANA” |
As permutações são amplamente aplicáveis em problemas que envolvem organização e ordem, como arranjos de objetos, planejamento de tarefas ou formação de senhas. Entender a diferença entre os tipos de permutação ajuda a escolher a abordagem correta para cada problema!
“Quer dominar os cálculos de possibilidades e resolver problemas de contagem com facilidade? Confira nosso artigo completo sobre as Fórmulas da Análise Combinatória e aprenda como aplicá-las no seu dia a dia com exemplos claros e objetivos!
Arranjos
Os arranjos são um conceito fundamental da análise combinatória que lidam com a organização de uma parte dos elementos de um conjunto, considerando que a ordem importa. Existem dois tipos principais de arranjos: simples e com repetição, cada um aplicável em situações específicas.
Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
1. Arranjo Simples
O arranjo simples ocorre quando escolhemos kk elementos de um conjunto com nn elementos totais, sem permitir repetições, e organizamos esses elementos em diferentes ordens.
Fórmula:
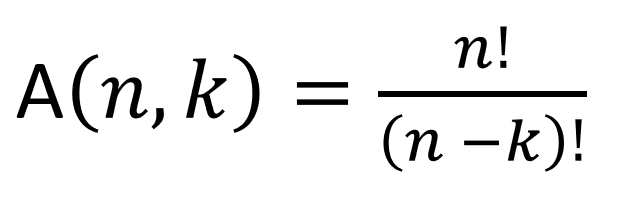
- n: número total de elementos no conjunto.
- k: número de elementos escolhidos.
Exemplo Prático:
Imagine que você tem 6 candidatos para 3 cargos diferentes (presidente, vice-presidente e tesoureiro). Quantas formas diferentes é possível organizar essas posições?
Solução:
- Total de candidatos (n): 6.
- Cargos a serem preenchidos (k): 3.
Cálculo:
A(6,3) = 6!/(6−3)! = (6×5×4×3!)/3! = 6×5×4 = 120
Portanto, existem 120 formas diferentes de organizar os 3 cargos.
2. Arranjo com Repetição
O arranjo com repetição ocorre quando os elementos escolhidos podem ser repetidos. Nesse caso, cada elemento do conjunto pode ser usado várias vezes em diferentes combinações.
Fórmula:
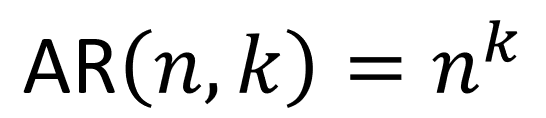
- n: número total de elementos no conjunto.
- k: número de elementos escolhidos, permitindo repetições.
Exemplo Prático:
Imagine que você está criando uma senha de 3 caracteres usando as letras A, B e C, e as letras podem ser repetidas. Quantas senhas diferentes podem ser criadas?
Solução:
- Total de letras (n): 3.
- Número de caracteres da senha (k): 3.
Cálculo:
AR(3,3) = 33 = 27
Portanto, é possível formar 27 senhas diferentes com repetição.
Diferenças Entre Arranjo Simples e Arranjo com Repetição
| Tipo de Arranjo | Repetição Permitida? | Fórmula | Exemplo Prático |
|---|---|---|---|
| Arranjo Simples | Não | 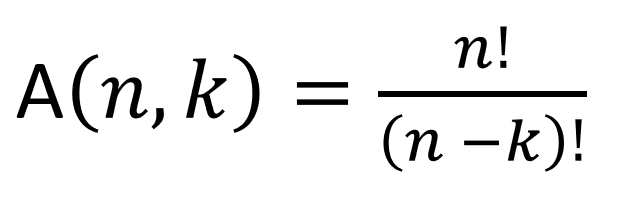 | Organizar candidatos em cargos distintos. |
| Arranjo com Repetição | Sim | 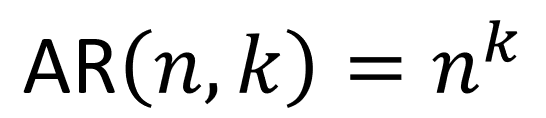 | Criar senhas onde caracteres se repetem. |
Conclusão
Os arranjos são ferramentas essenciais para resolver problemas que envolvem seleção e organização de elementos, levando em conta a ordem e, às vezes, a repetição. Saber quando usar cada tipo de arranjo é fundamental para resolver questões de forma eficiente e precisa. Seja para organizar cargos ou criar combinações repetitivas, os arranjos são indispensáveis na análise combinatória!
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Combinação
A combinação é um dos conceitos centrais da análise combinatória, utilizado para calcular o número de maneiras de selecionar elementos de um conjunto quando a ordem não importa. Dependendo do problema, ela pode ser classificada como simples ou composta. Ambas têm aplicações práticas em várias situações do dia a dia, como formação de grupos, escolha de itens ou seleções em jogos.
1. Combinação Simples
A combinação simples é usada quando selecionamos kk elementos de um conjunto com nn elementos, sem levar em conta a ordem e sem permitir repetições.
Fórmula da Combinação Simples:

- n: número total de elementos no conjunto.
- k: número de elementos escolhidos.
- !: fatorial (produto de todos os números inteiros positivos até o número dado).
Exemplo Prático:
Formação de Grupos:
Uma escola tem 6 alunos e precisa formar um grupo de 3 para representar a turma em um evento. Quantos grupos diferentes podem ser formados?
Solução:
- Total de alunos (n): 6.
- Número de escolhidos (k): 3.
Cálculo:
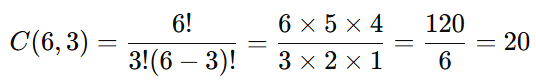
Portanto, é possível formar 20 grupos diferentes.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
2. Combinação Composta
A combinação composta, também chamada de combinação com repetição, ocorre quando os elementos selecionados podem ser repetidos. Essa técnica é usada em situações onde o número de escolhas (k) é maior ou igual ao número de elementos disponíveis (n).
Fórmula da Combinação Composta:

- n: número de elementos distintos no conjunto.
- p: número de elementos a serem escolhidos (com repetição).
- !: fatorial.
Exemplo Prático:
Escolha de Sabores:
Uma sorveteria tem 3 sabores de sorvete (baunilha, chocolate e morango) e você deseja escolher 4 bolas, podendo repetir sabores. Quantas combinações diferentes podem ser feitas?
Solução:
- Total de sabores (n): 3.
- Quantidade de bolas (p): 4.
Cálculo:
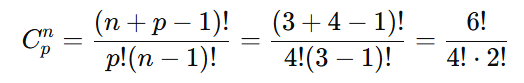
Expandindo os fatoriais:
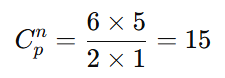
Portanto, existem 15 combinações diferentes de sorvetes.
“Quer dominar os cálculos de possibilidades e resolver problemas de contagem com facilidade? Confira nosso artigo completo sobre as Fórmulas da Análise Combinatória e aprenda como aplicá-las no seu dia a dia com exemplos claros e objetivos!
Diferenças Entre Combinação Simples e Composta
| Característica | Combinação Simples | Combinação Composta |
|---|---|---|
| Repetição de Elementos | Não é permitida | É permitida |
| Fórmula |  |  |
| Exemplo Prático | Formar grupos de alunos distintos. | Escolher sabores de sorvete com repetição. |
Aplicações Práticas
- Combinação Simples:
- Formação de grupos ou comissões.
- Escolha de números para jogos de loteria.
- Seleção de itens em um cardápio sem repetições.
- Combinação Composta:
- Escolha de itens repetíveis, como sabores de sorvete ou combinações de ingredientes.
- Distribuição de recursos em projetos.
- Problemas de seleção com repetição em pesquisa científica.
Conclusão
Tanto a combinação simples quanto a combinação composta são ferramentas essenciais para resolver problemas de seleção sem se preocupar com a ordem dos elementos. Saber diferenciar as duas abordagens é crucial para aplicar a análise combinatória de forma eficiente. Enquanto a combinação simples é usada quando não há repetição, a combinação composta permite selecionar elementos que podem se repetir, tornando-a ideal para situações mais flexíveis e variadas.
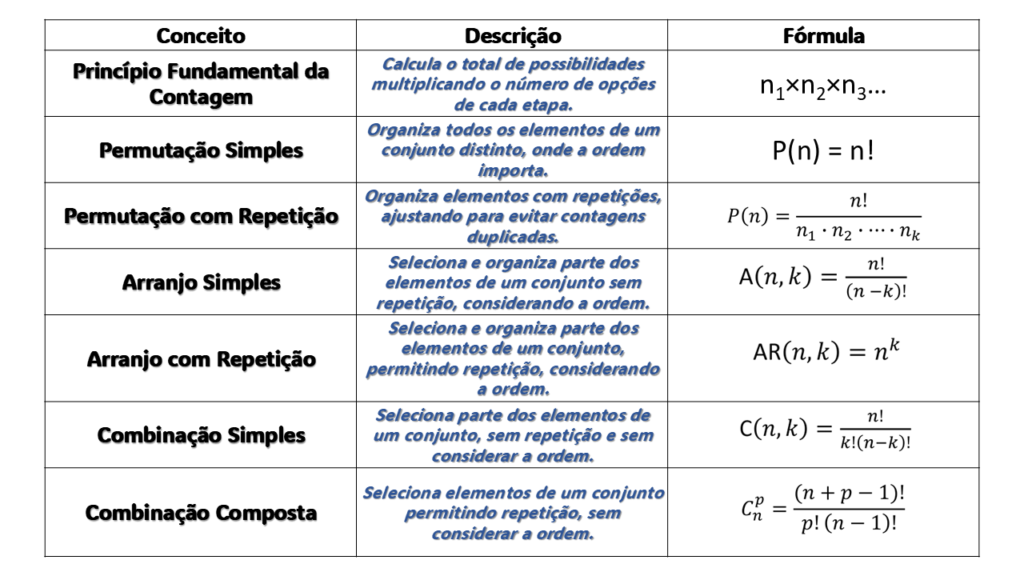
Tabela de Resumo: Fórmulas da Análise Combinatória
| Conceito | Descrição | Fórmula |
|---|---|---|
| Princípio Fundamental da Contagem | Multiplica o número de possibilidades de cada etapa independente. | n1×n2×n3× … |
| Permutação Simples | Número de maneiras de organizar todos os elementos de um conjunto onde todos são diferentes. | P(n) = n! |
| Permutação com Repetição | Número de maneiras de organizar elementos de um conjunto com itens repetidos. | 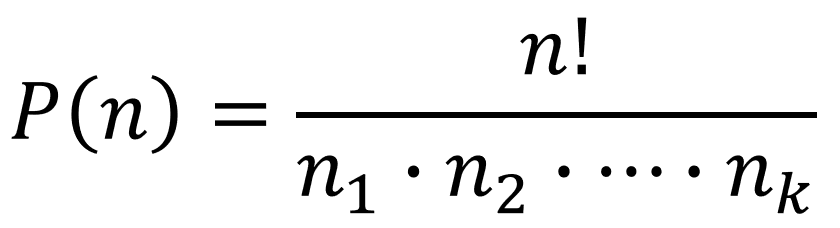 |
| Arranjo Simples | Organização de parte dos elementos de um conjunto, sem repetição, considerando a ordem. | 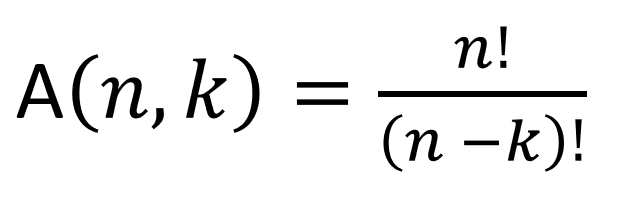 |
| Arranjo com Repetição | Organização de parte dos elementos de um conjunto, permitindo repetição, considerando a ordem. | 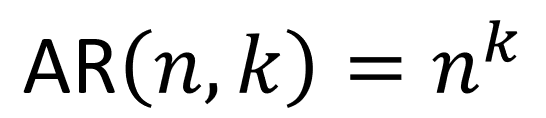 |
| Combinação Simples | Seleção de parte dos elementos de um conjunto, sem repetição, onde a ordem não importa. |  |
| Combinação Composta | Seleção de elementos de um conjunto, permitindo repetição, onde a ordem não importa. |  |
Essa tabela resume todas as fórmulas fundamentais da análise combinatória, permitindo uma visão clara e rápida para resolver problemas de contagem, organização e seleção.
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Casos Especiais na Análise Combinatória
A análise combinatória é uma ferramenta poderosa para resolver problemas de contagem, mas nem sempre os casos se enquadram nos conceitos mais simples de permutação, arranjo e combinação. Alguns problemas envolvem distribuição de objetos, restrições específicas ou até condições que tornam a solução mais complexa.
Neste artigo, exploraremos esses casos especiais e apresentaremos exemplos práticos e resolvidos para facilitar o entendimento.
1. Distribuição de Objetos em Caixas
A distribuição de objetos em caixas é um problema clássico na análise combinatória, e sua solução depende de condições específicas, como o número de caixas, a possibilidade de repetição e se as caixas estão rotuladas.
Casos Comuns:
Objetos distintos, caixas distintas:
Cada objeto pode ser colocado em qualquer caixa. O número total de distribuições é dado por:
nk
Onde n é o número de caixas e k é o número de objetos.
Exemplo:
Quantas maneiras existem para distribuir 3 livros diferentes em 2 caixas distintas?
n=2, k=3 ⟹ 23 =8 distribuições
Objetos idênticos, caixas distintas:
Usamos a fórmula da combinação composta para calcular o número de distribuições:
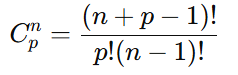
Onde n é o número de caixas e pp é o número de objetos.
Exemplo:
Distribuir 4 doces idênticos em 3 caixas distintas.
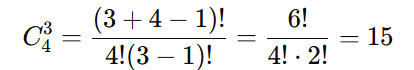
Objetos distintos, caixas idênticas:
Aqui, o problema envolve condições mais específicas e muitas vezes requer enumeração manual ou uso de fórmulas avançadas.
2. Análise Combinatória com Restrições
Quando o problema impõe restrições, precisamos adaptar os cálculos de forma estratégica. Alguns exemplos incluem:
1. Restrições de Ordem
Exemplo: Em quantas maneiras 5 pessoas podem se sentar em uma fila, se Ana e João devem ficar juntos?
Solução:
- Considere Ana e João como uma única “unidade” para preservar a restrição.
- Agora temos 4 “unidades” para organizar: (Ana e João), Pessoa 1, Pessoa 2, Pessoa 3.
- As 4 unidades podem ser organizadas de: 4!=24 maneiras
- Dentro da “unidade”, Ana e João podem trocar de posição: 2! = 2 maneiras
- Total: 24×2 = 48 maneiras
2. Restrições de Exclusão
Exemplo: Quantos números de 3 dígitos podem ser formados usando os dígitos 1, 2, 3, 4 e 5, sem repetir dígitos, e começando com um número ímpar?
Solução:
- O primeiro dígito deve ser ímpar: 1, 3, 5 (3 opções).
- O segundo dígito pode ser qualquer um dos restantes (4 opções).
- O terceiro dígito será um dos que sobrarem (3 opções).
Total: 3×4×3 = 36 números
3. Exemplos Resolvidos de Problemas Avançados
Exemplo 1: Formando Palavras com Restrições
Quantas palavras podem ser formadas com as letras da palavra “BANANA”, de modo que as vogais fiquem juntas?
Solução:
- Considere as vogais A, A, A como uma única “unidade”.
- O conjunto a ser organizado é: (AAA), B, N, N (4 unidades).
- Total de permutações: P = 4!/2! = 24/2 = 12
- Dentro da “unidade” (AAA), as vogais são idênticas, então não há reorganização.
- Total: 12 palavras
Exemplo 2: Distribuindo Presentes
De quantas maneiras 4 presentes distintos podem ser distribuídos entre 3 crianças, de forma que cada criança receba pelo menos um presente?
Solução:
Distribua 1 presente para cada criança (3 crianças recebem 1 presente cada).
Escolha 3 presentes dos 4 disponíveis:
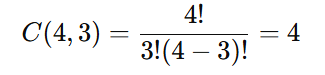
O presente restante pode ser dado a qualquer uma das 3 crianças: 3 opções
Total: 4×3 = 12 maneiras
Resumo das Estratégias para Casos Especiais
| Situação | Estratégia |
|---|---|
| Distribuição de objetos | Identificar se os objetos e caixas são distintos ou idênticos. |
| Restrições de agrupamento | Tratar os itens agrupados como uma única unidade. |
| Restrições de exclusão | Excluir opções proibidas antes de calcular as combinações ou permutações. |
| Problemas complexos com repetição ou exclusão | Usar métodos combinatórios compostos ou técnicas de contagem manual. |
Conclusão
Os casos especiais da análise combinatória exigem adaptação às condições específicas de cada problema. Seja distribuindo objetos, lidando com restrições ou resolvendo problemas mais avançados, a chave é entender as características do problema e aplicar as estratégias adequadas. Com prática, essas técnicas tornam-se ferramentas poderosas para enfrentar desafios combinatórios!
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!













