A matemática financeira exercícios é uma ferramenta essencial para resolver problemas relacionados a finanças, investimentos, empréstimos, e planejamento econômico. Aqui, apresentamos um artigo focado em exercícios resolvidos, abordando os principais conceitos da área.
Exercício 1: Juros Simples
Uma pessoa investiu R$ 5.000,00 a uma taxa de juros simples de 1,5% ao mês. Após 8 meses, qual será o montante final?
Solução:
A fórmula para o montante no regime de juros simples é:
M = C + J
O valor dos juros é calculado por:
J = C ⋅ i ⋅ t
Onde:
- ( C = 5.000 ) (capital inicial),
- ( i = 0,015 ) (taxa de juros em decimal),
- ( t = 8 ) (tempo em meses).
Substituindo na fórmula dos juros:
J = 5.000 ⋅ 0,015 ⋅ 8 = 600
Agora, calculamos o montante:
M = 5.000 + 600 = 5.600
Resposta: O montante final será R$ 5.600,00.
Exercício 2: Juros Compostos
Um valor de R$ 10.000,00 foi investido a uma taxa de 2% ao mês, em juros compostos. Qual será o montante acumulado após 6 meses?
Solução:
A fórmula para o montante em juros compostos é:
M = C ⋅ (1 + i)t
Substituindo os valores:
- ( C = 10.000 ),
- ( i = 0,02 ),
- ( t = 6 ):
M = 10.000 ⋅ (1 + 0,02)6
M = 10.000 ⋅(1,02)6 ≈ 10.000 ⋅ 1,12649 ≈ 11.264,90
Resposta: O montante será aproximadamente R$ 11.264,90.
Exercício 3: Cálculo de Taxa Efetiva
Um banco oferece uma taxa nominal de 12% ao ano, com capitalização mensal. Qual é a taxa efetiva anual?
Solução:
A fórmula da taxa efetiva é:
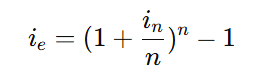
Onde:
- ( in = 0,12 ) (taxa nominal anual),
- ( n = 12 ) (número de períodos no ano).
Substituindo:
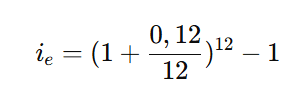
ie = (1 + 0,01)12 – 1 ≈ 1,126825 – 1 ≈ 0,126825
Convertendo para porcentagem:
ie ≈ 12,6825\%
Resposta: A taxa efetiva anual é aproximadamente 12,68%.
Exercício 4: Valor Presente
Quanto devo investir hoje para obter R$ 15.000,00 em 3 anos, sabendo que a taxa de juros compostos é de 1,5% ao mês?
Solução:
A fórmula do valor presente é:
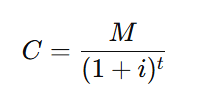
Substituindo os valores:
- ( M = 15.000 ),
- ( i = 0,015 ),
- ( t = 36 ) (meses):

Resposta: Deve-se investir aproximadamente R$ 9.108,80.
Exercício 5: Sistema de Amortização Constante (SAC)
Um empréstimo de R$ 12.000,00 será quitado em 4 parcelas mensais pelo sistema SAC, com taxa de juros de 1% ao mês. Qual o valor das parcelas?
Solução:
No sistema SAC:
- O valor da amortização é constante e dado por ( A = C/n ),
- Os juros são calculados sobre o saldo devedor.
Amortização:
A = 12.000/4 = 3.000
Parcelas:
- 1ª parcela: ( 3.000 + (12.000 ⋅ 0,01) = 3.000 + 120 = 3.120 ),
- 2ª parcela: ( 3.000 + (9.000 ⋅ 0,01) = 3.000 + 90 = 3.090 ),
- 3ª parcela: ( 3.000 + (6.000 ⋅ 0,01) = 3.000 + 60 = 3.060 ),
- 4ª parcela: ( 3.000 + (3.000 ⋅ 0,01) = 3.000 + 30 = 3.030 ).
Resposta: As parcelas são ( 3.120, 3.090, 3.060, ) e ( 3.030 ).
Esses exemplos de matemática financeira exercícios mostram como aplicar fórmulas de Matemática Financeira a problemas práticos. Para aprofundar o estudo, explore temas como taxas equivalentes, sistemas de amortização e cálculo de rendas perpétuas.
Gostou do conteúdo? Deixe seu comentário ou compartilhe com quem está estudando para concursos ou aprendendo sobre finanças!













