Na trigonometria, a Lei dos Senos e a Lei dos Cossenos são fundamentais para resolver triângulos, especialmente quando não estamos lidando com triângulos retângulos. Estas leis nos permitem calcular lados e ângulos desconhecidos em triângulos quaisquer, utilizando apenas algumas medidas conhecidas. Neste artigo, exploraremos em detalhes essas duas leis, suas aplicações e exemplos práticos.

Lei dos Senos

A Lei dos Senos relaciona os comprimentos dos lados de um triângulo com os senos dos ângulos opostos a esses lados. Ela é especialmente útil em triângulos que não são retângulos, onde o Teorema de Pitágoras não pode ser aplicado diretamente.

Enunciado da Lei dos Senos:

Em qualquer triângulo, a razão entre o comprimento de um lado e o seno do ângulo oposto a esse lado é constante para todos os três lados do triângulo.

Matematicamente, isso é expresso como:

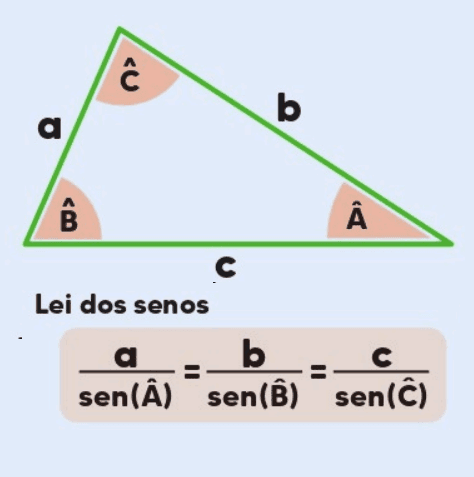
onde:

• a, b, c são os comprimentos dos lados do triângulo,
• A, B, C são os ângulos opostos a esses lados.

Aplicações da Lei dos Senos

A Lei dos Senos é particularmente útil em dois casos:

1. Quando conhecemos dois ângulos e um lado: Podemos usar a Lei dos Senos para encontrar os outros dois lados.
2. Quando conhecemos dois lados e o ângulo oposto a um desses lados: Podemos usar a Lei dos Senos para encontrar o ângulo oposto ao outro lado.

Exemplo de Aplicação

Problema: Em um triângulo, temos A=30°, B=45° e c=10. Calcule o lado a

Resolução: Primeiro, calculamos o terceiro ângulo usando a soma dos ângulos internos de um triângulo:

C=180°−30°−45°=105°

Agora, aplicamos a Lei dos Senos:

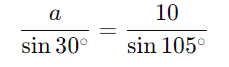
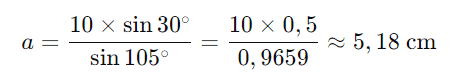
Resposta: O lado a mede aproximadamente 5,18 cm.

Lei dos Cossenos

A Lei dos Cossenos é uma generalização do Teorema de Pitágoras que pode ser aplicada a qualquer triângulo, não apenas aos triângulos retângulos. Ela relaciona os comprimentos dos lados de um triângulo com o cosseno de um de seus ângulos.

Enunciado da Lei dos Cossenos:

Em qualquer triângulo, o quadrado de um lado é igual à soma dos quadrados dos outros dois lados, menos duas vezes o produto desses lados pelo cosseno do ângulo entre eles.

Matematicamente, isso é expresso como:

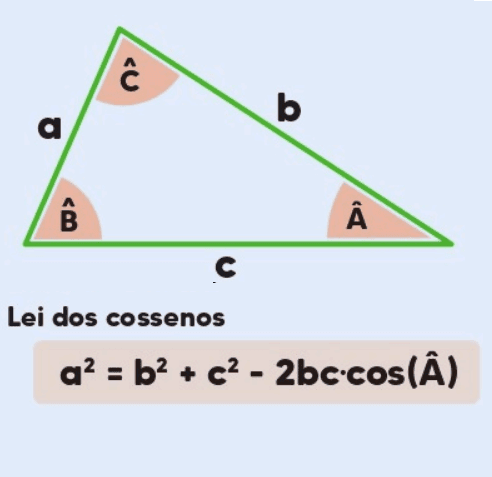
onde:

• a, b, c são os comprimentos dos lados do triângulo,
• A, B, C são os ângulos opostos a esses lados.

Aplicações da Lei dos Cossenos

A Lei dos Cossenos é especialmente útil em dois casos:

1. Quando conhecemos dois lados e o ângulo entre eles: Podemos usar a Lei dos Cossenos para calcular o terceiro lado.
2. Quando conhecemos os três lados: Podemos usar a Lei dos Cossenos para calcular qualquer um dos ângulos do triângulo.

Exemplo de Aplicação

Problema: Em um triângulo, temos a=7cm, b=10cm e C=60∘. Calcule o lado c.

Resolução: Aplicando a Lei dos Cossenos:

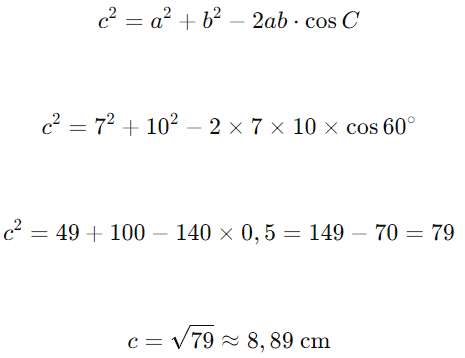
Resposta: O lado c mede aproximadamente 8,89 cm.

A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.

Exercícios Lei do Seno e Lei do Cosseno

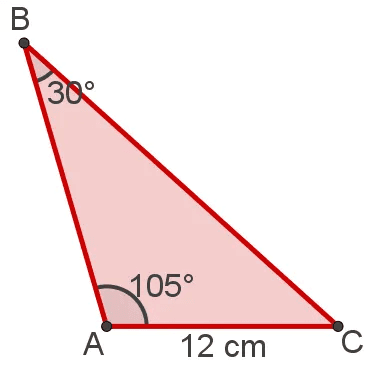
1 – (Mackenzie – SP) Três ilhas A, B e C aparecem num mapa em escala 1:10000, como na figura. Das alternativas, a que melhor se aproxima de distância entre as ilhas A e B é:

a) 2,3 km

b) 2,1 km

c) 1,9 km

d) 1,4 km

e) 1,7 km

Resposta

Observe que o segmento AB é oposto ao ângulo C. Pela soma das medidas internas de um triângulo, concluímos que o ângulo C mede 45°. Os lados que serão usados nesse problema são AC = 12 cm e AB = x. Os ângulos opostos a esses lados são: 30° e 45°, respectivamente. Na lei dos senos, temos:

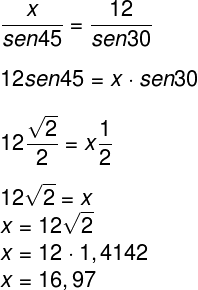
O resultado obtido está em centímetros, portanto, convertendo para metros por meio da escala e depois convertendo metros para quilômetros, teremos:

1,69 km

Como o resultado é aproximado, a alternativa correta é a letra E.

2 – Qual é a medida do lado oposto ao ângulo de 30°, em um triângulo, sabendo que os outros dois lados medem 2 e √3?

a) 1

b) 1,5

c) 2

d) 2,5

e) 3

Resposta:

Seja o lado oposto ao ângulo de 30° igual a x, podemos usar a lei dos cossenos para descobrir seu valor. Para tanto:

x² = a² + b² – 2·a·b·cosα

x² = 2² + (√3)² – 2·2·√3·cos30

x² = 4 + 3 – 2·2·√3·√3/2

x² = 7 – 4·3/2

x² = 7 – 12/2

x² = 7 – 6

x² = 1

x = 1

O lado oposto ao ângulo de 30° mede 1. Gabarito: Letra A.

Conclusão

A Lei dos Senos e a Lei dos Cossenos são ferramentas poderosas na trigonometria, permitindo resolver uma ampla variedade de problemas envolvendo triângulos. Enquanto a Lei dos Senos é particularmente útil para triângulos onde conhecemos ângulos e lados opostos, a Lei dos Cossenos é essencial quando lidamos com triângulos onde conhecemos os lados e os ângulos entre eles. Ambas as leis expandem as possibilidades de aplicação da trigonometria além dos triângulos retângulos, tornando-as indispensáveis em diversas áreas da matemática, engenharia e ciências aplicadas.

Leia também

Área de Triângulos: Conceitos e Cálculos

Área de Figuras Planas: Como Calcular, Exercícios Resolvidos

Área de Circunferências: Explorando Formas e Cálculos

Explorando Ângulos: Agudo, Obtuso, Reto e Raso

Retas Paralelas e Transversais

A Soma dos Ângulos em Polígonos: Internos e Externos

Tudo Sobre Triângulos: Classificação e Propriedades 

Congruência de Triângulos: Casos e Propriedades 

Teorema de Pitágoras: Conceito, Provas e Aplicações 

Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais

A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria 

Quadriláteros: Área, Perímetro e Diagonais 

Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos 

Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares

Quadriláteros Circunscritos: Teorema de Pitot

Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes 

Ângulos na Circunferência: Uma Exploração Completa