Conteúdo: Teoria de Conjuntos – Inclusão, Subconjuntos e Diagramas
Questão 7. No diagrama a seguir, \( A \), \( B \) e \( C \) são três conjuntos não vazios.
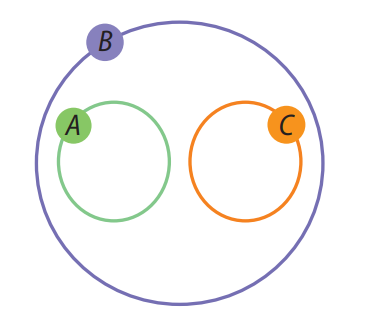
Associe V ou F a cada uma das seguintes sentenças, conforme ela seja verdadeira ou falsa:
- a) \( A \subset B \)
- b) \( C \subset B \)
- c) \( B \subset A \)
- d) \( A \subset C \)
- e) \( B \not\subset A \)
- f) \( A \subset C \)
- g) \( B \supset A \)
- h) \( A \not\supset B \)
Ver Solução
a) \( A \subset B \): V – A está totalmente dentro de B.
b) \( C \subset B \): V – C também está contido em B.
c) \( B \subset A \): F – B contém A, não o contrário.
d) \( A \subset C \): F – A e C não têm interseção visível, logo A não está dentro de C.
e) \( B \not\subset A \): V – B não está contido em A.
f) \( A \subset C \): F – Repetida da d), ainda falsa.
g) \( B \supset A \): V – Sim, B contém A.
h) \( A \not\supset B \): V – A não contém B, é o contrário.
🧠 Mapas Mentais de Matemática
























