Ângulo Excêntrico Exterior
O ângulo excêntrico exterior é um dos ângulos notáveis relacionados à circunferência. Ele aparece quando duas secantes (ou uma secante e uma tangente) se cruzam em um ponto localizado fora da circunferência.
Definição
Na figura, o ângulo \(x\) é formado pela interseção das secantes \(AB\) e \(CD\) no ponto exterior à circunferência. Esse ângulo é denominado ângulo excêntrico exterior.
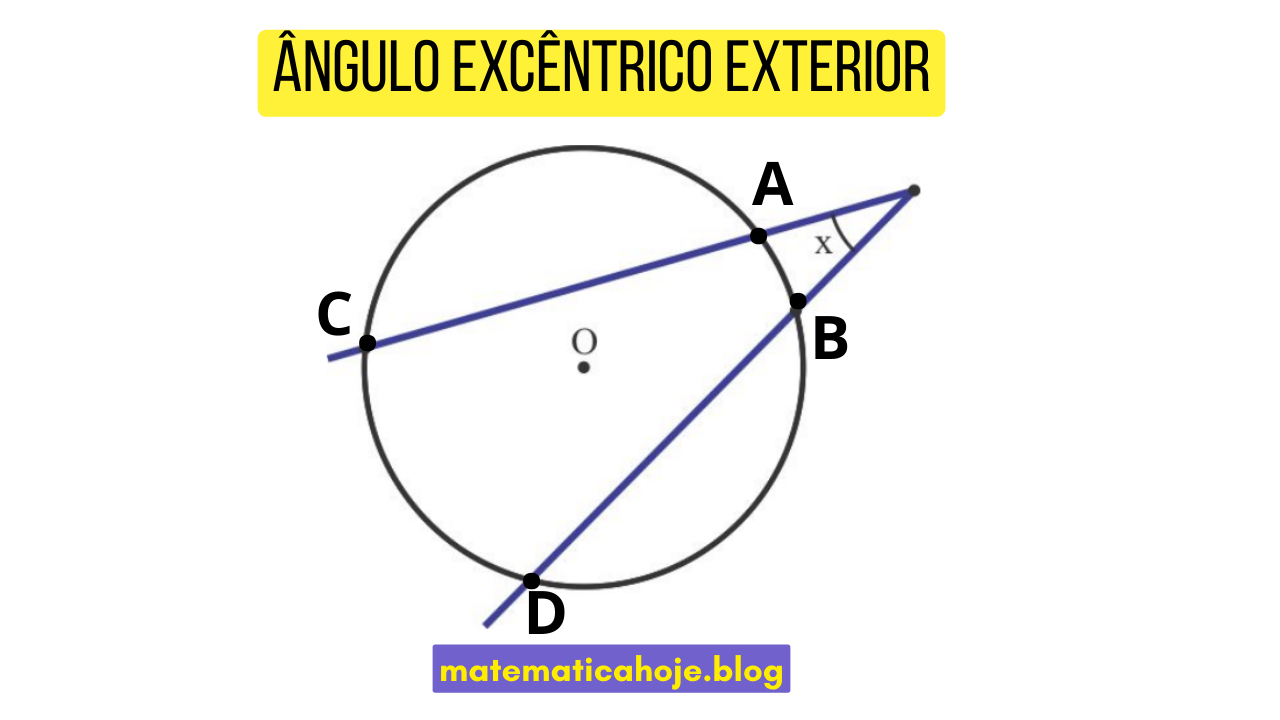
Sua medida é calculada a partir da diferença das medidas dos arcos interceptados.
Fórmula do Ângulo Excêntrico Exterior
Sejam os arcos \(\widehat{AB}\) e \(\widehat{CD}\). Então:
\(x = \tfrac{1}{2}(\widehat{AB} – \widehat{CD})\)
Ou seja, a medida do ângulo excêntrico exterior é igual à metade da diferença entre as medidas dos arcos interceptados.
Propriedades importantes
- O vértice do ângulo está sempre fora da circunferência.
- Os lados do ângulo são secantes (ou uma secante e uma tangente).
- A fórmula envolve a diferença dos arcos maiores e menores.
Exemplos resolvidos
Exemplo 1: Os arcos medem \(140^\circ\) e \(60^\circ\). Calcule o ângulo excêntrico exterior.
\(x = \tfrac{1}{2}(140^\circ – 60^\circ) = \tfrac{80^\circ}{2} = 40^\circ\).
Exemplo 2: Dois arcos medem \(200^\circ\) e \(50^\circ\). Qual o valor do ângulo?
\(x = \tfrac{1}{2}(200^\circ – 50^\circ) = \tfrac{150^\circ}{2} = 75^\circ\).
📘 Exercícios de múltipla escolha
1) Dois arcos medem \(120^\circ\) e \(40^\circ\). O ângulo excêntrico exterior mede:
- \(30^\circ\)
- \(40^\circ\)
- \(60^\circ\)
- \(80^\circ\)
Ver solução
\(x = \tfrac{1}{2}(120^\circ-40^\circ)=\tfrac{80^\circ}{2}=40^\circ\).
2) Dois arcos medem \(180^\circ\) e \(80^\circ\). O ângulo excêntrico exterior mede:
- \(40^\circ\)
- \(70^\circ\)
- \(50^\circ\)
- \(100^\circ\)
Ver solução
\(x = \tfrac{1}{2}(180^\circ-80^\circ)=\tfrac{100^\circ}{2}=50^\circ\).
3) Dois arcos medem \(210^\circ\) e \(90^\circ\). O ângulo excêntrico exterior é:
- \(50^\circ\)
- \(60^\circ\)
- \(60^\circ\)
- \(70^\circ\)
Ver solução
\(x = \tfrac{1}{2}(210^\circ-90^\circ)=\tfrac{120^\circ}{2}=60^\circ\).
Links úteis
📚 Continue estudando
O ângulo excêntrico exterior é fundamental na resolução de problemas envolvendo circunferências e arcos, sendo bastante cobrado em exames e concursos.






















