Ângulo Inscrito na Circunferência
O ângulo inscrito em uma circunferência é aquele cujo vértice pertence à circunferência e cujos lados são cordas que se encontram nesse vértice. Esse tipo de ângulo é fundamental na geometria, pois estabelece uma relação direta com o arco correspondente.
Definição
Seja uma circunferência de centro \(O\). Um ângulo inscrito é formado por dois segmentos que ligam um ponto da circunferência a outros dois pontos distintos dela.
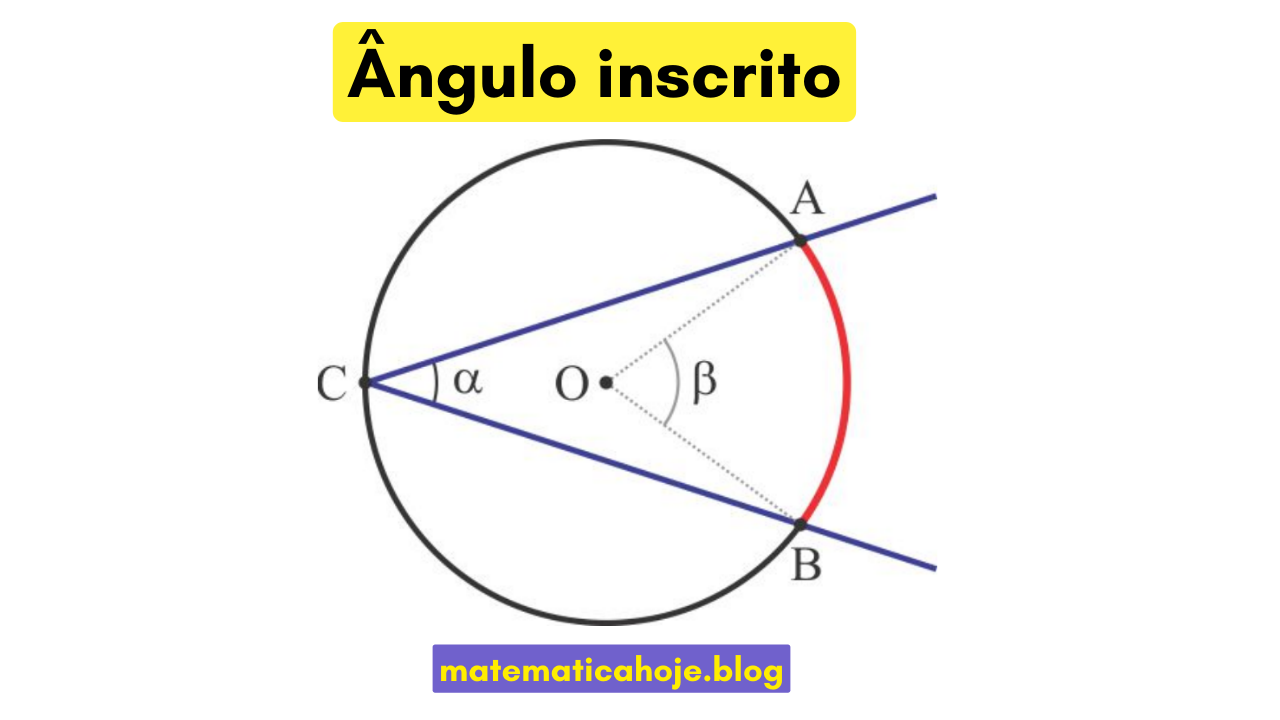
No desenho, \(\angle ACB\) é um ângulo inscrito que subentende o arco \(AB\). O arco é indicado em vermelho na figura.
Propriedade Fundamental
O valor do ângulo inscrito é sempre a metade da medida do arco correspondente. Ou seja:
\(\alpha = \tfrac{1}{2}\beta\)
Onde:
- \(\alpha\) é a medida do ângulo inscrito.
- \(\beta\) é a medida do arco correspondente ou do ângulo central que o subtende.
Casos importantes
- Se o arco vale \(180^\circ\), o ângulo inscrito correspondente mede \(90^\circ\).
- Ângulos inscritos que subtendem o mesmo arco são sempre congruentes.
- Se o vértice do ângulo inscrito é um diâmetro, o ângulo é sempre reto.
Exemplos resolvidos
Exemplo 1: Se o arco correspondente mede \(100^\circ\), qual é o valor do ângulo inscrito?
Aplicando a propriedade: \(\alpha = \tfrac{1}{2}\times 100^\circ = 50^\circ\).
Exemplo 2: O arco de um diâmetro mede \(180^\circ\). Qual o valor do ângulo inscrito?
\(\alpha = \tfrac{1}{2}\times 180^\circ = 90^\circ\). Portanto, o ângulo inscrito é reto.
📘 Exercícios de múltipla escolha
1) O arco de uma circunferência mede \(120^\circ\). O ângulo inscrito correspondente mede:
- \(120^\circ\)
- \(60^\circ\)
- \(30^\circ\)
- \(90^\circ\)
Ver solução
\(\alpha = \tfrac{1}{2}\times 120^\circ = 60^\circ\).
2) Se um ângulo inscrito mede \(45^\circ\), o arco correspondente mede:
- \(45^\circ\)
- \(90^\circ\)
- \(180^\circ\)
- \(135^\circ\)
Ver solução
\(\beta = 2 \times 45^\circ = 90^\circ\).
3) Um ângulo inscrito é reto. Isso significa que o arco correspondente mede:
- \(45^\circ\)
- \(90^\circ\)
- \(180^\circ\)
- \(360^\circ\)
Ver solução
Se \(\alpha = 90^\circ\), então o arco correspondente é \(\beta = 180^\circ\).
Links úteis
📚 Continue estudando
O estudo do ângulo inscrito ajuda a compreender propriedades fundamentais da circunferência, muito cobradas em vestibulares e concursos.






















