📖 Leia Também
Descubra tudo sobre ângulos de 30°, 45° e 60° e aprenda as principais razões trigonométricas de forma simples e objetiva.
Um barco parte de A para atravessar um rio. A direção de seu deslocamento forma um ângulo de \( 120^\circ \) com a margem do rio, conforme a figura. Sendo a largura do rio \( 60 \, \text{m} \), qual é a distância \( AB \) percorrida pelo barco?
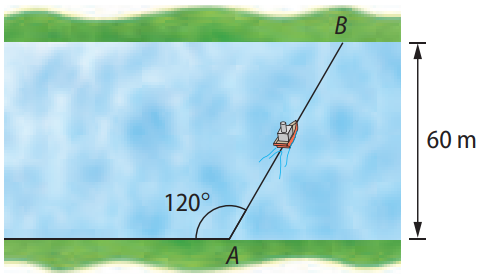
Observando o esquema, percebemos que o ângulo \( \widehat{BAC} \) é de \( 60^\circ \). Assim:
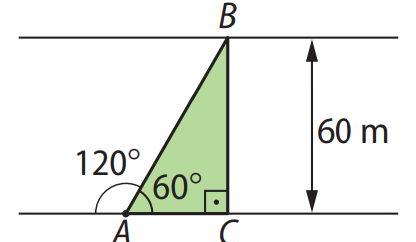
Dessa forma, a distância percorrida pelo barco é \( 40 \sqrt{3} \, \text{m} \).
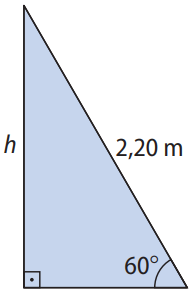
Uma escada, que mede \( 2,20 \, \text{m} \) de comprimento, acha-se apoiada em uma parede vertical e forma um ângulo de \( 60^\circ \) com o plano horizontal. Determine a que altura o topo da escada se encontra do chão. Adote \( \sqrt{3} = 1,73 \).
Usando o triângulo formado pela escada, podemos escrever:
Substituindo \( \sqrt{3} = 1,73 \), temos:
Portanto, o topo da escada está a \( 1,903 \, \text{m} \) de altura do chão.
Uma torre vertical de \( 12 \, \text{m} \) de altura é vista sob um ângulo de \( 30^\circ \) por uma pessoa que se encontra a uma distância \( x \) do centro de sua base. O plano da base da torre está no nível dos olhos do observador. Determine a distância \( x \). Adote \( \tan 30^\circ = 0,58 \).
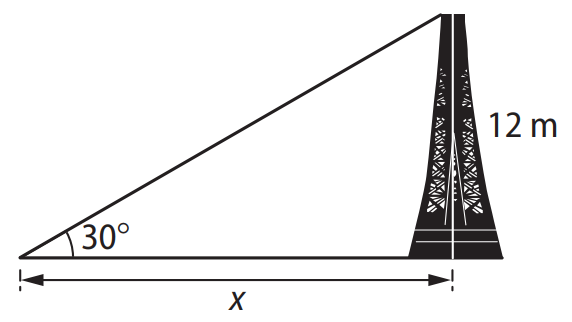
Usando a definição de tangente no triângulo formado, temos:
Portanto, a distância \( x \) é aproximadamente \( 20,7 \, \text{m} \).
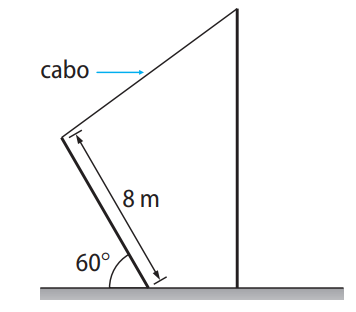
(UFG-GO) Para dar sustentação a um poste telefônico, utilizou-se um outro poste com \( 8 \, \text{m} \) de comprimento, fixado ao solo a \( 4 \, \text{m} \) de distância do poste telefônico, inclinado sob um ângulo de \( 60^\circ \), conforme a figura abaixo.
Considerando-se que foram utilizados \( 10 \, \text{m} \) de cabo para ligar os dois postes, determine a altura do poste telefônico em relação ao solo.
Segundo o enunciado, temos: \( BA = 8 \, \text{m} \), \( DA = 4 \, \text{m} \) e \( BC = 10 \, \text{m} \).
Considerando-se \( DE = BF = y \) e \( BE = x + 4 \), podemos resolver da seguinte forma:
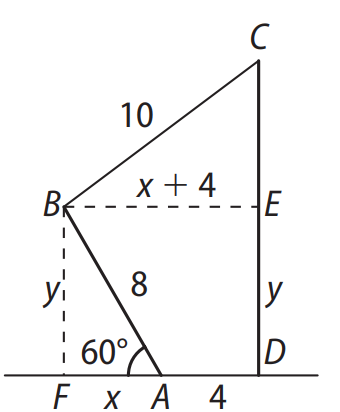
Aplicando o Teorema de Pitágoras no triângulo \( CEB \):
Assim, a altura do poste é:
Portanto, a altura do poste telefônico em relação ao solo é \( 6 + 4\sqrt{3} \, \text{m} \).
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon
No triângulo \( ABC \) a seguir, \( CH \) é a altura relativa ao lado \( AB \).
Determine:
a) a medida de \( CH \). Adote \( \tan 30^\circ = \frac{\sqrt{3}}{3} \).
b) a medida do ângulo \( \widehat{BAC} \).
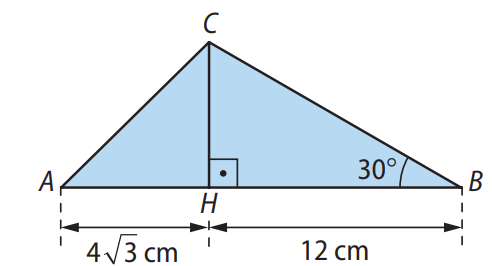
a) Para determinar a medida de \( CH \), aplicamos a definição de tangente:
Portanto, a medida de \( CH \) é \( 4\sqrt{3} \, \text{cm} \).
b) Para determinar o ângulo \( \widehat{BAC} \), usamos:
Portanto, \( \widehat{BAC} = 45^\circ \).
(IFSC) A ilustração a seguir representa a planta das ruas de uma cidade. A rua representada pelo segmento \( BC \) tem 50 m de comprimento.
Um dos engenheiros do projeto de pavimentação dessas ruas esqueceu de indicar algumas distâncias.
Considerando que um de seus técnicos efetuou os cálculos, é CORRETO afirmar que o total de metros da rua que vai do ponto \( A \) até o ponto \( D \) é de:
a) \( 50 \sqrt{3} \, \text{m} \)
b) \( 150 \sqrt{3} \, \text{m} \)
c) \( 50 \, \text{m} \)
d) \( 100 \, \text{m} \)
e) \( 100 \sqrt{3} \, \text{m} \)
Sabendo que o segmento \( BC \) mede 50 m, determinamos a medida de \( AB \) usando tangente:
Com a medida de \( AB \) calculada, determinamos \( AD \) em metros:
Resposta correta: alternativa e.
(Fuvest-SP) No quadrilátero \( ABCD \) da figura abaixo, \( E \) é um ponto sobre o lado \( AD \) tal que o ângulo \( \widehat{A \hat{B} E} \) mede \( 60^\circ \) e os ângulos \( \widehat{E \hat{B} C} \) e \( \widehat{B \hat{C} D} \) são retos. Sabe-se ainda que \( AB = CD = \sqrt{3} \, \text{m} \) e \( BC = 1 \, \text{m} \). Determine a medida de \( AD \).
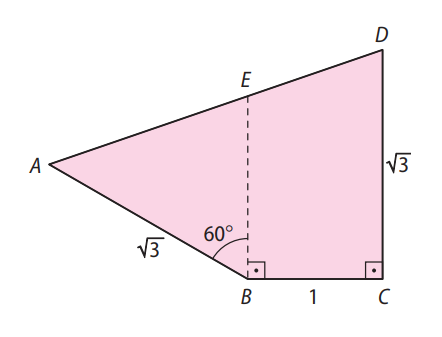
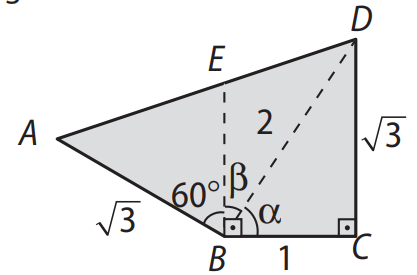
Utilizando o segmento auxiliar \( BD \), divide-se o quadrilátero nos triângulos \( DCB \) e \( ABD \).
1) Triângulo \( DCB \):
Como \( \sin \alpha = \frac{DC}{BD} = \frac{\sqrt{3}}{2} \), temos \( \alpha = 60^\circ \) e, portanto, \( \beta = 30^\circ \).
2) Triângulo \( ABD \):
Portanto, a medida de \( AD \) é \( \sqrt{7} \, \text{m} \).
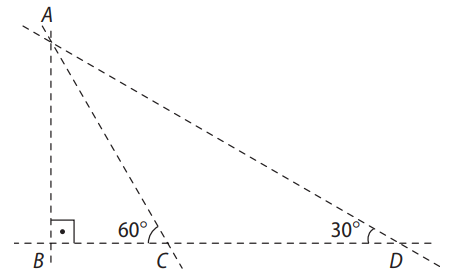
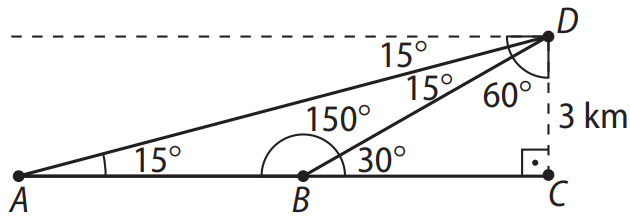
(UFV-MG) Um passageiro em um avião avista duas cidades, \( A \) e \( B \), sob ângulos de \( 15^\circ \) e \( 30^\circ \), respectivamente, conforme a figura a seguir.
Se o avião está a uma altitude de \( 3 \, \text{km} \), a distância entre as cidades \( A \) e \( B \) é:

a) 7 km.
b) 5,5 km.
c) 5 km.
d) 6,5 km.
e) 6 km.
Observando o esquema, nota-se que os ângulos \( \widehat{A \hat{D} B} \) e \( \widehat{D \hat{A} B} \) medem \( 15^\circ \). Assim, o triângulo \( DAB \) é isósceles, e a distância entre as cidades \( A \) e \( B \) é igual a \( BD \).
Para encontrar \( BD \), temos:
Portanto, a distância entre as cidades \( A \) e \( B \) é 6 km (alternativa e).
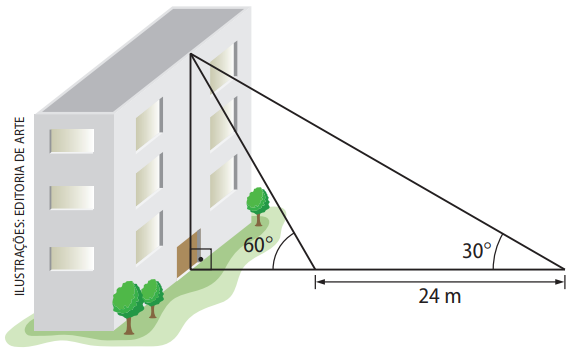
A partir de um ponto, observa-se o topo de um prédio sob um ângulo de \( 30^\circ \).
Caminhando 24 m em direção ao prédio, atinge-se outro ponto, de onde se vê o topo do prédio segundo um ângulo de \( 60^\circ \).
Desprezando a altura do observador, calcule, em metro, a altura do prédio.
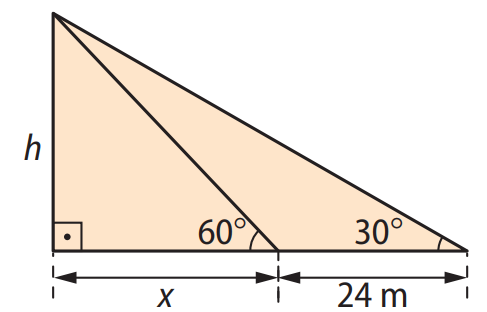
Seja \( h \) a altura do prédio e \( x \) a distância do ponto mais próximo ao prédio. Temos os seguintes sistemas de equações:
Substituindo \( x \) da equação (I) na (II):
Portanto, a altura do prédio é \( 12 \sqrt{3} \, \text{m} \).
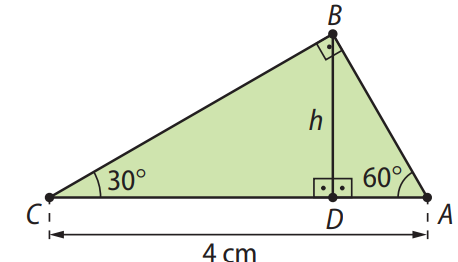
(UECE) As medidas dos ângulos internos de um triângulo são respectivamente \( 30^\circ, 60^\circ \) e \( 90^\circ \). Se a medida do maior lado deste triângulo é \( 4 \, \text{cm} \), então, a medida em cm da altura relativa a este lado é:
a) \( \sqrt{2} \)
b) \( \sqrt{6} \)
c) \( \sqrt{3} \)
d) \( \sqrt{5} \)
Seja \( h \) a altura procurada. De acordo com o triângulo, temos:
De (I) e (II), obtemos:
Sabendo que \( AD + DC = AC = 4 \), temos:
Substituindo \( AD \) em (I):
Resposta correta: alternativa c.
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
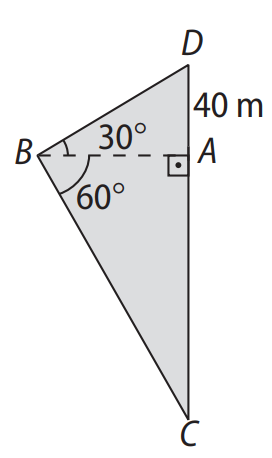
🔗 Acesse na Amazon(Unicamp-SP) Para medir a largura \( AC \) de um rio, um homem utilizou o seguinte procedimento: localizou um ponto \( B \) de onde podia ver na margem oposta o coqueiro \( C \), de forma que o ângulo \( \widehat{A \hat{B} C} \) fosse \( 60^\circ \); determinou o ponto \( D \) no prolongamento de \( CA \), de forma que o ângulo \( \widehat{C \hat{B} D} \) fosse \( 90^\circ \). Medindo \( AD = 40 \, \text{m} \), ache a largura do rio \( AC \).
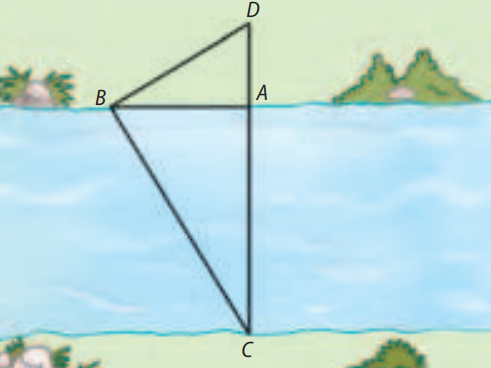
No triângulo \( BAD \), aplicando a tangente de \( 30^\circ \):
Para encontrar a largura do rio \( AC \), que é cateto do triângulo \( BAC \), usamos:
Portanto, a largura do rio é \( 120 \, \text{m} \).
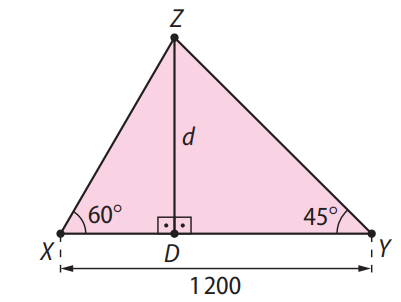
(UECE) José caminhou na praia em linha reta deslocando-se do ponto \( X \) ao ponto \( Y \), percorrendo um total de \( 1200 \, \text{m} \). No ponto \( X \), observou um navio ancorado no ponto \( Z \), de tal forma que o ângulo \( \widehat{Y \hat{X} Z} \) era aproximadamente \( 60^\circ \). Ao chegar ao ponto \( Y \), verificou que o ângulo \( \widehat{X \hat{Y} Z} \) era de \( 45^\circ \). Nessas condições, a distância do navio à praia, em metros, é aproximadamente:
a) 720.
b) 760.
c) 780.
d) 740.
Nota: Considere \( \tan 60^\circ \approx \frac{19}{11} \).
Seja \( d \) a distância entre o navio e a praia. No triângulo \( XZD \):
No triângulo \( YZD \), com ângulo de \( 45^\circ \):
Sabemos que \( XD + DY = XY = 1200 \). De (I) e (II):
Substituindo \( XD \) em (I):
Portanto, a distância do navio à praia é 760 m (alternativa b).
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon📖 Leia Também
Descubra tudo sobre ângulos de 30°, 45° e 60° e aprenda as principais razões trigonométricas de forma simples e objetiva.