Ângulos Excêntricos na Circunferência
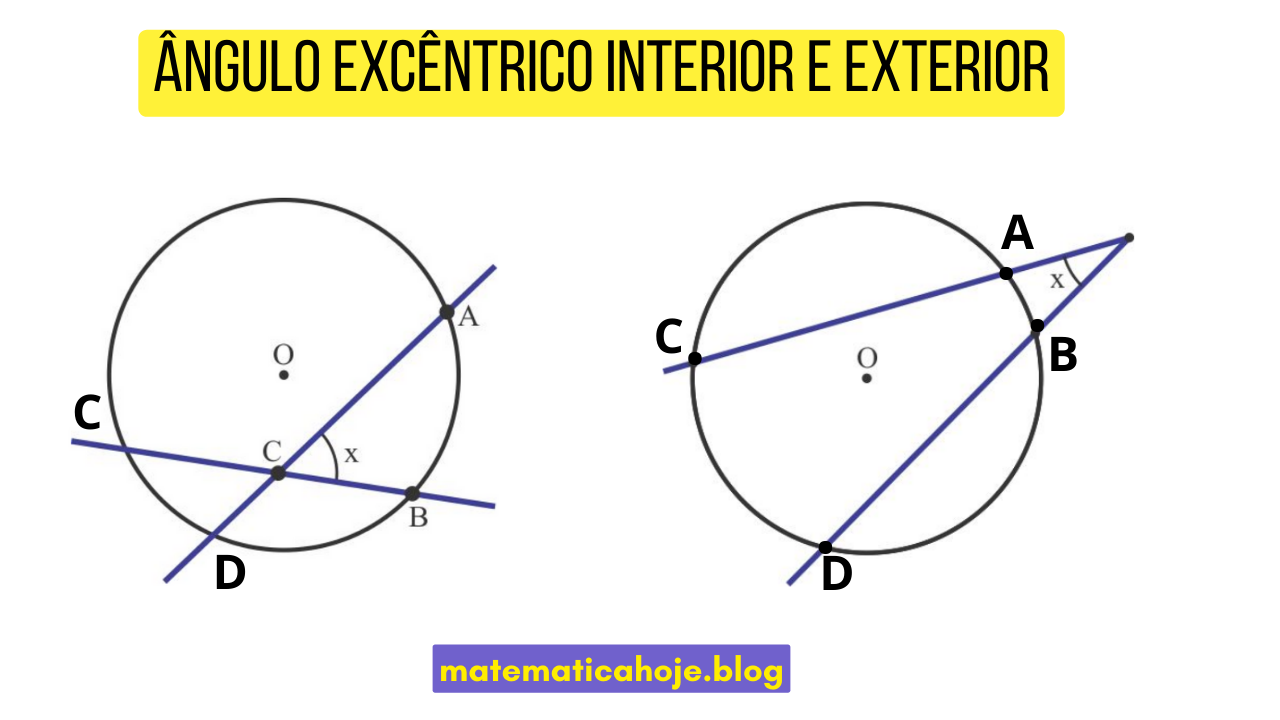
Os ângulos excêntricos são aqueles cujo vértice está fora do centro da circunferência. Eles podem ser classificados em dois tipos: ângulo excêntrico interior e ângulo excêntrico exterior. Ambos possuem fórmulas próprias e aparecem frequentemente em problemas de geometria.
Ângulo Excêntrico Interior
O ângulo excêntrico interior ocorre quando duas cordas se cruzam dentro da circunferência, mas fora do seu centro. O vértice do ângulo está dentro do círculo, e seus lados passam por pontos da circunferência.
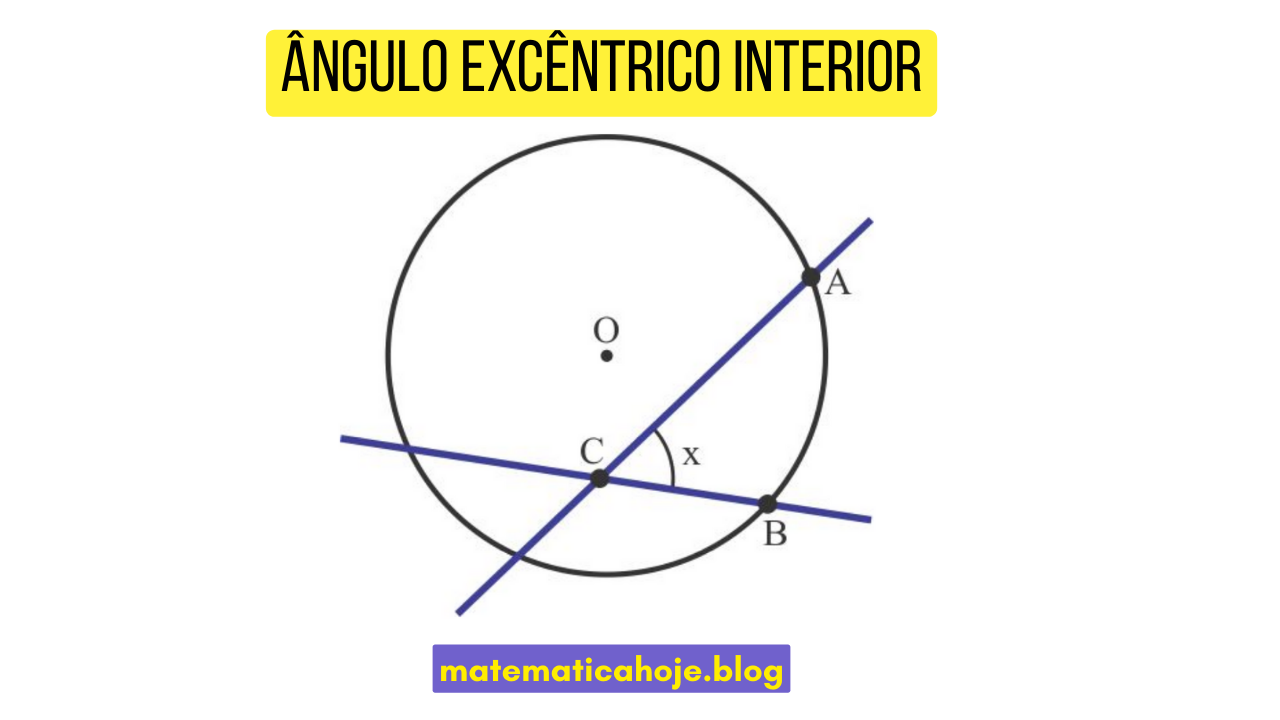
A medida do ângulo é a semissoma dos arcos interceptados.
\( x = \tfrac{1}{2}(\widehat{AB} + \widehat{CD}) \)
Ângulo Excêntrico Exterior
O ângulo excêntrico exterior aparece quando duas secantes (ou uma secante e uma tangente) se cruzam em um ponto fora da circunferência. O vértice está, portanto, no exterior do círculo.
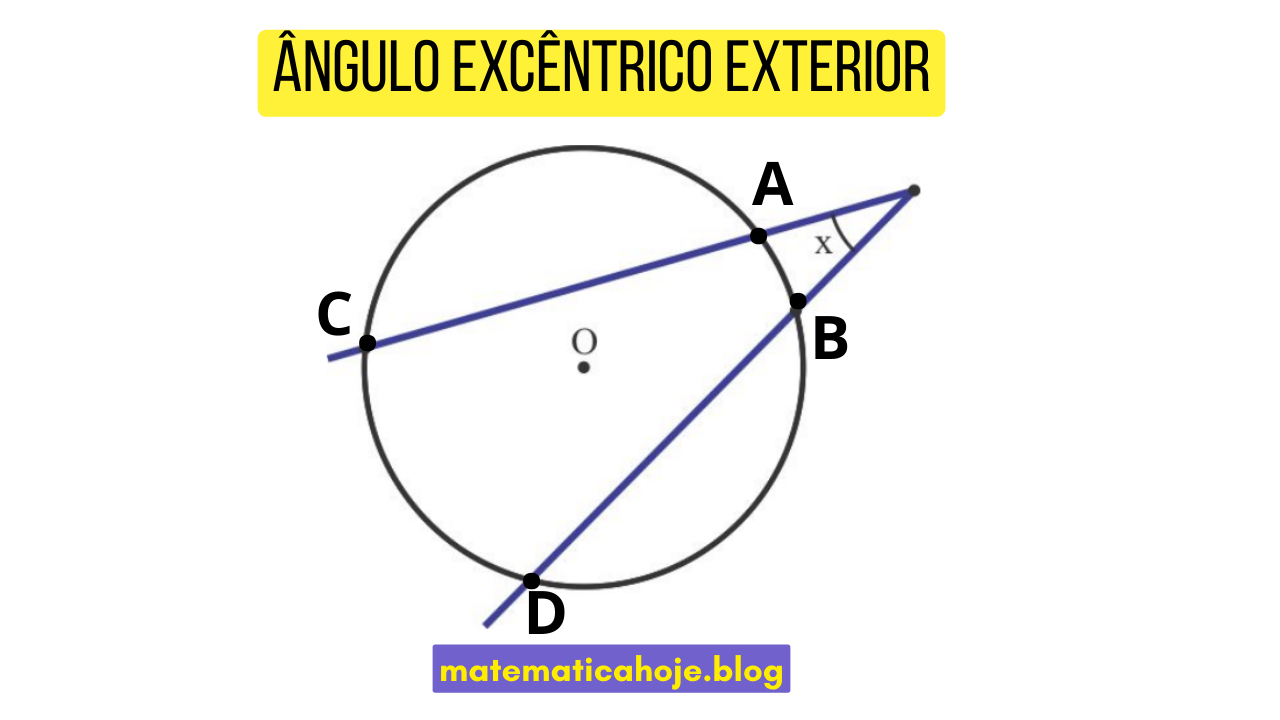
A medida do ângulo é a semidiferença dos arcos interceptados.
\( x = \tfrac{1}{2}(\widehat{AB} – \widehat{CD}) \)
Exemplos resolvidos
Exemplo 1: Ângulo Excêntrico Interior
Se os arcos medem \(100^\circ\) e \(80^\circ\), temos:
\(x = \tfrac{1}{2}(100^\circ + 80^\circ) = \tfrac{180^\circ}{2} = 90^\circ\).
Exemplo 2: Ângulo Excêntrico Exterior
Se os arcos medem \(200^\circ\) e \(50^\circ\), temos:
\(x = \tfrac{1}{2}(200^\circ – 50^\circ) = \tfrac{150^\circ}{2} = 75^\circ\).
📘 Exercícios de múltipla escolha
1) Dois arcos medem \(140^\circ\) e \(80^\circ\). O ângulo excêntrico interior é:
- \(90^\circ\)
- \(100^\circ\)
- \(110^\circ\)
- \(120^\circ\)
Ver solução
\(x=\tfrac{1}{2}(140^\circ+80^\circ)=\tfrac{220^\circ}{2}=110^\circ\).
2) Dois arcos medem \(160^\circ\) e \(40^\circ\). O ângulo excêntrico exterior é:
- \(40^\circ\)
- \(50^\circ\)
- \(60^\circ\)
- \(60^\circ\)
Ver solução
\(x=\tfrac{1}{2}(160^\circ-40^\circ)=\tfrac{120^\circ}{2}=60^\circ\).
3) Os arcos medem \(220^\circ\) e \(100^\circ\). O ângulo excêntrico interior é:
- \(140^\circ\)
- \(160^\circ\)
- \(180^\circ\)
- \(200^\circ\)
Ver solução
\(x=\tfrac{1}{2}(220^\circ+100^\circ)=\tfrac{320^\circ}{2}=160^\circ\).
Links úteis
📚 Continue estudando
Os ângulos excêntricos são fundamentais na geometria da circunferência e aparecem com frequência em provas e concursos.






















