Área da coroa circular (anel)
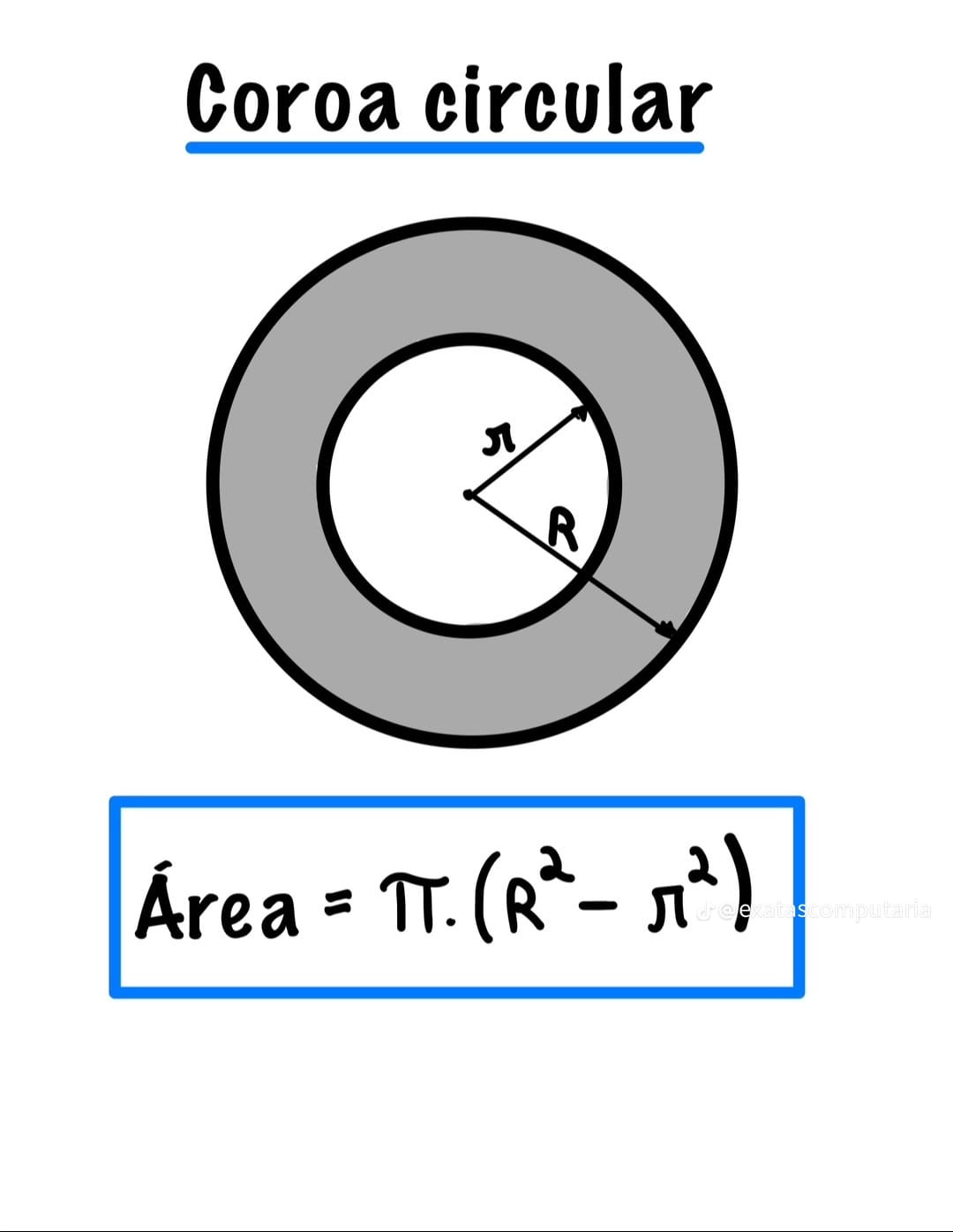
A coroa circular é a região entre dois círculos concêntricos de raios \(R\) (externo) e \(r\) (interno). Neste guia, você aprende a fórmula principal, variações úteis com diâmetros e espessura, além de exemplos resolvidos e exercícios com gabarito.
Reforce conexões: Área e comprimento da circunferência • Setor circular • eBook Fórmulas Matemática • Banco de Questões
Fórmulas essenciais
Principal
\[ A=\pi\,(R^2-r^2) \]
Cuidado: \(R\) é o raio externo; \(r\) é o interno.
Com diâmetros
\[ A=\frac{\pi}{4}\,(D^2-d^2)\quad\text{onde }D=2R,\; d=2r \]
Com espessura \(t\)
\[ t=R-r,\qquad A=\pi\,[R^2-(R-t)^2]=\pi\,t(2R-t)=\pi\,t(2r+t) \]
Útil quando a peça é “um disco com furo de espessura \(t\)”.
Comprimento das bordas
\[ C_{\text{externa}}=2\pi R,\qquad C_{\text{interna}}=2\pi r \]
Às vezes o problema fornece os perímetros para você recuperar \(R\) e \(r\).
Para revisar, consulte: circunferência e setor circular.
📘 Fórmulas sempre à mão
Tenha as expressões mais usadas de Geometria (círculo, setor, anel, polígonos, trigonometria…) no eBook Fórmulas Matemática.
Exemplos resolvidos
Exemplo 1 raios dados
Calcule a área da coroa circular com \(R=10\,\text{cm}\) e \(r=6\,\text{cm}\). Use \(\pi\approx3{,}14\).
Ver solução
\(=\pi(10^2-6^2)\)
\(=\pi(100-36)=64\pi\)
\(\approx 64\cdot 3{,}14=200{,}96\approx 201{,}0\,\text{cm}^2\).
Exemplo 2 achar o furo
Uma chapa circular de raio externo \(R=10\,\text{cm}\) possui área de anel \(A=75\pi\,\text{cm}^2\). Determine o raio interno \(r\).
Ver solução
\(=10^2-75=25\)
\(r=\sqrt{25}=5\,\text{cm}\).
Exemplo 3 com espessura
Um anel tem espessura \(t=2\,\text{cm}\) e raio interno \(r=8\,\text{cm}\). Encontre a área.
Ver solução
\(=\pi\cdot 2\cdot (16+2)\)
\(=36\pi\,\text{cm}^2\).
Exemplo 4 usando diâmetros
Para \(D=30\,\text{cm}\) e \(d=18\,\text{cm}\), calcule a área da coroa circular.
Ver solução
\(=\dfrac{\pi}{4}(900-324)\)
\(=\dfrac{\pi}{4}\cdot 576\)
\(=144\pi\,\text{cm}^2\).
Exercícios de múltipla escolha (com gabarito)
Enunciados claros e soluções com os passos um abaixo do outro após cada “=”.
1) Para \(R=7\) e \(r=3\) (em cm), a área do anel é:
Gabarito e solução
\(=\pi\cdot 40=40\pi\Rightarrow\) Letra C.
2) Sabendo que \(A=108\pi\) e \(R=12\), o raio interno \(r\) é:
Gabarito e solução
\(r^2=36\Rightarrow r=6\Rightarrow\) Letra B.
3) Um anel possui raio externo \(R=12\) e espessura \(t=5\). A área é:
Gabarito e solução
\(=5\cdot 19\pi=95\pi\Rightarrow\) Letra C.
4) Para \(D=20\) e \(d=16\), a área da coroa circular é:
Gabarito e solução
\(=\frac{\pi}{4}\cdot 144=36\pi\Rightarrow\) Letra C.
5) Um disco de raio \(10\) recebe um furo de raio \(4\). A porcentagem de área removida é:
Gabarito e solução
Área original \(=\pi\cdot 10^2=100\pi\)
\(\%\text{removida}=\dfrac{16\pi}{100\pi}\cdot 100\%=16\%\Rightarrow\) Letra B.
6) Uma arruela tem \(R=9\,\text{cm}\) e \(r=5\,\text{cm}\). A densidade superficial é \(0{,}8\,\text{g/cm}^2\). A massa é (aprox.):
Gabarito e solução
Massa \(=0{,}8\cdot 56\pi=44{,}8\pi\)
\(\approx 44{,}8\cdot 3{,}14\approx 140{,}7\approx 141\,\text{g}\Rightarrow\) Letra B.
7) Se \(A=50\pi\) e \(r=5\), a espessura \(t\) (em cm) é:
Gabarito e solução
\(t^2+10t-50=0\Rightarrow t=\frac{-10+\sqrt{100+200}}{2}\)
\(=\frac{-10+\sqrt{300}}{2}=-5+5\sqrt{3}\)
\(\approx 3{,}66\Rightarrow\) Letra C.
8) Se \(R=2r\), então \(A\) vale:
Gabarito e solução
\(=\pi(4r^2-r^2)=3\pi r^2\Rightarrow\) Letra C.
Dicas finais
- Quando o enunciado falar em “furo” ou “arruela”, pense logo em \(A=\pi(R^2-r^2)\).
- Diâmetros conhecidos? Use \(A=\frac{\pi}{4}(D^2-d^2)\) para evitar dividir por 2 várias vezes.
- Com espessura \(t\): \(A=\pi\,t(2R-t)=\pi\,t(2r+t)\) é mais rápido.













