Área do Setor Circular

Área do Setor Circular — fórmulas, exemplos e exercícios

Área do Setor Circular

O setor circular é a “fatia de pizza” do círculo, delimitada por dois raios e um arco. A área depende do raio e do ângulo central (em graus ou radianos).

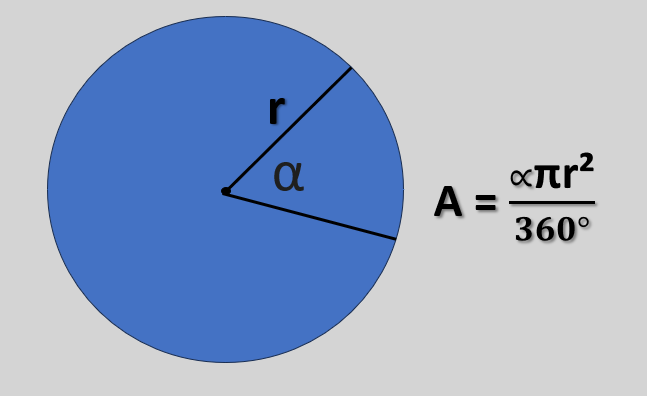
Setor circular com raio r e ângulo central α; fórmula A = απ r² / 360°
Setor de raio \(r\) e ângulo central \(\alpha\) (graus). Em radianos escrevemos \(\theta\).
Leituras relacionadas: Área do Círculo, Área do Triângulo, Polígonos Regulares e Lei dos Senos/Lei dos Cossenos.

Fórmulas da área

\[ \textbf{1) Ângulo em graus }(\alpha):\quad \boxed{A=\frac{\alpha}{360^\circ}\,\pi r^2} \]
\[ \textbf{2) Ângulo em radianos }(\theta):\quad \boxed{A=\frac{\theta}{2}\,r^2} \quad (\text{pois } \theta=\tfrac{2\pi\alpha}{360^\circ}) \]
\[ \textbf{3) Usando o comprimento do arco }(L):\quad \boxed{A=\frac{1}{2}\,r\,L} \quad (\text{já que } L=r\theta) \]

As três expressões são equivalentes. Escolha a que usa diretamente as informações do enunciado.

Exemplos resolvidos (situação-problema)

1

Setor em graus

Um logotipo ocupa um setor circular de um disco de raio \(r=10\,\text{cm}\) com ângulo \(\alpha=54^\circ\).

Dados
\(r=10\,\text{cm}\), \(\alpha=54^\circ\).

Qual é a área ocupada pelo logotipo?

Ver solução
\[ \begin{aligned} A&=\frac{\alpha}{360^\circ}\,\pi r^2\\ &=\frac{54^\circ}{360^\circ}\,\pi\cdot 10^2\\ &=\frac{3}{20}\cdot 100\pi\\ &=15\pi\\ &\approx \boxed{47{,}12\ \text{cm}^2} \end{aligned} \]
2

Setor em radianos

Um jardim em forma de setor possui raio \(r=12\,\text{m}\) e ângulo \(\theta=2{,}2\ \text{rad}\).

Dados
\(r=12\,\text{m}\), \(\theta=2{,}2\ \text{rad}\).

Qual é a área do jardim?

Ver solução
\[ \begin{aligned} A&=\frac{\theta}{2}r^2\\ &=\frac{2{,}2}{2}\cdot 12^2\\ &=1{,}1\cdot 144\\ &=\boxed{158{,}4\ \text{m}^2} \end{aligned} \]
3

Descobrindo o ângulo

Em uma placa circular, a parte colorida é um setor de raio \(r=8\,\text{cm}\) cuja área é \(A=16\pi\,\text{cm}^2\).

Dados
\(r=8\,\text{cm}\), \(A=16\pi\,\text{cm}^2\).

Qual é o ângulo central \(\alpha\) (em graus)?

Ver solução
\[ \begin{aligned} A&=\frac{\alpha}{360^\circ}\pi r^2\\ 16\pi&=\frac{\alpha}{360^\circ}\pi\cdot 8^2\\ 16\pi&=\frac{\alpha}{360^\circ}\cdot 64\pi\\ \frac{\alpha}{360^\circ}&=\frac{16}{64}=\frac14\\ \alpha&=\boxed{90^\circ} \end{aligned} \]
4

Com o comprimento do arco

Um canteiro setorial tem raio \(r=15\,\text{m}\) e o arco frontal mede \(L=12\,\text{m}\).

Dados
\(r=15\,\text{m}\), \(L=12\,\text{m}\).

Qual é a área do canteiro?

Ver solução
\[ \begin{aligned} A&=\tfrac12 rL\\ &=\tfrac12\cdot 15\cdot 12\\ &=\boxed{90\ \text{m}^2} \end{aligned} \]

Erros comuns (e como evitar)

  • Confundir graus com radianos. Em graus use \(A=\frac{\alpha}{360^\circ}\pi r^2\); em radianos use \(A=\frac{\theta}{2}r^2\).
  • Trocar raio por diâmetro. Se o problema der o diâmetro \(d\), lembre-se de que \(r=d/2\). Revise em área do círculo.
  • Arco vs. ângulo. Se vier o comprimento do arco \(L\), aplique \(A=\tfrac12 rL\) (mais direto que converter para \(\theta\)).

Exercícios propostos (múltipla escolha)

1

Setor em graus

Um radar cobre um setor de raio \(r=9\,\text{cm}\) (modelo) e ângulo \(\alpha=120^\circ\).

A área do setor é:

  • A) \(18\pi\ \text{cm}^2\)
  • B) \( \mathbf{27\pi\ \text{cm}^2\ (\approx 84{,}82)} \)
  • C) \(36\pi\ \text{cm}^2\)
  • D) \(81\pi\ \text{cm}^2\)
Gabarito
\[ A=\frac{120^\circ}{360^\circ}\pi\cdot 9^2=\frac13\cdot 81\pi=\boxed{27\pi\ \text{cm}^2} \]
2

Setor em radianos

Um refletor ilumina um setor de raio \(r=5\,\text{m}\) com abertura \(\theta=1{,}6\ \text{rad}\).

A área iluminada é:

  • A) \(12{,}5\ \text{m}^2\)
  • B) \( \mathbf{20\ \text{m}^2} \)
  • C) \(25\ \text{m}^2\)
  • D) \(40\ \text{m}^2\)
Gabarito
\[ A=\frac{\theta}{2}r^2=\frac{1{,}6}{2}\cdot 25=\boxed{20\ \text{m}^2} \]
3

Descobrindo o raio

Uma placa setorial tem área \(A=50\pi\,\text{cm}^2\) e ângulo \(\alpha=100^\circ\).

O raio da placa é:

  • A) \(10{,}00\ \text{cm}\)
  • B) \( \mathbf{13{,}42\ \text{cm}} \)
  • C) \(15{,}00\ \text{cm}\)
  • D) \(18{,}00\ \text{cm}\)
Gabarito
\[ \begin{aligned} A&=\frac{\alpha}{360^\circ}\pi r^2\\ 50\pi&=\frac{100^\circ}{360^\circ}\pi r^2\\ r^2&=\frac{360\cdot 50}{100}=180\\ r&=\sqrt{180}\approx \boxed{13{,}42\ \text{cm}} \end{aligned} \]
4

Com o arco

Um jardim setorial tem área \(A=63\,\text{m}^2\) e raio \(r=14\,\text{m}\).

O comprimento do arco frontal é:

  • A) \(7\ \text{m}\)
  • B) \( \mathbf{9\ \text{m}} \)
  • C) \(12\ \text{m}\)
  • D) \(18\ \text{m}\)
Gabarito
\[ A=\tfrac12 rL \Rightarrow L=\frac{2A}{r}=\frac{2\cdot 63}{14}=\boxed{9\ \text{m}} \]

Veja também: área do círculo (fórmulas equivalentes) e área do triângulo (útil em segmentos circulares).

Materiais do Matemática Hoje

Relacionadas

Igualdade entre pares de ângulos opostos no Triângulo

Como calcular a área de um setor circular

Ângulo Obtuso

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube