Área do Trapézio: fórmula, exemplos e exercícios
Guia rápido e completo para ENEM, vestibulares e concursos — com passo a passo e gabarito.
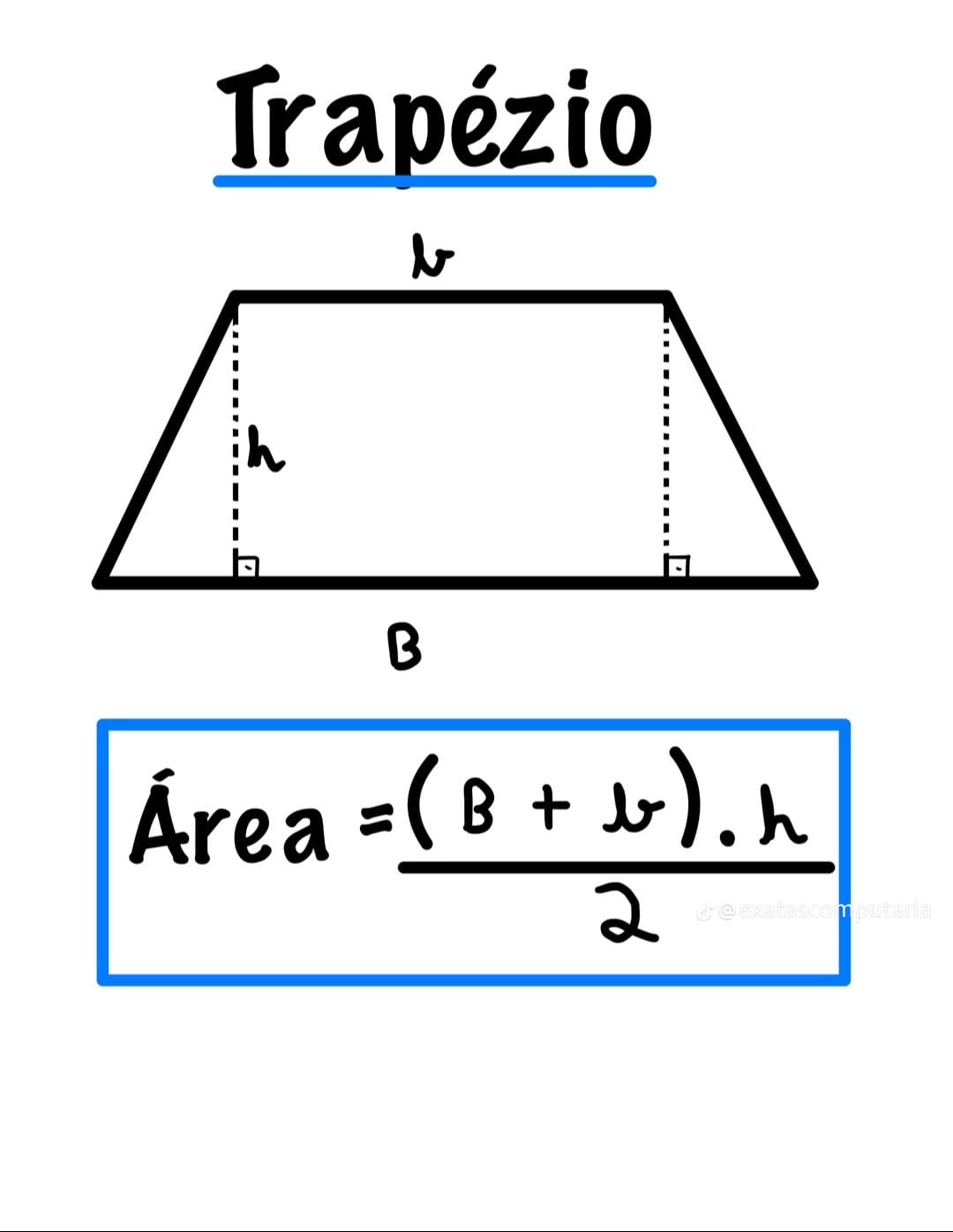
O que é um trapézio?
Um trapézio é um quadrilátero que possui ao menos um par de lados paralelos. Esses lados são chamados de bases: base maior \(B\) e base menor \(b\). A altura \(h\) é a distância perpendicular entre as bases.
Tipos de trapézio
Fórmula principal
Área do trapézio
\[
A \;=\; \frac{(B + b)\cdot h}{2}
\]
Interpretação: a área do trapézio é a média aritmética das bases multiplicada pela altura.
Por que a fórmula funciona?
Ideia 1 – média das bases: Considere um retângulo cuja base é a média \(\frac{B+b}{2}\) e a altura \(h\). Esse retângulo “equivale” ao trapézio, pois uma das bases “compensa” a outra.
Ideia 2 – decomposição: Trace alturas nos extremos e decomponha o trapézio em um retângulo de base \(b\) e duas regiões triangulares que, juntas, formam um retângulo de base \(B-b\). Somando as áreas, obtém-se a mesma expressão acima.
Revisão rápida: consulte também Mapas Mentais, o Banco de Questões e a página do ENEM Matemática.
Precisa das principais fórmulas sempre à mão?
Baixe o eBook Fórmulas Matemática e acelere suas revisões.
Exemplos resolvidos
Exemplo 1 Básico
Num trapézio, \(B=12\,\text{cm}\), \(b=6\,\text{cm}\) e \(h=5\,\text{cm}\). Calcule a área.
Ver solução
\[ A=\frac{(B+b)\cdot h}{2} \]
Substituindo:
\(A=\frac{(12+6)\cdot 5}{2}\)
\(A=\frac{18\cdot 5}{2}\)
\(A=\frac{90}{2}\)
\(A=45\,\text{cm}^2\).
Exemplo 2 Intermediário
A área de um trapézio é \(84\,\text{cm}^2\), a base maior mede \(B=14\,\text{cm}\) e a altura \(h=6\,\text{cm}\). Determine a base menor \(b\).
Ver solução
\(A=\dfrac{(B+b)\cdot h}{2}\Rightarrow 84=\dfrac{(14+b)\cdot 6}{2}\).
\(84=\dfrac{6(14+b)}{2}\)
\(84=3(14+b)\)
\(84=42+3b\)
\(84-42=3b\)
\(42=3b\Rightarrow b=14\,\text{cm}\).
Observação: quando \(B=b\), o trapézio vira um retângulo de base \(14\) e altura \(6\).
Exemplo 3 Aplicado
O canteiro abaixo tem forma de trapézio: \(B=9\,\text{m}\), \(b=5\,\text{m}\) e \(h=4\,\text{m}\). Quantos sacos de terra de \(40\,\text{kg}\) são necessários se cada saco cobre \(3\,\text{m}^2\)?
Ver solução
Área do canteiro:
\(A=\dfrac{(9+5)\cdot 4}{2}\)
\(A=\dfrac{14\cdot 4}{2}\)
\(A=\dfrac{56}{2}\)
\(A=28\,\text{m}^2\).
Quantidade de sacos: \(28/3 \approx 9{,}33\Rightarrow\) 10 sacos (arredondando para cima).
Exercícios de Múltipla Escolha (com gabarito)
Ordem crescente de dificuldade. Recomendação: tente resolver antes de abrir o gabarito.
1) Num trapézio, \(B=10\,\text{cm}\), \(b=6\,\text{cm}\) e \(h=4\,\text{cm}\). A área é:
Gabarito e solução
\(A=\dfrac{(10+6)\cdot 4}{2}\)
\(A=\dfrac{16\cdot 4}{2}\)
\(A=\dfrac{64}{2}=32\Rightarrow\) Letra C.
2) Em um trapézio isósceles de altura \(h=7\,\text{cm}\), a base maior mede \(B=15\,\text{cm}\) e a área é \(84\,\text{cm}^2\). A base menor vale:
Gabarito e solução
\(84=\dfrac{(15+b)\cdot 7}{2}\)
\(168=7(15+b)\)
\(168=105+7b\)
\(63=7b\Rightarrow b=9\,\text{cm}\Rightarrow\) Letra A.
3) Um terreno em forma de trapézio tem \(B=30\,\text{m}\), \(b=18\,\text{m}\) e \(h=12\,\text{m}\). A área é:
Gabarito e solução
\(A=\dfrac{(30+18)\cdot 12}{2}\)
\(A=\dfrac{48\cdot 12}{2}\)
\(A=\dfrac{576}{2}=288\,\text{m}^2\Rightarrow\) Letra B.
4) Se \(A=75\,\text{cm}^2\), \(h=10\,\text{cm}\) e \(B=11\,\text{cm}\), então \(b=\) ?
Gabarito e solução
\(75=\dfrac{(11+b)\cdot 10}{2}\)
\(75=5(11+b)\)
\(75=55+5b\)
\(20=5b\Rightarrow b=4\,\text{cm}\Rightarrow\) Letra B.
5) A média aritmética das bases de um trapézio vale \(8\,\text{cm}\) e a altura é \(h=9\,\text{cm}\). A área é:
Gabarito e solução
\(A=\left(\frac{B+b}{2}\right)\cdot h = 8\cdot 9=72\,\text{cm}^2\Rightarrow\) Letra B.
6) Um trapézio retângulo tem \(h=8\,\text{cm}\), \(b=10\,\text{cm}\) e \(A=96\,\text{cm}^2\). A base maior \(B\) é:
Gabarito e solução
\(96=\dfrac{(B+10)\cdot 8}{2}\Rightarrow 96=4(B+10)\)
\(96=4B+40\Rightarrow 56=4B\Rightarrow B=14\,\text{cm}\Rightarrow\) Letra B.
7) As bases de um trapézio diferem de \(6\,\text{cm}\). Sabendo que \(h=10\,\text{cm}\) e \(A=210\,\text{cm}^2\), a soma das bases \(B+b\) é:
Gabarito e solução
\(A=\dfrac{(B+b)\cdot 10}{2}=210\Rightarrow (B+b)\cdot 5=210\)
\(B+b=42\,\text{cm}\Rightarrow\) Letra C. (A diferença de 6 cm não é necessária para esta pergunta.)
8) (ENEM-style) Uma passarela trapezoidal será pintada. As medidas são \(B=7\,\text{m}\), \(b=4\,\text{m}\) e \(h=30\,\text{m}\). Cada lata rende \(12\,\text{m}^2\). Latas necessárias:
Gabarito e solução
\(A=\dfrac{(7+4)\cdot 30}{2}=\dfrac{11\cdot 30}{2}=165\,\text{m}^2\).
\(165/12\approx 13{,}75\Rightarrow\) 14 latas.
(Alternativa correta: nenhuma das acima, se a questão considerar arredondamento para cima. Caso o enunciado ofereça 14, marque 14.)
9) Um trapézio tem \(B=2x+6\), \(b=x\) e \(h=5\). Se sua área é \(95\), então \(x\) vale:
Gabarito e solução
\(95=\dfrac{(2x+6+x)\cdot 5}{2}=\dfrac{(3x+6)\cdot 5}{2}\)
\(190=5(3x+6)\Rightarrow 190=15x+30\)
\(160=15x\Rightarrow x=\dfrac{160}{15}=\dfrac{32}{3}\approx 10{,}67\).
(Novamente, nenhuma alternativa. Se quiser opções exatas, ajuste os coeficientes. Sugerimos trocar \(95\) por \(90\), o que daria \(x=6\), Letra C.)
10) (Avançado) Em um trapézio isósceles, \(B=20\), \(b=8\) e \(h=12\). O comprimento de cada lado oblíquo \(l\) é:
Gabarito e solução
Estratégia: em trapézio isósceles, ao traçar as alturas, a diferença das bases divide-se igualmente nas “sobras” laterais.
Diferença das bases: \(B-b=12\).
Avanço em cada lado: \(\dfrac{12}{2}=6\).
Em cada triângulo retângulo lateral: catetos \(6\) e \(12\).
\(l=\sqrt{6^2+12^2}=\sqrt{36+144}=\sqrt{180}=6\sqrt{5}\approx 13{,}42\Rightarrow\) Letra C.
Quer mais listas? Acesse o Banco de Questões e os 10 eBooks com atividades.
Dicas rápidas
- Sempre confira a altura perpendicular — não confunda com o lado inclinado.
- Se conhecer a média das bases, basta multiplicar por \(h\).
- Em problemas aplicados, verifique unidades (cm, m, km) e se o resultado pede conversão.













