Área do Triângulo com Seno: Fórmula Trigonométrica, Exemplos e Exercícios
Aprenda como calcular a área de um triângulo usando duas medidas de lados e o seno do ângulo entre eles.
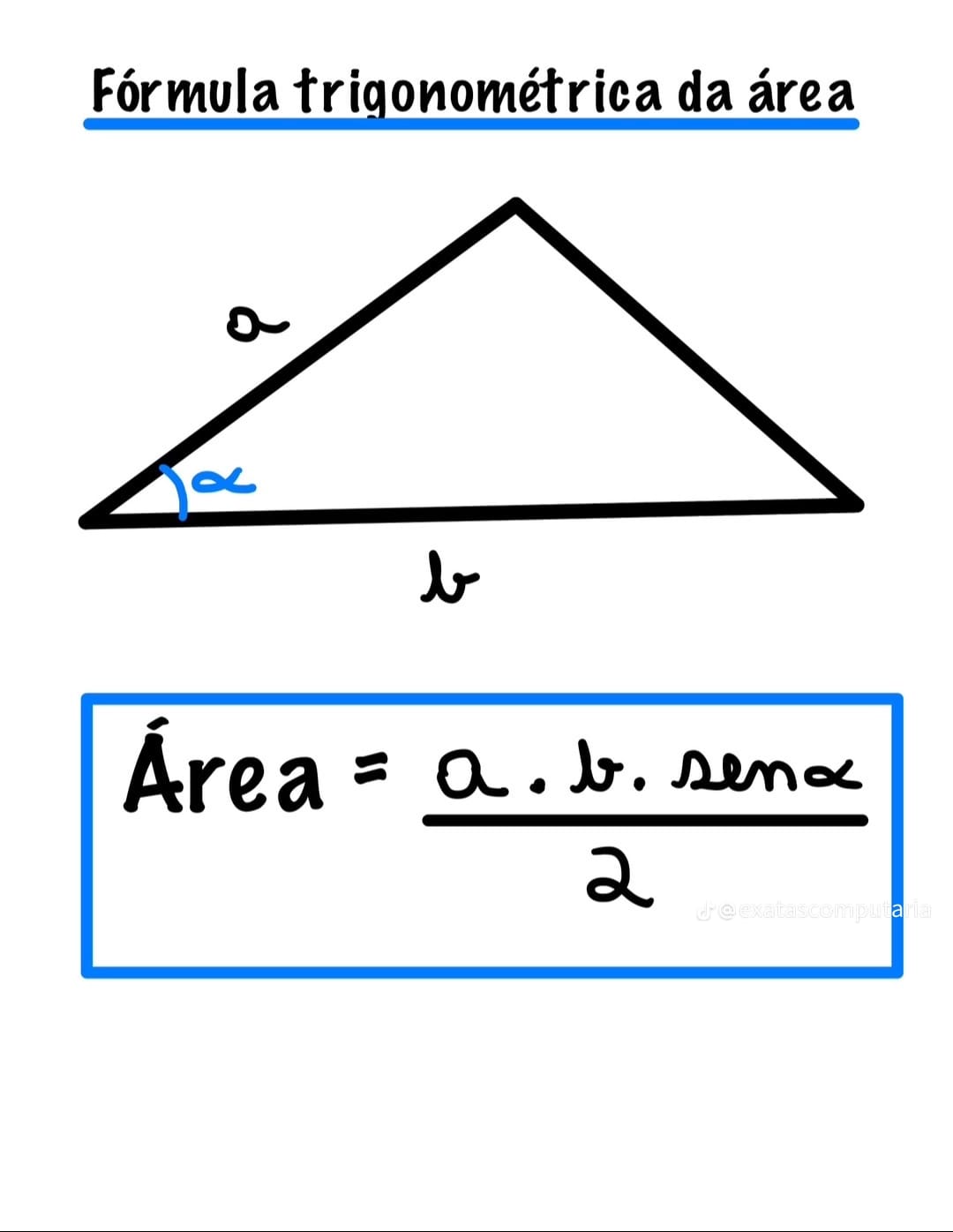
O que é a fórmula trigonométrica da área do triângulo?
A fórmula trigonométrica da área do triângulo é uma forma prática de calcular a superfície de um triângulo quando se conhecem dois lados e o ângulo formado entre eles. Essa expressão é muito usada em problemas de trigonometria, geometria plana e também em questões de vestibulares e concursos.
Seja um triângulo com lados \(a\), \(b\) e o ângulo \(\alpha\) entre eles, a área é dada por:
\[ A = \frac{a \cdot b \cdot \sin(\alpha)}{2} \]
Essa fórmula é uma alternativa à clássica expressão \(\frac{base \cdot altura}{2}\), pois o seno do ângulo já incorpora a altura implícita entre os lados.
Confira também: Mapas Mentais de Matemática | ENEM Matemática | Banco de Questões
📘 Precisa das principais fórmulas sempre à mão?
Baixe gratuitamente o eBook Fórmulas Matemática e estude com organização e clareza.
Como essa fórmula é obtida?
Sabemos que a área de um triângulo é dada por:
\[ A = \frac{base \cdot altura}{2} \]
Ao considerar o triângulo qualquer com lados \(a\), \(b\) e o ângulo \(\alpha\) entre eles, podemos expressar a altura como:
\[ h = b \cdot \sin(\alpha) \]
Substituindo na fórmula da área:
\[ A = \frac{a \cdot b \cdot \sin(\alpha)}{2} \]
Assim, o seno do ângulo faz o papel da razão entre altura e hipotenusa, permitindo calcular a área mesmo sem conhecer a altura diretamente.
Exemplos resolvidos
Exemplo 1 Básico
Em um triângulo, os lados medem \(a=8\,\text{cm}\) e \(b=6\,\text{cm}\), formando um ângulo de \(60°\). Calcule a área.
Ver solução
\[ A = \frac{a \cdot b \cdot \sin(\alpha)}{2} \]
Substituindo os valores:
\(A = \frac{8 \cdot 6 \cdot \sin(60°)}{2}\)
\(A = \frac{48 \cdot \frac{\sqrt{3}}{2}}{2}\)
\(A = \frac{24\sqrt{3}}{2} = 12\sqrt{3}\,\text{cm}^2 \approx 20{,}8\,\text{cm}^2.\)
Exemplo 2 Intermediário
Um triângulo tem lados \(a=10\,\text{cm}\) e \(b=12\,\text{cm}\), com ângulo de \(45°\) entre eles. Determine a área.
Ver solução
\(A = \dfrac{10 \cdot 12 \cdot \sin(45°)}{2} = \dfrac{120 \cdot \frac{\sqrt{2}}{2}}{2} = 30\sqrt{2}\,\text{cm}^2 \approx 42{,}4\,\text{cm}^2.\)
Exercícios de múltipla escolha (com gabarito)
Tente resolver cada exercício antes de abrir a resposta. Eles variam do nível básico ao avançado.
1) Determine a área de um triângulo onde \(a=7\,\text{cm}\), \(b=9\,\text{cm}\) e \(\alpha=30°\).
Gabarito e solução
\(A = \dfrac{7 \cdot 9 \cdot \sin(30°)}{2} = \dfrac{63 \cdot 0{,}5}{2} = 15{,}75\,\text{cm}^2\Rightarrow\) Letra B.
2) Um triângulo possui lados \(a=8\) e \(b=10\) com ângulo de \(90°\) entre eles. A área é:
Gabarito e solução
\(A = \frac{8\cdot10\cdot\sin(90°)}{2} = \frac{80\cdot1}{2}=40\Rightarrow\) Letra C.
3) Em um triângulo qualquer, \(a=15\), \(b=10\) e \(\alpha=120°\). Calcule a área.
Gabarito e solução
\(A = \dfrac{15 \cdot 10 \cdot \sin(120°)}{2} = 75 \cdot \sin(120°) = 75 \cdot \frac{\sqrt{3}}{2} \approx 64{,}95\Rightarrow\) Letra C.
4) Se um triângulo tem área \(A=24\), lados \(a=8\), \(b=6\), então \(\sin(\alpha)\) é igual a:
Gabarito e solução
\(24=\dfrac{8\cdot6\cdot\sin(\alpha)}{2}\Rightarrow24=24\sin(\alpha)\Rightarrow\sin(\alpha)=1\Rightarrow\) Letra C.
5) (Avançado) Num triângulo, \(a=9\), \(b=12\) e \(A=30\). Determine o valor de \(\sin(\alpha)\).
Gabarito e solução
\(30=\frac{9\cdot12\cdot\sin(\alpha)}{2}\Rightarrow30=54\sin(\alpha)\Rightarrow\sin(\alpha)=0{,}56\Rightarrow\) Letra C.
Dicas finais para lembrar
- A fórmula trigonométrica é útil quando a altura não é conhecida.
- O ângulo usado deve estar entre os dois lados conhecidos.
- O seno é sempre positivo entre \(0°\) e \(180°\), o que garante que a área será positiva.













