Área do triângulo equilátero
Guia prático com fórmula da área, altura \(h=\ell\dfrac{\sqrt{3}}{2}\), perímetro \(P=3\ell\), raio inscrito \(r=\ell\dfrac{\sqrt{3}}{6}\) e circunrádio \(R=\dfrac{\ell}{\sqrt{3}}\). Inclui equivalências com seno e Heron, exemplos resolvidos e exercícios com gabarito.
Reforce com: eBook de Fórmulas • Mapas Mentais • ENEM Matemática • Banco de Questões • 10 eBooks
Fórmulas essenciais
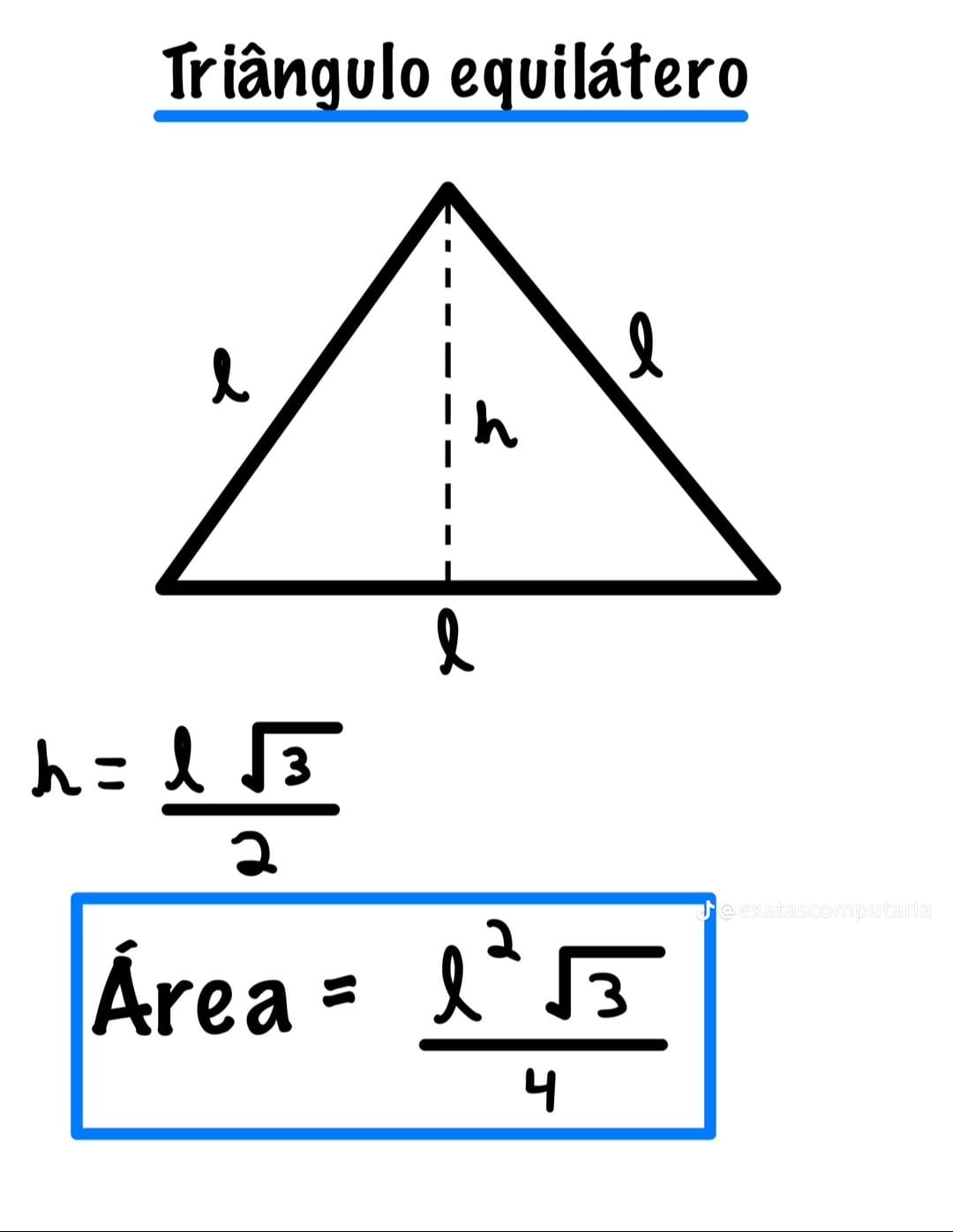
Área e altura
\[ A=\frac{\ell^2\sqrt{3}}{4}\qquad\text{e}\qquad h=\ell\frac{\sqrt{3}}{2} \]
A altura divide o triângulo em dois triângulos \(30^\circ\!-\!60^\circ\!-\!90^\circ\).
Perímetro e raios
\[ P=3\ell,\quad r=\ell\frac{\sqrt{3}}{6},\quad R=\frac{\ell}{\sqrt{3}}\;(=2r) \]
Para área: \(A=r\cdot s\) com \(s=\dfrac{P}{2}=\dfrac{3\ell}{2}\).
Outras expressões equivalentes
\[ A=\frac{1}{2}\ell^2\sin 60^\circ=\frac{1}{2}\ell^2\cdot \frac{\sqrt{3}}{2} =\frac{\ell^2\sqrt{3}}{4} \]
\[ A=\sqrt{s(s-\ell)^3}\quad(s=\tfrac{3\ell}{2}) \quad\text{(Heron)} \]
\[ A=\frac{\ell^3}{4R}\quad\text{com}\; R=\frac{\ell}{\sqrt{3}} \]
📘 Fórmulas sempre à mão
Quer um atalho para a prova? Tenha todas as fórmulas de Geometria (incluindo triângulo equilátero) no eBook Fórmulas Matemática.
Exemplos resolvidos
Exemplo 1 lado conhecido
Para um triângulo equilátero com \(\ell=6\,\text{cm}\), calcule a área.
Ver solução
\(=\dfrac{6^2\sqrt{3}}{4}\)
\(=\dfrac{36\sqrt{3}}{4}\)
\(=9\sqrt{3}\,\text{cm}^2\).
Exemplo 2 perímetro dado
O perímetro é \(P=24\,\text{cm}\). Encontre \(\ell\) e a área.
Ver solução
\(=8\,\text{cm}\).
\(A=\dfrac{8^2\sqrt{3}}{4}\)
\(=\dfrac{64\sqrt{3}}{4}\)
\(=16\sqrt{3}\,\text{cm}^2\).
Exemplo 3 altura conhecida
Sabendo que a altura é \(h=9\,\text{cm}\), determine \(\ell\) e a área.
Ver solução
\(=\dfrac{18}{\sqrt{3}}=6\sqrt{3}\,\text{cm}\).
\(A=\dfrac{(6\sqrt{3})^2\sqrt{3}}{4}\)
\(=\dfrac{108\sqrt{3}}{4}\)
\(=27\sqrt{3}\,\text{cm}^2\).
Exemplo 4 área → lado, r e R
Se \(A=27\sqrt{3}\,\text{cm}^2\), calcule \(\ell\), \(r\) e \(R\).
Ver solução
\(=\dfrac{4\cdot 27\sqrt{3}}{\sqrt{3}}=108\Rightarrow \ell=6\sqrt{3}\).
\(r=\ell\dfrac{\sqrt{3}}{6}=(6\sqrt{3})\dfrac{\sqrt{3}}{6}=3\).
\(R=2r=6\).
Exercícios de múltipla escolha (com gabarito)
Enunciados claros e soluções com os passos um abaixo do outro após cada “=”.
1) Num triângulo equilátero de lado \(\ell=10\,\text{cm}\), a área é:
Gabarito e solução
\(=\dfrac{10^2\sqrt{3}}{4}\)
\(=\dfrac{100\sqrt{3}}{4}\)
\(=25\sqrt{3}\Rightarrow\) Letra B.
2) A altura de um triângulo equilátero é \(h=12\,\text{cm}\). Determine a área.
Gabarito e solução
\(A=\dfrac{(8\sqrt{3})^2\sqrt{3}}{4}\)
\(=\dfrac{192\sqrt{3}}{4}\)
\(=48\sqrt{3}\Rightarrow\) Letra C.
3) O perímetro de um triângulo equilátero é \(30\,\text{cm}\). O raio inscrito \(r\) é:
Gabarito e solução
\(r=\ell\dfrac{\sqrt{3}}{6}=10\dfrac{\sqrt{3}}{6}\)
\(=\dfrac{5\sqrt{3}}{3}\Rightarrow\) Letra B.
4) Se \(A=16\sqrt{3}\,\text{cm}^2\), então o lado \(\ell\) mede:
Gabarito e solução
\(\ell^2=\dfrac{4\cdot 16\sqrt{3}}{\sqrt{3}}=64\)
\(\ell=8\Rightarrow\) Letra C.
5) O circunrádio é \(R=5\,\text{cm}\). O lado \(\ell\) e a área são, respectivamente:
Gabarito e solução
\(A=\dfrac{\ell^2\sqrt{3}}{4}=\dfrac{(5\sqrt{3})^2\sqrt{3}}{4}\)
\(=\dfrac{75\sqrt{3}}{4}\Rightarrow\) Letra A.
6) Para \(\ell=6\,\text{cm}\), o raio inscrito \(r\) é:
Gabarito e solução
\(=\sqrt{3}\Rightarrow\) Letra A.
7) Um triângulo equilátero tem área \(A=9\sqrt{3}\). Seu perímetro é:
Gabarito e solução
\(P=3\ell=18\Rightarrow\) Letra B.
8) Em um triângulo equilátero, a razão \(\dfrac{A}{\ell \cdot h}\) é igual a:
Gabarito e solução
\(\dfrac{A}{\ell h}=\dfrac{\frac{\ell^2\sqrt{3}}{4}}{\ell\cdot \ell\frac{\sqrt{3}}{2}}\)
\(=\dfrac{\frac{\ell^2\sqrt{3}}{4}}{\frac{\ell^2\sqrt{3}}{2}}\)
\(=\dfrac{1}{2}\Rightarrow\) Letra B.
Dicas finais
- Memorize o trio: \(h=\ell\frac{\sqrt{3}}{2}\), \(r=\ell\frac{\sqrt{3}}{6}\), \(R=\dfrac{\ell}{\sqrt{3}}(=2r)\).
- Se o dado for perímetro: \(\ell=\dfrac{P}{3}\) e depois use \(A=\dfrac{\ell^2\sqrt{3}}{4}\).
- Conferir unidades (cm, m) antes de substituir evita erros de escala.













