Área do triângulo com círculo inscrito (A = r·s): fórmula, passo a passo e exercícios
Aprenda como calcular a área do triângulo pela circunferência inscrita usando a relação A = r · s, em que r é o raio do círculo inscrito e s é o semiperímetro \(\big(s=\frac{a+b+c}{2}\big)\). Veja quando usar a fórmula, como encontrar \(r\) e \(s\), a ligação com a Fórmula de Heron e resolva questões no estilo ENEM e vestibulares.
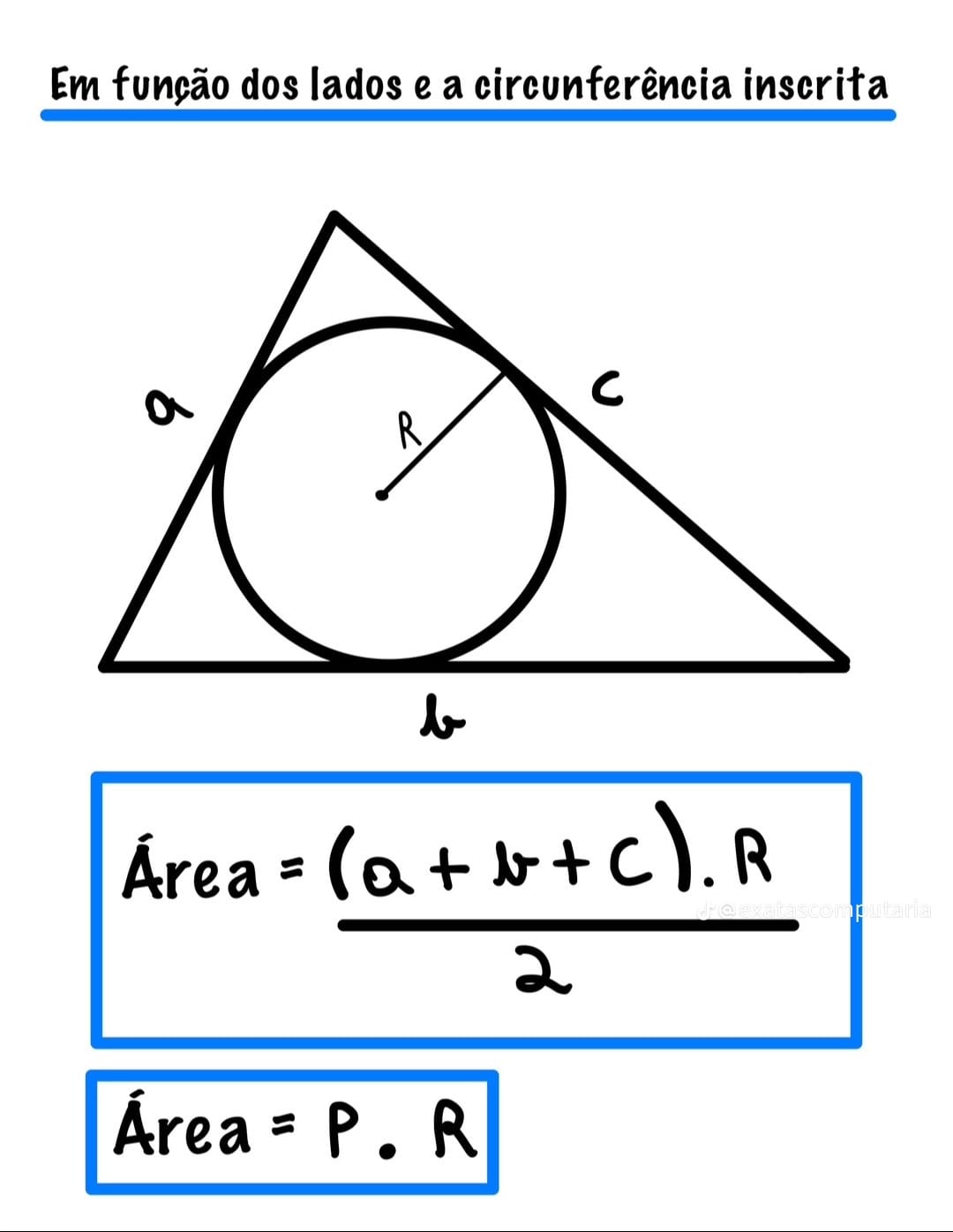
Se você procurou por “área do triângulo com círculo inscrito”, “área com raio inscrito” ou “A = r · s”, aqui vai o resumo rápido: \(A = r \cdot s\). Primeiro calcule \(s=\frac{a+b+c}{2}\); depois multiplique por \(r\). Nos tópicos abaixo você encontra a dedução, exemplos resolvidos e uma lista de exercícios com gabarito.
Dica: revise fórmulas no eBook de Fórmulas, treine no Banco de Questões e veja resumos nos Mapas Mentais.
Fórmulas essenciais
Principal (com semiperímetro)
\[ A=r\cdot s\qquad \text{onde}\quad s=\frac{a+b+c}{2} \]
Alguns livros usam \(p\) para o semiperímetro; a fórmula fica \(A=p\cdot r\).
Isolando \(r\) ou \(s\)
\[ r=\frac{A}{s}\qquad\text{e}\qquad s=\frac{A}{r} \]
Ligação com Heron
\[ A=\sqrt{s(s-a)(s-b)(s-c)}\;\Rightarrow\; r=\frac{A}{s}=\sqrt{\frac{(s-a)(s-b)(s-c)}{s}} \]
Dedução rápida
Ao traçar os três raios até os pontos de tangência, partimos o triângulo em três triângulos retângulos de alturas \(r\). Então:
\[ A=\frac{1}{2}r\,a+\frac{1}{2}r\,b+\frac{1}{2}r\,c =\frac{r(a+b+c)}{2}=r\,s. \]
Aproveite e veja também: eBook de Fórmulas • ENEM Matemática • Mapas Mentais • Banco de Questões • 10 eBooks
📘 Fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática e tenha todas as relações de triângulos (Heron, \(r\), \(R\), seno, cosseno…) organizadas.
Exemplos resolvidos
Exemplo 1 Área a partir de \(r\) e dos lados
No triângulo com \(a=7\), \(b=9\), \(c=10\) e raio do círculo inscrito \(r=3\,\text{cm}\), calcule a área.
Ver solução
\(=\dfrac{7+9+10}{2}\)
\(=\dfrac{26}{2}=13\).
\(A=r\cdot s\)
\(=3\cdot 13\)
\(=39\,\text{cm}^2\).
Exemplo 2 Encontrando \(r\)
Se \(a=6\), \(b=8\), \(c=10\) e \(A=24\,\text{cm}^2\), determine o raio \(r\).
Ver solução
\(=\dfrac{24}{2}=12\).
\(r=\dfrac{A}{s}\)
\(=\dfrac{24}{12}\)
\(=2\,\text{cm}\).
Exemplo 3 Somente com os lados
Para \(a=13\), \(b=14\), \(c=15\), calcule \(r\).
Ver solução
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
\(=\sqrt{21\cdot 8\cdot 7\cdot 6}\)
\(=\sqrt{7056}=84\).
\(r=\dfrac{A}{s}=\dfrac{84}{21}=4\).
Exercícios de múltipla escolha (com gabarito)
Enunciados completos e soluções com os passos um abaixo do outro após cada “=”.
1) Dado \(a=7\), \(b=9\), \(c=10\) e \(r=3\,\text{cm}\), a área do triângulo vale:
Gabarito e solução
\(A=r\cdot s=3\cdot 13\)
\(=39\,\text{cm}^2\Rightarrow\) Letra B.
2) Para \(a=6\), \(b=8\), \(c=10\) e \(A=24\,\text{cm}^2\), o raio inscrito é:
Gabarito e solução
\(r=\dfrac{A}{s}=\dfrac{24}{12}\)
\(=2\,\text{cm}\Rightarrow\) Letra B.
3) Em um triângulo com lados \(13,14,15\), o raio \(r\) do círculo inscrito é:
Gabarito e solução
\(A=\sqrt{21\cdot 8\cdot 7\cdot 6}=84\)
\(r=\dfrac{A}{s}=\dfrac{84}{21}\)
\(=4\Rightarrow\) Letra C.
4) Num triângulo equilátero de lado \(a=12\,\text{cm}\), o raio inscrito é:
Gabarito e solução
\(=\dfrac{12\sqrt{3}}{6}\)
\(=2\sqrt{3}\,\text{cm}\Rightarrow\) Letra A.
5) Sabendo que \(r=5\,\text{cm}\) e \(s=18\,\text{cm}\), a área do triângulo é:
Gabarito e solução
\(=5\cdot 18\)
\(=90\,\text{cm}^2\Rightarrow\) Letra B.
6) Para um triângulo isósceles com lados \(5,5,6\), o raio inscrito \(r\) vale:
Gabarito e solução
\(A=\sqrt{8(8-5)(8-5)(8-6)}\)
\(=\sqrt{8\cdot 3\cdot 3\cdot 2}=\sqrt{144}=12\)
\(r=\dfrac{A}{s}=\dfrac{12}{8}=1{,}5\,\text{cm}\Rightarrow\) Letra B.
7) Se \(A=25\,\text{cm}^2\) e \(r=2{,}5\,\text{cm}\), o semiperímetro \(s\) é:
Gabarito e solução
\(=\dfrac{25}{2{,}5}\)
\(=10\,\text{cm}\Rightarrow\) Letra B.
8) Num triângulo retângulo com catetos \(9\) e \(12\), o raio \(r\) do círculo inscrito é:
Gabarito e solução
\(c=\sqrt{9^2+12^2}=15\)
\(s=\dfrac{9+12+15}{2}=18\)
\(r=\dfrac{A}{s}=\dfrac{54}{18}=3\Rightarrow\) Letra C.
Dicas finais
- Sem \(r\)? Use Heron para achar \(A\) e então \(r=\dfrac{A}{s}\).
- Triângulos especiais: equilátero \(r=\dfrac{a\sqrt3}{6}\); retângulo \(r=\dfrac{a+b-c}{2}\).
- Verifique as unidades (cm, m) antes de substituir.













