Área do Triângulo Retângulo: fórmula \(A=\dfrac{b\cdot c}{2}\), exemplos e exercícios
Tudo o que você precisa para dominar a área do triângulo retângulo — teoria, passo a passo e lista de questões com gabarito.
Definição e fórmula
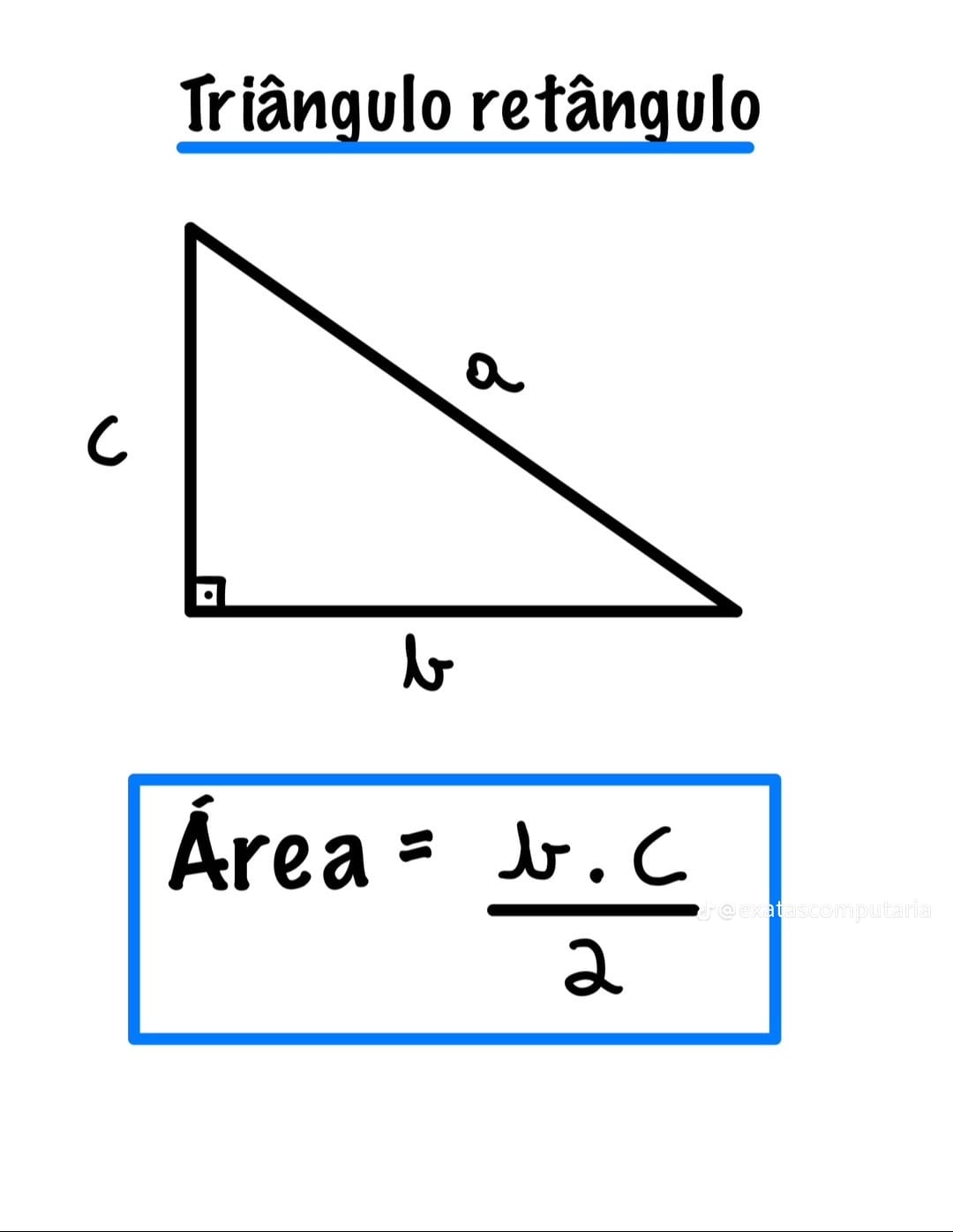
O triângulo retângulo possui um ângulo de \(90^\circ\). Os lados que formam o ângulo reto são os catetos e o lado oposto ao ângulo reto é a hipotenusa.
Fórmula principal da área
\[ A=\frac{\text{cateto}_1\cdot \text{cateto}_2}{2}=\frac{b\cdot c}{2} \]
É a metade do retângulo formado pelos catetos.
Outras formas úteis
\[ A=\frac{\text{hipotenusa}\cdot \text{altura à hipotenusa}}{2}=\frac{a\cdot h_a}{2} \]
\[ A=\frac{1}{2}\,b\,c\,\sin(90^\circ)=\frac{b\,c}{2} \]
Se faltar um cateto, use Pitágoras: \(a^2=b^2+c^2\).
Veja também: Mapas Mentais • ENEM Matemática • Banco de Questões
📘 Fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática e acelere suas revisões de Geometria Plana e Trigonometria.
Exemplos resolvidos
Exemplo 1 Básico
Calcule a área do triângulo retângulo com catetos \(b=6\,\text{cm}\) e \(c=8\,\text{cm}\).
Ver solução
\[ A=\frac{b\cdot c}{2} \]
\(A=\frac{6\cdot 8}{2}\)
\(A=\frac{48}{2}\)
\(A=24\,\text{cm}^2\).
Exemplo 2 Com Pitágoras
Dado \(a=13\,\text{cm}\) (hipotenusa) e um cateto \(b=5\,\text{cm}\), determine a área.
Ver solução
Primeiro o outro cateto: \(c=\sqrt{a^2-b^2}\).
\(c=\sqrt{13^2-5^2}\)
\(c=\sqrt{169-25}\)
\(c=\sqrt{144}=12\,\text{cm}\).
Agora a área:
\(A=\frac{b\cdot c}{2}\)
\(A=\frac{5\cdot 12}{2}\)
\(A=\frac{60}{2}=30\,\text{cm}^2\).
Exemplo 3 Aplicado
Uma rampa forma um triângulo retângulo com base \(3{,}6\,\text{m}\) e altura \(1{,}2\,\text{m}\). Quantos metros quadrados de material são necessários para cobrir a superfície triangular?
Ver solução
\(A=\dfrac{3{,}6\cdot 1{,}2}{2}=2{,}16\,\text{m}^2\).
Exercícios de múltipla escolha (com gabarito)
Resolva e depois abra o gabarito. Dificuldade crescente.
1) Em um triângulo retângulo, \(b=7\,\text{cm}\) e \(c=6\,\text{cm}\). A área é:
Gabarito e solução
\(A=\dfrac{7\cdot 6}{2}=21\Rightarrow\) Letra C.
2) Num triângulo retângulo, \(a=15\,\text{cm}\) e \(b=9\,\text{cm}\). A área é:
Gabarito e solução
Cateto \(c=\sqrt{15^2-9^2}=\sqrt{225-81}=\sqrt{144}=12.\)
\(A=\dfrac{9\cdot 12}{2}=54\Rightarrow\) Letra C.
3) A altura à hipotenusa vale \(h_a=4\,\text{cm}\) e a hipotenusa \(a=10\,\text{cm}\). A área é:
Gabarito e solução
\(A=\dfrac{a\cdot h_a}{2}=\dfrac{10\cdot 4}{2}=20\Rightarrow\) Letra C.
4) Um triângulo retângulo tem área \(A=30\,\text{cm}^2\) e um cateto \(b=5\,\text{cm}\). O outro cateto vale:
Gabarito e solução
\(30=\dfrac{5\cdot c}{2}\Rightarrow 60=5c\Rightarrow c=12\Rightarrow\) Letra C.
5) Um terreno triangular retângulo tem base \(9\,\text{m}\) e altura \(4\,\text{m}\). Cada lata de tinta rende \(6\,\text{m}^2\). Quantas latas são necessárias para pintá-lo?
Gabarito e solução
Área: \(A=\dfrac{9\cdot 4}{2}=18\,\text{m}^2\). Latas: \(18/6=3\Rightarrow\) Letra B.
6) Para um triângulo retângulo \(8\!-\!15\!-\!17\), a área é:
Gabarito e solução
\(A=\dfrac{8\cdot 15}{2}=60\Rightarrow\) Letra C.
7) Num triângulo retângulo, a soma dos catetos é \(b+c=20\) e a área é \(A=96\). Se \(b>c\), o valor do maior cateto é:
Gabarito e solução
\(\dfrac{b c}{2}=96\Rightarrow bc=192\) e \(b+c=20\).
Equação: \(t^2-20t+192=0\Rightarrow (t-12)(t-16)=0\Rightarrow t\in\{12,16\}\).
Logo os catetos são \(12\) e \(16\) e o maior é 16 → Letra C.
8) (Avançado) Um triângulo retângulo tem hipotenusa \(a=10\) e área \(A=20\). O valor da altura à hipotenusa é:
Gabarito e solução
\(A=\dfrac{a\cdot h_a}{2}\Rightarrow 20=\dfrac{10\cdot h_a}{2}\Rightarrow 20=5h_a\Rightarrow h_a=4\Rightarrow\) Letra B.
Dicas finais
- Se conhecer a hipotenusa e um cateto, use Pitágoras para achar o outro cateto e aplicar \(A=\dfrac{bc}{2}\).
- Em problemas práticos, confira unidades (cm, m) e arredondamentos.
- Para triângulo retângulo isósceles (\(b=c\)), \(A=\dfrac{b^2}{2}\).













