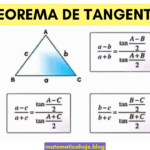
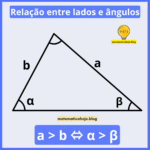
Áreas de Figuras Planas

Neste guia reunimos as fórmulas de área de quadrado, retângulo, paralelogramo, triângulo, trapézio, losango e polígonos regulares, com imagens (50%), exemplos resolvidos e links para estudos detalhados no Matemática Hoje.

Estude cada tema a fundo: Área do Quadrado · Áreas do Retângulo · Área do Paralelogramo · Área de Triângulo · Área do Trapézio · Área do Losango · Área de Polígonos Regulares.

1) Quadrado

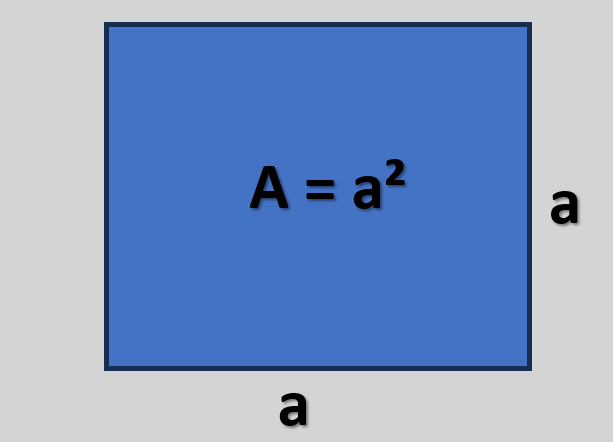
Quadrado de lado a e diagonal d — Quadrado: lado \(a\), diagonal \(d\).

\[ \boxed{A=a^2} \]

\[ \boxed{A=\frac{d^2}{2}} \quad(\text{usando a diagonal}) \]

Exemplo 1

Um piso quadrado tem lado \(a=6\,\text{cm}\). Calcule a área.

Ver solução

\[ \begin{aligned} A&=a^2\\ &=6^2\\ &=\boxed{36\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (pela diagonal)

Um quadro quadrado possui diagonal \(d=10\,\text{cm}\). Encontre a área.

Ver solução

\[ \begin{aligned} A&=\frac{d^2}{2}\\ &=\frac{10^2}{2}\\ &=\boxed{50\ \text{cm}^2} \end{aligned} \]

Veja mais: guia completo de Área do Quadrado.

2) Retângulo

Retângulo com base b e altura h — Retângulo: base \(b\) e altura \(h\).

\[ \boxed{A=b\cdot h} \]

Exemplo 1

Uma placa retangular tem \(b=8\,\text{cm}\) e \(h=5\,\text{cm}\). Calcule a área.

Ver solução

\[ \begin{aligned} A&=b\cdot h\\ &=8\cdot 5\\ &=\boxed{40\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (com perímetro)

Um retângulo tem base \(b=12\,\text{cm}\) e perímetro \(P=40\,\text{cm}\). Encontre a área.

Ver solução

\[ \begin{aligned} P&=2(b+h)\\ 40&=2(12+h)\\ 20&=12+h\\ h&=8\\[6pt] A&=b\cdot h\\ &=12\cdot 8\\ &=\boxed{96\ \text{cm}^2} \end{aligned} \]

Aprofunde: tudo sobre Áreas do Retângulo.

3) Paralelogramo

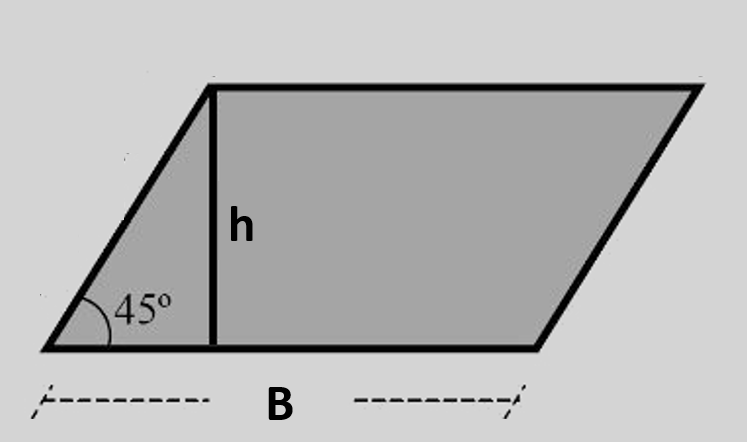
Paralelogramo com base b e altura h ou lados a e b com ângulo entre eles — Paralelogramo: \(A=b\cdot h\) ou \(A=ab\sin\theta\).

\[ \boxed{A=b\cdot h} \]

\[ \boxed{A=a\,b\,\sin\theta} \quad(\text{ângulo }\theta\text{ entre os lados }a\text{ e }b) \]

Exemplo 1

Um paralelogramo tem base \(b=9\,\text{cm}\) e altura \(h=4\,\text{cm}\). Calcule a área.

Ver solução

\[ \begin{aligned} A&=b\cdot h\\ &=9\cdot 4\\ &=\boxed{36\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (com ângulo)

Num paralelogramo, \(a=10\,\text{cm}\), \(b=7\,\text{cm}\) e \(\theta=60^\circ\). Encontre a área.

Ver solução

\[ \begin{aligned} A&=a\,b\,\sin\theta\\ &=10\cdot 7\cdot \sin 60^\circ\\ &=70\cdot \frac{\sqrt{3}}{2}\\ &\approx 70\cdot 0{,}866025\\ &\approx \boxed{60{,}62\ \text{cm}^2} \end{aligned} \]

Leia: Área do Paralelogramo (propriedades, casos com vetores e mais).

4) Triângulo

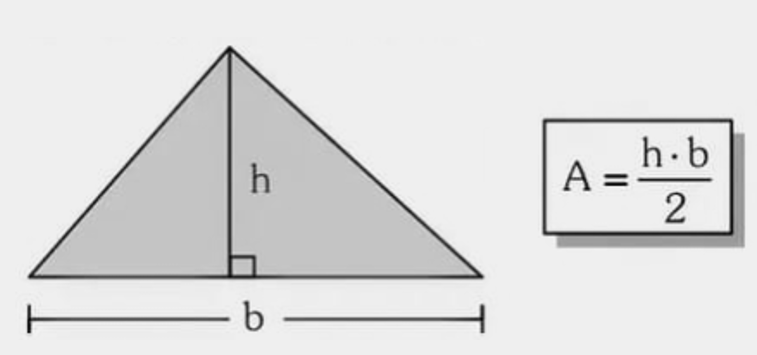
Triângulo com base b e altura h — Triângulo: área por base-altura ou por Heron (lados).

\[ \boxed{A=\frac{b\cdot h}{2}} \]

\[ \text{(Heron)}\quad \boxed{A=\sqrt{s(s-a)(s-b)(s-c)}}\ ,\ s=\frac{a+b+c}{2} \]

Exemplo 1 (base-altura)

Num triângulo, \(b=10\,\text{cm}\) e \(h=6\,\text{cm}\). Calcule a área.

Ver solução

\[ \begin{aligned} A&=\frac{b\cdot h}{2}\\ &=\frac{10\cdot 6}{2}\\ &=\boxed{30\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (Heron)

Para lados \(a=7\), \(b=8\), \(c=9\) (cm), calcule a área pelo método de Heron.

Ver solução

\[ \begin{aligned} s&=\frac{a+b+c}{2}\\ &=\frac{7+8+9}{2}\\ &=12\\[6pt] A&=\sqrt{s(s-a)(s-b)(s-c)}\\ &=\sqrt{12\cdot 5\cdot 4\cdot 3}\\ &=\sqrt{720}\\ &\approx \boxed{26{,}83\ \text{cm}^2} \end{aligned} \]

Veja: guia de Área de Triângulo (casos especiais, altura em equilátero, trigonometria, etc.).

5) Trapézio

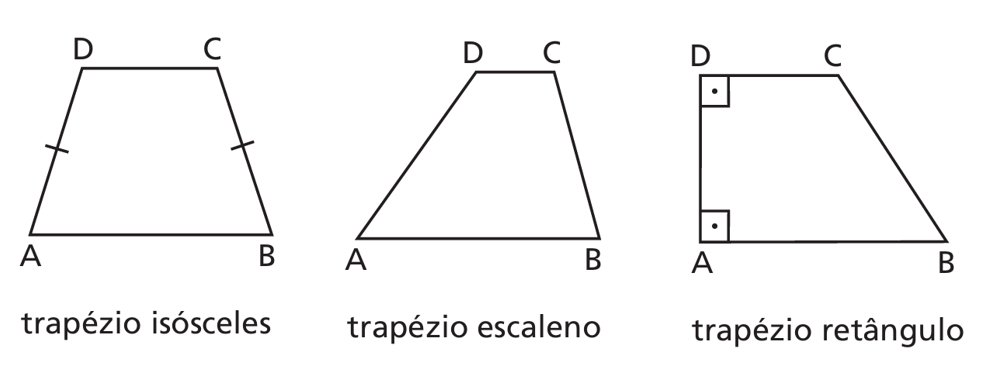
Trapézio com bases B e b e altura h — Trapézio: bases \(B\) e \(b\) (\(B>b\)), altura \(h\).

\[ \boxed{A=\frac{(B+b)\cdot h}{2}} \]

Exemplo 1

Um trapézio tem \(B=12\), \(b=8\), \(h=5\) (cm). Calcule a área.

Ver solução

\[ \begin{aligned} A&=\frac{(B+b)\cdot h}{2}\\ &=\frac{(12+8)\cdot 5}{2}\\ &=\frac{20\cdot 5}{2}\\ &=\boxed{50\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (isósceles, altura via lado)

Trapézio isósceles com \(B=14\), \(b=6\) e lado \(l=5\) (cm). Encontre \(A\).

Ver solução

\[ \begin{aligned} x&=\frac{B-b}{2}=\frac{14-6}{2}=4\\ h&=\sqrt{l^2-x^2}=\sqrt{5^2-4^2}=\sqrt{25-16}=3\\[6pt] A&=\frac{(B+b)\cdot h}{2}\\ &=\frac{(14+6)\cdot 3}{2}\\ &=\frac{20\cdot 3}{2}\\ &=\boxed{30\ \text{cm}^2} \end{aligned} \]

Aprenda mais: Área do Trapézio (retângulo, isósceles, escaleno e problemas clássicos).

6) Losango

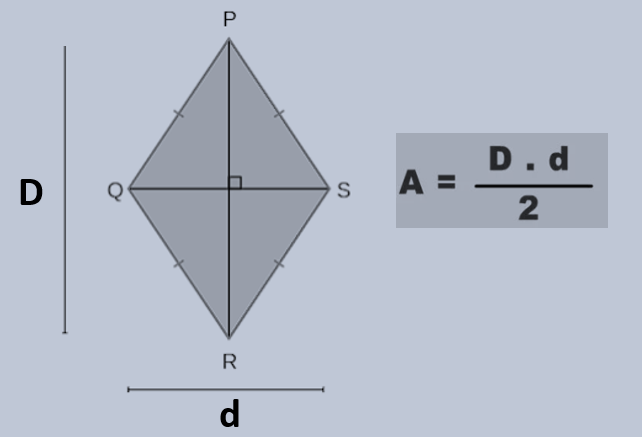
Losango com diagonais D e d — Losango: diagonais \(D\) e \(d\); também \(A=a^2\sin\theta\).

\[ \boxed{A=\frac{D\cdot d}{2}} \]

\[ \boxed{A=a^2\sin\theta} \quad(\text{lado }a,\ \text{ângulo interno }\theta) \]

Exemplo 1 (diagonais)

Num losango, \(D=10\,\text{cm}\) e \(d=8\,\text{cm}\). Calcule \(A\).

Ver solução

\[ \begin{aligned} A&=\frac{D\cdot d}{2}\\ &=\frac{10\cdot 8}{2}\\ &=\boxed{40\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (lado e ângulo)

Losango de lado \(a=6\,\text{cm}\) e ângulo \(\theta=30^\circ\). Calcule a área.

Ver solução

\[ \begin{aligned} A&=a^2\sin\theta\\ &=6^2\cdot \sin 30^\circ\\ &=36\cdot 0{,}5\\ &=\boxed{18\ \text{cm}^2} \end{aligned} \]

Detalhes: Área do Losango (diagonais, altura, perímetro e aplicações).

7) Polígonos Regulares

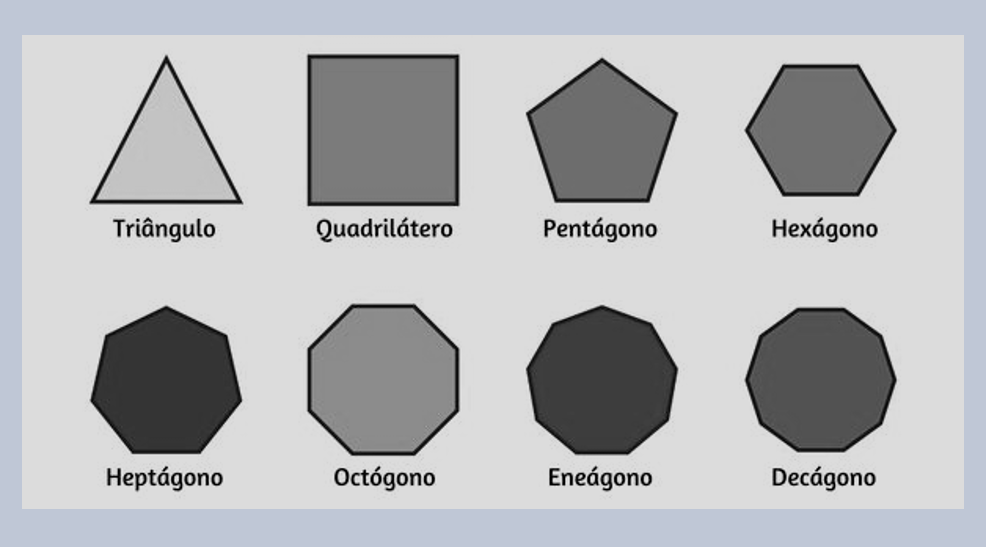
Polígono regular com lado s, apótema ap e n lados — Polígono regular: lado \(s\), apótema \(ap\), \(n\) lados.

\[ \boxed{A=\frac{P\cdot ap}{2}} \quad(\text{com }P=n\cdot s) \]

\[ \boxed{A=\frac{n\,s^2}{4\tan\!\left(\frac{\pi}{n}\right)}} \]

Exemplo 1 (hexágono regular)

Hexágono regular com lado \(s=4\,\text{cm}\). Encontre a área.

Ver solução

\[ \begin{aligned} n&=6,\quad P=n s=6\cdot 4=24\\ ap&=\frac{s}{2\tan(\pi/n)}=\frac{4}{2\tan(\pi/6)}=\frac{4}{2\cdot 0{,}57735}=3{,}4641\\[6pt] A&=\frac{P\cdot ap}{2}\\ &=\frac{24\cdot 3{,}4641}{2}\\ &\approx \boxed{41{,}57\ \text{cm}^2} \end{aligned} \]

Exemplo 2 (pentágono regular)

Pentágono regular com lado \(s=10\,\text{cm}\). Calcule a área.

Ver solução

\[ \begin{aligned} n&=5\\ A&=\frac{n s^2}{4\tan(\pi/n)}\\ &=\frac{5\cdot 10^2}{4\tan(\pi/5)}\\ &=\frac{500}{4\cdot \tan 36^\circ}\\ &=\frac{500}{4\cdot 0{,}726543}\\ &=\frac{500}{2{,}906172}\\ &\approx \boxed{171{,}01\ \text{cm}^2} \end{aligned} \]

Aprenda o método geral: Área de Polígonos Regulares (apotema, perímetro e casos clássicos).