Do Conceito de Integral ao Teorema Fundamental do Cálculo
Após compreendermos a definição de integral como limite de somas de Riemann, nosso próximo objetivo é encontrar maneiras práticas de calcular integrais, sem precisar recorrer à definição formal em cada situação. Para isso, partimos das propriedades básicas da integral definida e caminhamos até o Teorema Fundamental do Cálculo, que conecta integral e derivada.
1. O Caminho para Calcular Integrais
A definição de integral permite que aproximemos a área sob uma curva por retângulos. No entanto, esse método é trabalhoso e pouco prático. O que buscamos é uma técnica que utilize antiderivadas: encontrar uma função cuja derivada seja a função que desejamos integrar. Isso é possível graças ao Teorema Fundamental do Cálculo, que será introduzido a seguir.
2. Propriedades Básicas da Integral Definida
Antes de chegarmos ao teorema, precisamos entender algumas propriedades fundamentais da integral definida:
- Função constante: \(\int_a^b c \, dx = c (b – a)\).
- Linearidade: \[ \int_a^b [f(x) + g(x)] \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx, \] \[ \int_a^b k f(x) \, dx = k \int_a^b f(x) \, dx, \] onde \(k\) é uma constante real.
- Comparação: Se \(f(x) \ge 0\) em \([a, b]\), então \(\int_a^b f(x) dx \ge 0\).
- Limites de funções: Se \(m \le f(x) \le M\) em \([a, b]\), então: \[ m(b-a) \le \int_a^b f(x) \, dx \le M(b-a). \]
- Propriedade aditiva: \[ \int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx, \] para qualquer \(c \in [a, b]\).
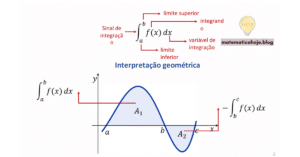
3. A Interpretação Geométrica
A integral definida continua sendo interpretada como uma área. Se \(f(x) \ge 0\), ela representa a área sob o gráfico da função entre \(x = a\) e \(x = b\). Se \(f(x)\) assume valores negativos, a área abaixo do eixo \(x\) conta como negativa, resultando na chamada área líquida.
4. Um Exemplo Intuitivo: Distância e Velocidade
Imagine um carro viajando de Campinas a São Paulo, um trajeto de aproximadamente 100 km. Se a velocidade fosse constante, poderíamos simplesmente multiplicar velocidade e tempo para obter a distância. No entanto, a velocidade varia: o carro acelera, reduz em pedágios e, às vezes, para.
A distância total percorrida é dada pela área sob o gráfico da velocidade em função do tempo:
\[ D = \int_0^T v(t) \, dt, \] onde \(v(t)\) é a velocidade e \(T\) o tempo total da viagem.Se quisermos saber a distância percorrida até um instante \(t_0\), definimos:
\[ D(t_0) = \int_0^{t_0} v(t) \, dt. \] A função \(D(t)\) cresce à medida que o tempo avança e sua derivada é a própria velocidade: \[ D'(t) = v(t). \] Isso mostra a conexão direta entre derivada e integral.5. Teorema Fundamental do Cálculo
O Teorema Fundamental do Cálculo formaliza essa ideia. Ele afirma que se \(f\) é contínua em \([a, b]\) e definimos:
\[ F(x) = \int_a^x f(t) \, dt, \] então \(F'(x) = f(x)\).Além disso, para qualquer antiderivada \(F(x)\) de \(f(x)\), temos: \[ \int_a^b f(x) \, dx = F(b) – F(a). \] Esse resultado nos permite calcular integrais apenas encontrando antiderivadas, sem recorrer à definição de somas de Riemann.
6. Exemplos
Exemplo 1:
Calcule \(\int_0^2 x \, dx\).
Solução:
\[ \int_0^2 x \, dx = \left[ \frac{x^2}{2} \right]_0^2 = \frac{4}{2} – 0 = 2. \]Exemplo 2:
Se \(v(t) = 60 + 10t\) (em km/h), a distância percorrida nos primeiros 2 h é:
\[ D = \int_0^2 (60 + 10t) \, dt = \left[ 60t + 5t^2 \right]_0^2 = 120 + 20 = 140 \, \text{km}. \]7. Conclusão
Com o Teorema Fundamental do Cálculo, a integração deixa de ser apenas um conceito geométrico e torna-se uma ferramenta prática, diretamente ligada à derivação. Agora, o desafio é aprender técnicas para encontrar antiderivadas e resolver integrais mais complexas.
📚 Melhores Livros de Cálculo 1

Cálculo: Volume 1
Um dos livros mais utilizados em cursos de graduação, ideal para quem quer uma abordagem completa, com exercícios desafiadores e explicações claras.
🔗 Comprar na Amazon
Cálculo: Volume 1
Este livro se destaca por exemplos visuais e didáticos, facilitando a compreensão dos conceitos fundamentais do Cálculo Diferencial e Integral.
🔗 Comprar na Amazon
Pré-Cálculo – Uma Preparação para o Cálculo
Ideal para quem precisa reforçar a base matemática antes de iniciar o estudo do Cálculo, com revisões de álgebra e funções.
🔗 Comprar na Amazon
Cálculo com Geometria Analítica: Volume 1
Combina teoria do cálculo com a geometria analítica, ajudando na visualização gráfica e no entendimento geométrico das funções.
🔗 Comprar na Amazon
Um Curso de Cálculo – Vol. 1
Um livro clássico, com abordagem sólida e uma ampla variedade de exercícios, perfeito para estudantes de engenharia e ciências exatas.
🔗 Comprar na Amazon🟣 Curso Completo de Cálculo 1
Aprenda Cálculo 1 com conteúdos completos em artigos didáticos e uma playlist de vídeos com explicações passo a passo. Escolha a forma ideal para estudar:
📖 Curso Completo de Cálculo 1 (Artigos) ▶ Curso Completo de Cálculo 1 (Vídeos)🚀 Domine os conceitos fundamentais e esteja pronto para qualquer desafio de Cálculo 1!