Circunferência e Círculo

Estudamos, separadamente, círculo, setor, segmento e coroa (anel) circular, sempre com a imagem do tipo de figura (em 50% da largura), fórmulas essenciais e exercícios resolvidos passo a passo.

Leituras relacionadas: comprimento da circunferência, área do círculo, área do setor e raio, diâmetro e cordas.

1) Círculo

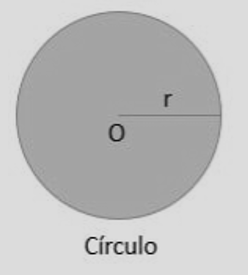
Círculo de raio r e centro O — Região interna da circunferência. Raio \(r\), centro \(O\).

Definição. Círculo é a região formada por todos os pontos a distância menor ou igual a \(r\) do centro \(O\).

\[ \textbf{Área:}\quad \boxed{A=\pi r^2} \]

\[ \textbf{Perímetro (circunferência):}\quad \boxed{C=2\pi r} \]

Exemplo resolvido (círculo)

Um jardim circular tem raio \(r=7\,\text{m}\). Calcule a área e o comprimento da borda.

Ver solução passo a passo

\[ \begin{aligned} A&=\pi r^2\\ &=\pi\cdot 7^2\\ &=49\pi\ \text{m}^2\\[6pt] C&=2\pi r\\ &=2\pi\cdot 7\\ &=14\pi\ \text{m} \end{aligned} \]

Exercícios resolvidos — Círculo

(C1) Um prato circular tem raio \(r=9\,\text{cm}\). Encontre \(A\) e \(C\).

Mostrar solução

\[ \begin{aligned} A&=\pi r^2\\ &=\pi\cdot 9^2\\ &=81\pi\ \text{cm}^2\\[6pt] C&=2\pi r\\ &=2\pi\cdot 9\\ &=\boxed{18\pi\ \text{cm}} \end{aligned} \]

(C2) Uma fonte circular tem diâmetro \(d=20\,\text{m}\). Determine \(A\) e \(C\).

Mostrar solução

\[ \begin{aligned} r&=\frac{d}{2}\\ &=\frac{20}{2}\\ &=10\ \text{m}\\[6pt] A&=\pi r^2\\ &=\pi\cdot 10^2\\ &=\boxed{100\pi\ \text{m}^2}\\[6pt] C&=2\pi r\\ &=2\pi\cdot 10\\ &=\boxed{20\pi\ \text{m}} \end{aligned} \]

(C3) Considere que o lago pode ser modelado como um círculo. Mediu-se a borda e obteve-se \(C=31{,}4\,\text{m}\). Encontre \(r\) e \(A\).

Mostrar solução

\[ \begin{aligned} r&=\frac{C}{2\pi}\\ &=\frac{31{,}4}{2\pi}\\ &\approx 5{,}0\ \text{m}\\[6pt] A&=\pi r^2\\ &=\pi\cdot 5^2\\ &\approx \boxed{78{,}54\ \text{m}^2} \end{aligned} \]

2) Setor circular

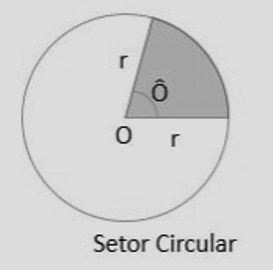
Setor circular com ângulo central alfa e raio r — Parte do círculo delimitada por dois raios e um arco; ângulo central \(\alpha\).

Definição. O setor é a “fatia” do círculo formada por dois raios e o arco entre eles.

\[ \textbf{Arco (graus):}\quad \boxed{L=\tfrac{\alpha}{360^\circ}\,2\pi r} \qquad \textbf{Arco (rad):}\quad \boxed{L=r\theta} \]

\[ \textbf{Área:}\quad \boxed{A_{\text{set}}=\tfrac{\alpha}{360^\circ}\,\pi r^2=\tfrac{\theta}{2}\,r^2} \]

Exemplo resolvido (setor)

Num mostrador, o ponteiro percorre um setor com \(\alpha=75^\circ\) em um círculo de raio \(r=12\,\text{cm}\). Encontre o comprimento do arco e a área.

Ver solução passo a passo

\[ \begin{aligned} L&=\frac{75^\circ}{360^\circ}2\pi\cdot 12\\ &=\frac{5}{24}\cdot 24\pi\\ &=\boxed{5\pi\ \text{cm}}\\[6pt] A_{\text{set}}&=\frac{75^\circ}{360^\circ}\pi\cdot 12^2\\ &=\frac{5}{24}\cdot 144\pi\\ &=\boxed{30\pi\ \text{cm}^2} \end{aligned} \]

Exercícios resolvidos — Setor

(S1) \(r=10\,\text{cm}\) e \(\alpha=60^\circ\). Calcule \(L\) e \(A_{\text{set}}\).

Mostrar solução

\[ \begin{aligned} L&=\frac{60^\circ}{360^\circ}\,2\pi\cdot 10\\ &=\frac{1}{6}\cdot 20\pi\\ &=\boxed{\tfrac{10\pi}{3}\ \text{cm}}\\[6pt] A_{\text{set}}&=\frac{60^\circ}{360^\circ}\,\pi\cdot 10^2\\ &=\frac{1}{6}\cdot 100\pi\\ &=\boxed{\tfrac{50\pi}{3}\ \text{cm}^2} \end{aligned} \]

(S2) \(r=8\,\text{cm}\) e \(\alpha=135^\circ\). Calcule \(L\) e \(A_{\text{set}}\).

Mostrar solução

\[ \begin{aligned} L&=\frac{135^\circ}{360^\circ}\,2\pi\cdot 8\\ &=\frac{3}{8}\cdot 16\pi\\ &=\boxed{6\pi\ \text{cm}}\\[6pt] A_{\text{set}}&=\frac{135^\circ}{360^\circ}\,\pi\cdot 8^2\\ &=\frac{3}{8}\cdot 64\pi\\ &=\boxed{24\pi\ \text{cm}^2} \end{aligned} \]

(S3) \(r=12\,\text{cm}\) e \(\theta=1{,}2\,\text{rad}\). Calcule \(L\) e \(A_{\text{set}}\).

Mostrar solução

\[ \begin{aligned} L&=r\theta\\ &=12\cdot 1{,}2\\ &=\boxed{14{,}4\ \text{cm}}\\[6pt] A_{\text{set}}&=\frac{\theta}{2}r^2\\ &=\frac{1{,}2}{2}\cdot 12^2\\ &=0{,}6\cdot 144\\ &=\boxed{86{,}4\ \text{cm}^2} \end{aligned} \]

3) Segmento circular

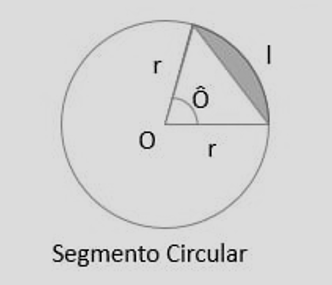
Segmento circular entre uma corda e o arco correspondente — Região entre uma corda e o arco correspondente.

Definição. Segmento circular é a área limitada por uma corda e o arco por ela subtendido.

\[ \textbf{Área (por ângulo em radianos):}\quad \boxed{A_{\text{seg}}=\frac{r^2}{2}\,\bigl(\theta-\sin\theta\bigr)} \]

(\(\theta\) é o ângulo central em radianos.)

Exemplo resolvido (segmento)

Em uma tampa de raio \(r=12\,\text{cm}\) forma-se um segmento com \(\theta=1{,}2\,\text{rad}\). Encontre a área.

Ver solução passo a passo

\[ \begin{aligned} A_{\text{seg}}&=\frac{r^2}{2}(\theta-\sin\theta)\\ &=\frac{12^2}{2}\,\bigl(1{,}2-\sin 1{,}2\bigr)\\ &=72\,\bigl(1{,}2-0{,}932039\bigr)\\ &=72\cdot 0{,}267961\\ &=\boxed{19{,}30\ \text{cm}^2} \end{aligned} \]

Exercícios resolvidos — Segmento

(G1) \(r=10\,\text{cm}\) e \(\theta=1{,}0\,\text{rad}\). Calcule \(A_{\text{seg}}\).

Mostrar solução

\[ \begin{aligned} A_{\text{seg}}&=\frac{r^2}{2}(\theta-\sin\theta)\\ &=\frac{10^2}{2}\,(1-\sin 1)\\ &=50\,(1-0{,}84147098)\\ &=50\cdot 0{,}15852902\\ &=\boxed{7{,}93\ \text{cm}^2} \end{aligned} \]

(G2) \(r=15\,\text{cm}\) e \(\theta=2{,}0\,\text{rad}\). Calcule \(A_{\text{seg}}\).

Mostrar solução

\[ \begin{aligned} A_{\text{seg}}&=\frac{r^2}{2}(\theta-\sin\theta)\\ &=\frac{15^2}{2}\,(2- \sin 2)\\ &=112{,}5\,(2-0{,}909297)\\ &=112{,}5\cdot 1{,}090703\\ &=\boxed{122{,}70\ \text{cm}^2} \end{aligned} \]

(G3) \(r=8\,\text{cm}\) e \(\theta=0{,}7\,\text{rad}\). Calcule \(A_{\text{seg}}\).

Mostrar solução

\[ \begin{aligned} A_{\text{seg}}&=\frac{r^2}{2}(\theta-\sin\theta)\\ &=\frac{8^2}{2}\,(0{,}7-\sin 0{,}7)\\ &=32\,(0{,}7-0{,}645335)\\ &=32\cdot 0{,}054665\\ &=\boxed{1{,}75\ \text{cm}^2} \end{aligned} \]

4) Coroa (anel) circular

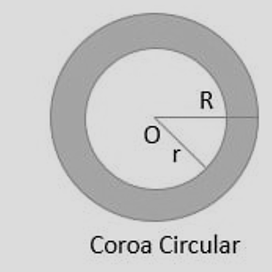
Coroa circular com raios R e r — Região entre duas circunferências concêntricas de raios \(R\) e \(r\) \((R>r)\).

Definição. A coroa é a “faixa” entre dois círculos concêntricos.

\[ \textbf{Área:}\quad \boxed{A_{\text{coroa}}=\pi\,(R^2-r^2)} \]

Exemplo resolvido (coroa)

Um anel decorativo possui raios \(R=18\,\text{cm}\) e \(r=10\,\text{cm}\). Calcule a área.

Ver solução passo a passo

\[ \begin{aligned} A_{\text{coroa}}&=\pi(R^2-r^2)\\ &=\pi(18^2-10^2)\\ &=\pi(324-100)\\ &=\pi\cdot 224\\ &=\boxed{224\pi\ \text{cm}^2\ (\approx 703{,}72)} \end{aligned} \]

Exercícios resolvidos — Coroa

(A1) \(R=10\,\text{cm}\) e \(r=6\,\text{cm}\). Calcule a área.

Mostrar solução

\[ \begin{aligned} A_{\text{coroa}}&=\pi(R^2-r^2)\\ &=\pi(10^2-6^2)\\ &=\pi(100-36)\\ &=\boxed{64\pi\ \text{cm}^2\ (\approx 201{,}06)} \end{aligned} \]

(A2) \(R=25\,\text{cm}\) e \(r=20\,\text{cm}\). Determine a área.

Mostrar solução

\[ \begin{aligned} A_{\text{coroa}}&=\pi(R^2-r^2)\\ &=\pi(25^2-20^2)\\ &=\pi(625-400)\\ &=\boxed{225\pi\ \text{cm}^2\ (\approx 706{,}86)} \end{aligned} \]

(A3) A área do anel é \(200\pi\ \text{cm}^2\) e \(R=15\,\text{cm}\). Encontre \(r\).

Mostrar solução

\[ \begin{aligned} A_{\text{coroa}}&=\pi(R^2-r^2)\\ 200\pi&=\pi(15^2-r^2)\\ 200&=225-r^2\\ r^2&=25\\ r&=\boxed{5\ \text{cm}} \end{aligned} \]