Pratique e domine análise combinatória com este exercícios resolvidos passo a passo! Explore conceitos fundamentais da matemática, como permutação, combinação e arranjo, de forma clara e objetiva. Baixe o PDF com exercícios de análise combinatória e tenha uma ferramenta completa para estudar offline e se preparar para provas e concursos.
Questão de Analise Combinatória – Combinação
Quantos produtos podemos obter se tomarmos 3 fatores distintos escolhidos entre 2, 3, 5, 7 e 11?
Ver Solução
1 – Análise Combinatória – Combinação
Neste problema, queremos calcular o número de produtos distintos que podem ser obtidos ao escolher 3 fatores distintos do conjunto {2, 3, 5, 7, 11}. Como a ordem dos fatores não importa (o produto será o mesmo independentemente da ordem), usamos o conceito de combinação.
2 – Entendendo o enunciado
- O conjunto dos fatores disponíveis é {2, 3, 5, 7, 11}, com n = 5 elementos.
- Precisamos escolher k = 3 elementos para formar os produtos.
- O número de combinações possíveis é dado pela fórmula:
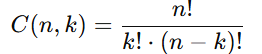
3 – Cálculo
Substituímos n = 5 e k = 3 na fórmula:
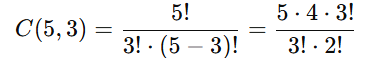
Cancelamos 3!3! no numerador e denominador:
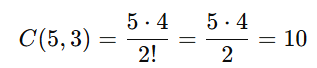
Portanto, há 10 combinações possíveis. Cada combinação representa um produto único porque os fatores são primos e distintos.
4 – Resposta
O número de produtos distintos que podem ser obtidos ao escolher 3 fatores diferentes do conjunto {2, 3, 5, 7, 11} é 10.
Gostou dessa questão de? Que tal desafiar ainda mais seus conhecimentos acessando mais uma questão matemática? 📚✨
📘 Quer dominar a análise combinatória? Adquira agora nosso PDF completo com exercícios resolvidos passo a passo e eleve seu aprendizado!
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉 Leia o artigo completo aqui!
