Como calcular a área de um setor circular
Aprenda a calcular a área de um setor circular usando a relação entre o raio e o comprimento do arco.
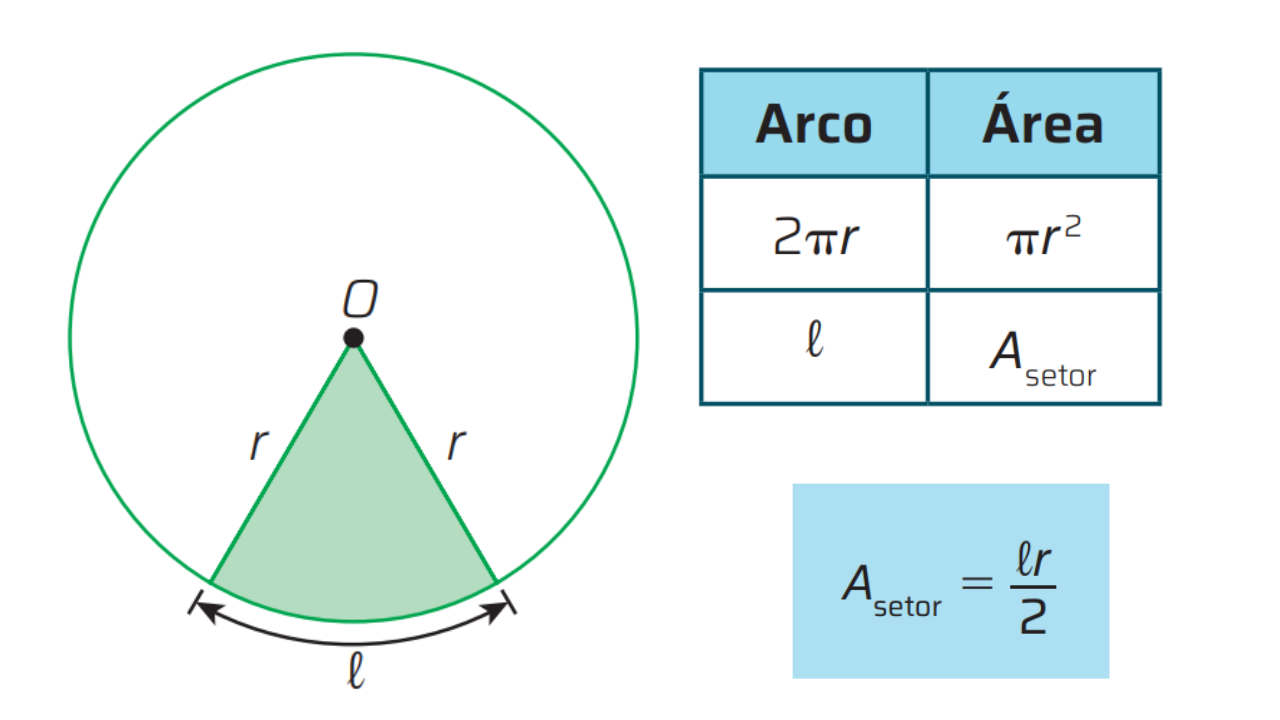
1) Conceito de setor circular
O setor circular é a região de um círculo delimitada por dois raios e um arco. Imagine uma fatia de pizza: o ponto central é o centro do círculo, os dois lados retos são os raios e a borda curva é o arco.
2) Fórmula da área usando o arco
Se conhecemos o comprimento do arco \(\ell\) e o raio \(r\), a área do setor pode ser calculada diretamente por:
Essa fórmula é prática porque não exige o ângulo central. Basta conhecer o arco e o raio.
3) Relação com o círculo inteiro
Quando o arco é toda a circunferência, temos:
Assim, a fórmula \(A_{\text{setor}}=\dfrac{\ell r}{2}\) se ajusta perfeitamente ao caso geral, já que:
\(A=\dfrac{(2\pi r)\cdot r}{2}=\pi r^2\).
4) Exemplos resolvidos
Exemplo 1: Em um círculo de raio \(r=6\) cm, o arco mede \(\ell=5\) cm. Calcule a área do setor.
Mostrar solução
\(A=\dfrac{\ell r}{2}=\dfrac{5\cdot6}{2}=15\;\text{cm}^2\).
Exemplo 2: Um setor tem raio \(r=10\) m e arco \(\ell=12\) m. Determine a área.
Mostrar solução
\(A=\dfrac{\ell r}{2}=\dfrac{12\cdot10}{2}=60\;\text{m}^2\).
5) Exercícios práticos
1. Um círculo tem raio \(r=8\) cm e arco \(\ell=6\) cm. A área do setor é:
Ver solução
\(A=\dfrac{6\cdot8}{2}=24\;\text{cm}^2\).
2. Se o arco mede \(\ell=15\) cm e o raio \(r=5\) cm, determine a área.
Ver solução
\(A=\dfrac{15\cdot5}{2}=37,5\;\text{cm}^2\).
6) Links relacionados
Dica: se souber o ângulo em radianos, use também a fórmula \(A=\tfrac{1}{2}r^2\alpha\).






















