Concavidade da parábola (função quadrática)

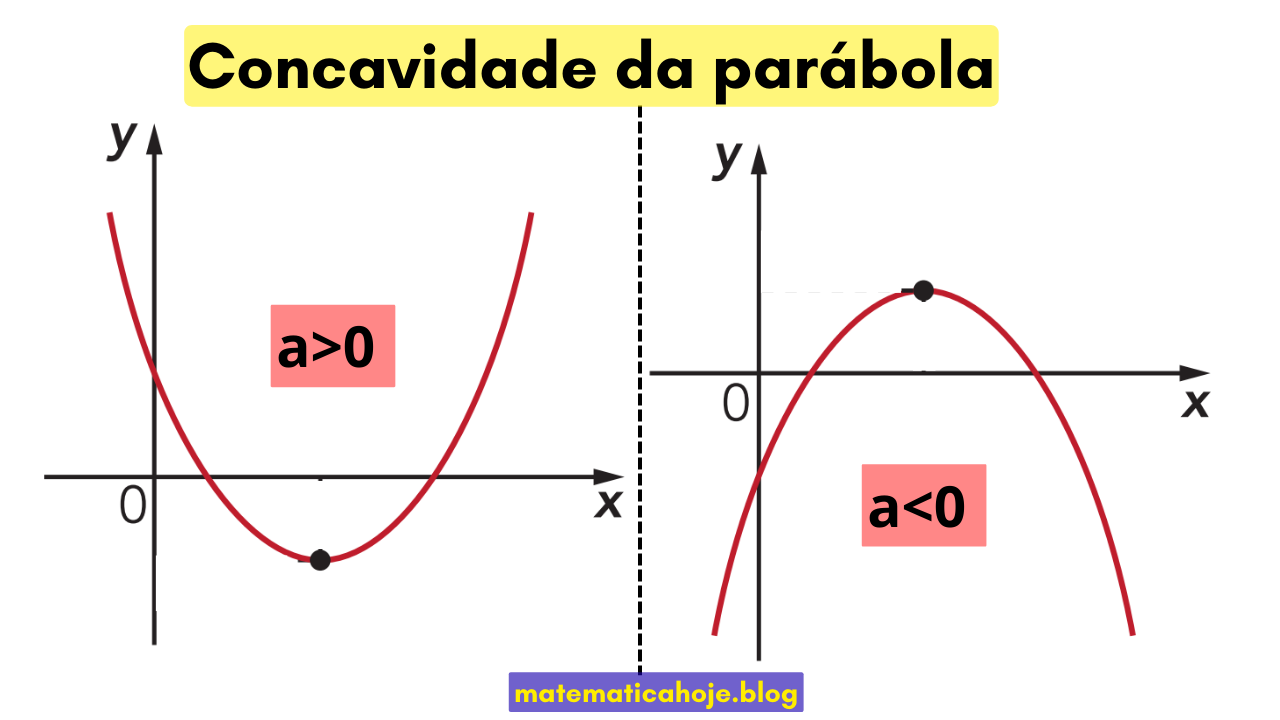
Para \(f(x)=ax^2+bx+c\), a concavidade depende do sinal de \(a\): \(a>0\Rightarrow\) abre para cima (vértice é mínimo); \(a<0\Rightarrow\) abre para baixo (vértice é máximo). Se precisar revisar o ponto \((0,c)\), veja: Intercepto no eixo y.

Concavidade da parábola: a>0 abre para cima e a<0 abre para baixo — Concavidade: \(a>0\Rightarrow\cup\) (mínimo) e \(a<0\Rightarrow\cap\) (máximo).

\[ \begin{aligned} &\textbf{Se } a>0:\ \text{parábola com concavidade para cima (vértice é mínimo).}\\ &\textbf{Se } a<0:\ \text{parábola com concavidade para baixo (vértice é máximo).} \end{aligned} \]

Critérios e links úteis

Pelo \(a\) (o mais rápido em provas).
Segunda derivada: \(f''(x)=2a\Rightarrow\) sinal de \(a\) decide.
Coeficiente \(a\): concavidade e abertura
Vértice: \(\big(-\frac{b}{2a},-\frac{\Delta}{4a}\big)\)

Exemplos resolvidos (contas em coluna)

Exemplo 1 — \(f(x)=2x^2-4x+1\)

Concavidade: \(a=2>0\Rightarrow\) para cima (mínimo).

\[ \begin{aligned} x_v &= -\frac{b}{2a}\\ &= -\frac{-4}{2\cdot 2}\\ &= -\frac{-4}{4}\\ &= 1 \end{aligned} \]

\[ \begin{aligned} f(1) &= 2\cdot 1^2 - 4\cdot 1 + 1\\ &= 2\\ &\ \ -4\\ &\ \ \ \ +1\\ &= -1 \end{aligned} \]

Logo, \(V(1,-1)\). Veja também: máximo e mínimo.

Exemplo 2 — \(g(x)=-3x^2+6x-5\)

Concavidade: \(a=-3<0\Rightarrow\) para baixo (máximo).

\[ \begin{aligned} x_v &= -\frac{b}{2a}\\ &= -\frac{6}{2\cdot (-3)}\\ &= -\frac{6}{-6}\\ &= 1 \end{aligned} \]

\[ \begin{aligned} g(1) &= -3\cdot 1^2 + 6\cdot 1 - 5\\ &= -3\\ &\ \ +6\\ &\ \ \ \ -5\\ &= -2 \end{aligned} \]

Vértice \(V(1,-2)\). Relembre o gráfico em como construir o gráfico.

Mais conexões

Função quadrática: guia completo Pontos notáveis da parábola Efeito de \(b\) e \(c\) A parábola: foco, diretriz e eixo

Exercícios

1) (Aberto) Para \(p(x)=-\tfrac14x^2+3x-1\), classifique a concavidade e determine o vértice.

Mostrar solução

\(a=-\tfrac14<0\Rightarrow\) concavidade para baixo (vértice é máximo).

\[ \begin{aligned} x_v &= -\frac{b}{2a}\\ &= -\frac{3}{2\cdot(-\tfrac14)}\\ &= -\frac{3}{-\tfrac12}\\ &= 6 \end{aligned} \]

\[ \begin{aligned} p(6) &= -\tfrac14\cdot 36 + 3\cdot 6 - 1\\ &= -9\\ &\ \ +18\\ &\ \ \ \ -1\\ &= 8 \end{aligned} \]

Vértice \(V(6,8)\).

2) (Aberto) Em \(q(x)=0{,}2x^2-2x+5\), classifique a concavidade, calcule o eixo de simetria e o valor de \(q(x_v)\).

Mostrar solução

\(a=0{,}2>0\Rightarrow\) concavidade para cima (vértice é mínimo).

\[ \begin{aligned} x_v &= -\frac{b}{2a}\\ &= -\frac{-2}{2\cdot 0{,}2}\\ &= \frac{2}{0{,}4}\\ &= 5 \end{aligned} \]

\[ \begin{aligned} q(5) &= 0{,}2\cdot 25 - 2\cdot 5 + 5\\ &= 5\\ &\ \ -10\\ &\ \ \ \ +5\\ &= 0 \end{aligned} \]

Logo, \(V(5,0)\).

3) (Múltipla escolha) Qual função tem concavidade para cima?

A) \(-2x^2+5x-1\)
B) \(x^2-7x+3\)
C) \(-\dfrac12x^2-4x+9\)
D) \(-x^2+3\)

Ver gabarito e explicação

Resposta: B. Concavidade depende do sinal de \(a\). Em B, \(a=1>0\Rightarrow\) para cima. Nas demais, \(a<0\Rightarrow\) para baixo.

4) (Múltipla escolha) Qual função tem abertura mais fechada que \(y=x^2\)?

A) \(y=\tfrac12x^2\)
B) \(y=2x^2\)
C) \(y=-\tfrac34x^2\)
D) \(y=-\tfrac15x^2\)

Ver gabarito e explicação

Resposta: B e C. A abertura é mais fechada quando \(|a|>1\) (comparando com \(|1|\)). Em B, \(|a|=2>1\). Em C, \(|a|=\tfrac34<1\) — opa, cuidado! Vamos analisar corretamente:

Para fechar mais que \(x^2\), precisamos de \(|a|>1\).