Estudamos anteriormente quando uma função real de variável real é crescente em um intervalo e quando ela é decrescente. Estudaremos, agora, o comportamento da função quadrática em relação a crescimento e decrescimento.
Em determinado momento de uma coreografia de ginástica rítmica, uma bola é lançada ao solo verticalmente para cima. A altura \( h \) da bola em relação ao solo, em metro, varia de acordo com o tempo \( t \), em segundo, conforme a lei \( h(t) = -5t^2 + 10t \), considerando \( 0 \leq t \leq 2 \).
Observe o gráfico que representa a função \( h \):
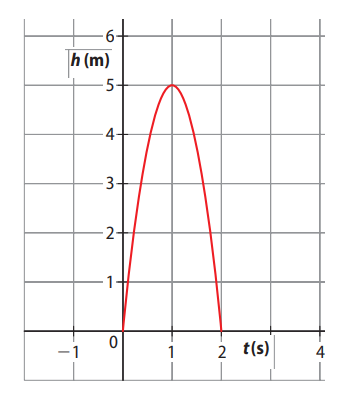
A função \( h \) é crescente no intervalo \( [0, 1] \), pois, à medida que \( t \) aumenta nesse intervalo, \( h(t) \) também aumenta.
Já a função \( h \) é decrescente no intervalo \( [1, 2] \), pois, à medida que \( t \) aumenta nesse intervalo, \( h(t) \) diminui.
De modo geral, podemos estudar o crescimento e o decrescimento da função quadrática definida por \( f(x) = ax^2 + bx + c \) com base no valor de a e na abscissa \( x_v \) do vértice da parábola, como indicado a seguir:
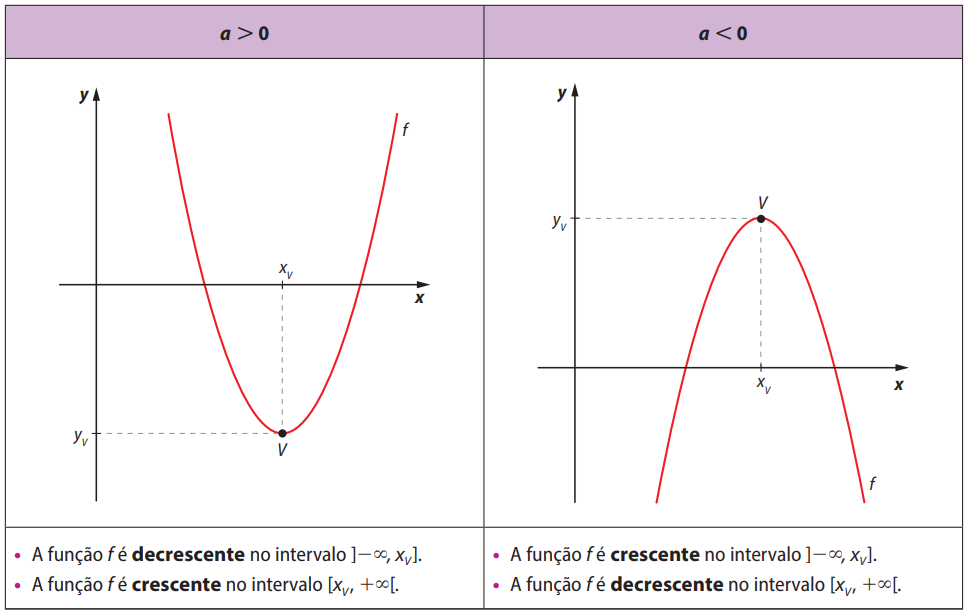
- Se \( a > 0 \), a função é decrescente no intervalo \( (-\infty, x_v] \) e crescente no intervalo \( [x_v, +\infty) \).
- Se \( a < 0 \), a função é crescente no intervalo \( (-\infty, x_v] \) e decrescente no intervalo \( [x_v, +\infty) \).
Considere, por exemplo, a função definida por \( f(x) = x^2 – 4x + 3 \).
Calculando a abscissa \( x_v \) do vértice da parábola correspondente, temos:
\[ x_v = \frac{-b}{2a} = \frac{-(-4)}{2 \cdot 1} = \frac{4}{2} = 2 \]
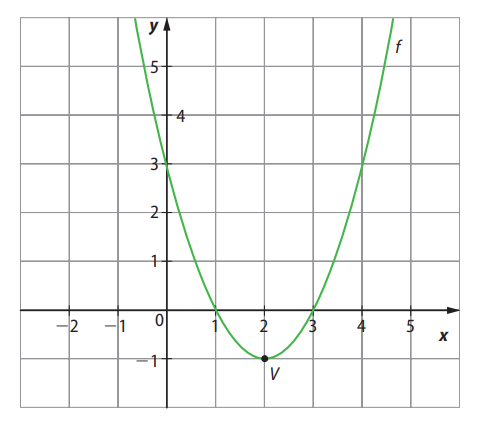
Assim, como \( a > 0 \), essa função é decrescente no intervalo \( (-\infty, 2) \) e crescente no intervalo \( (2, +\infty) \). Isso também pode ser observado por meio do gráfico a seguir:
Exercícios Resolvidos: Crescimento e Decrescimento da Função Quadrática
Questão 1: Considere a função quadrática definida por \( f(x) = -x^2 + 8x \). Determine em que intervalo ela é crescente.
▼ Solução da questão 1
Coeficientes: \( a = -1 \), \( b = 8 \).
Calculamos o x do vértice:
\[ x_v = \frac{-b}{2a} = \frac{-8}{2 \cdot (-1)} = \frac{-8}{-2} = 4 \]
Como \( a < 0 \), a função é:
- crescente no intervalo \( (-\infty, 4) \)
- decrescente no intervalo \( (4, +\infty) \)
Resposta: crescente em \( (-\infty, 4) \)
Questão 2: A função \( f(x) = x^2 – 6x + 2 \) é decrescente em qual intervalo?
▼ Solução da questão 2
Coeficientes: \( a = 1 \), \( b = -6 \).
Calculamos o x do vértice:
\[ x_v = \frac{-b}{2a} = \frac{-(-6)}{2 \cdot 1} = \frac{6}{2} = 3 \]
Como \( a > 0 \), a função é:
- decrescente no intervalo \( (-\infty, 3) \)
- crescente no intervalo \( (3, +\infty) \)
Resposta: decrescente em \( (-\infty, 3) \)
Questão 3: A função \( f(x) = 2x^2 + 4x + 1 \) é decrescente em que intervalo?
▼ Solução da questão 3
Coeficientes: \( a = 2 \), \( b = 4 \).
Calculamos o x do vértice:
\[ x_v = \frac{-b}{2a} = \frac{-4}{2 \cdot 2} = \frac{-4}{4} = -1 \]
Como \( a > 0 \), a função é:
- decrescente no intervalo \( (-\infty, -1) \)
- crescente no intervalo \( (-1, +\infty) \)
Resposta: decrescente em \( (-\infty, -1) \)
Questão 4: Em qual intervalo a função \( f(x) = -2x^2 + 2x – 5 \) é crescente?
▼ Solução da questão 4
Coeficientes: \( a = -2 \), \( b = 2 \).
Calculamos o x do vértice:
\[ x_v = \frac{-b}{2a} = \frac{-2}{2 \cdot (-2)} = \frac{-2}{-4} = \frac{1}{2} \]
Como \( a < 0 \), a função é:
- crescente no intervalo \( (-\infty, \frac{1}{2}) \)
- decrescente no intervalo \( (\frac{1}{2}, +\infty) \)
Resposta: crescente em \( (-\infty, \frac{1}{2}) \)
























