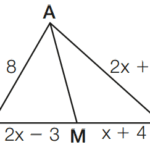Se tentássemos construir um triângulo de lados medindo a = 6 cm, b = 3 cm e c = 2 cm, obteríamos a figura ao lado. Os arcos não se cruzam.
Isso significa que não existe triângulo de lados medindo 6 cm, 3 cm e 2 cm.
Por que isso acontece? Esse fato é justificado pela propriedade a seguir:
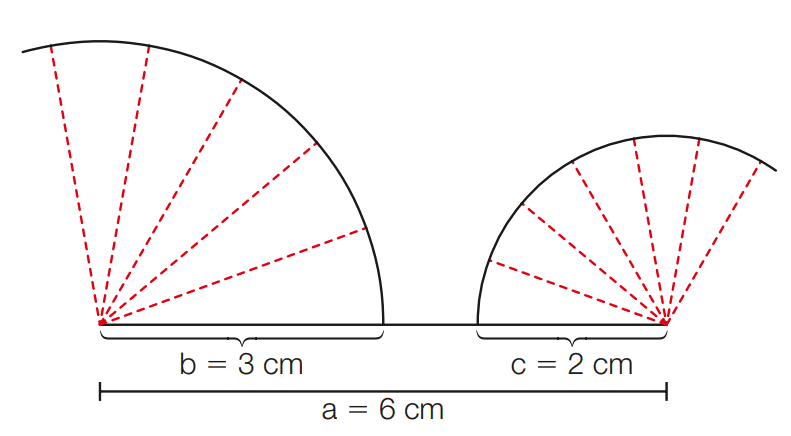
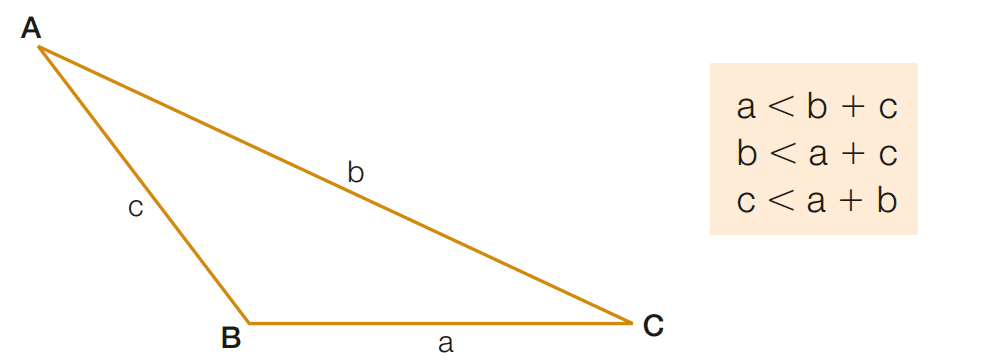
Então, dado o triângulo ABC, em que a é medida do lado BC, b é medida do lado AC e c é medida do lado AB, podemos escrever as seguintes relações:
Em qualquer triângulo, a medida de cada lado é menor que a soma das medidas dos outros dois lados.
Portanto, podemos saber se existe ou não um triângulo de determinadas medidas comparando a maior delas com a soma das outras duas. O triângulo só existirá se a medida do lado maior for menor que a soma das medidas dos outros dois.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Exemplo
Vamos verificar se existe um triângulo de lados medindo 9,2 cm, 13,1 cm e 4,7 cm.
Como a maior medida é 13,1 cm, vamos verificar a soma das outras duas medidas: 9,2 cm 1 4,7 cm 5 13,9 cm.
Como 13,1 < 13,9, existe um triângulo com essas medidas dos lados.
Exercício 1: Verifique se existe um triângulo com as seguintes medidas e justifique sua resposta:
a) 5 cm, 7 cm e 3 cm
b) 3 cm, 2 cm e 7 cm
c) 3 cm, 3 cm e 2 cm
d) 5 cm, 5 cm e 10 cm
e) 4 cm, 4 cm e 4 cm
f) 1 cm, 2 cm e 3 cm
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
a) Sim, pois o maior lado mede 7 cm e 7 < 5 + 3
b) Não, pois 7 não é menor que 2 + 3
c) Sim, pois o maior lado mede 3 cm e 3 < 3 + 2.
d) Não, pois 10 não é menor que 5 + 5.
e) Sim, pois o maior lado mede 4 cm e 4 < 4 + 4
f) Não, pois 3 não é menor que 1 + 2
[/toggle]
Exercício 2: Os lados de um triângulo medem, em centímetros, 5, 3 e x. Quais são os possíveis valores numéricos de x para que o triângulo exista?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Solução
Para que um triângulo exista, os lados devem satisfazer a desigualdade triangular, que afirma que a soma das medidas de dois lados de um triângulo deve ser sempre maior que o terceiro lado. No caso, os lados do triângulo são 5 cm, 3 cm e xxx. Vamos aplicar a desigualdade triangular nas três situações possíveis:
- 5 + 3 > x
- 5 + x > 3
- 3 + x > 5
Agora, vamos resolver essas desigualdades:
- 5 + 3 > x ⟹ 8 > x ⟹ x < 8
- 5 + x > 3 ⟹ x > −2 (Esta condição é sempre verdadeira, pois x é uma medida positiva)
- 3 + x > 5 ⟹ x > 2
Portanto, combinando as duas condições relevantes x < 8 e x > 2, o valor de x deve estar no intervalo:
2 < x < 8
Ou seja, os valores possíveis de xxx para que o triângulo exista são valores maiores que 2 e menores que 8.
[/toggle]
Exemplo 3: O triângulo ABC é isósceles de base BC. Sabendo que AB = 2x – 7 e AC = x + 5, determine x.
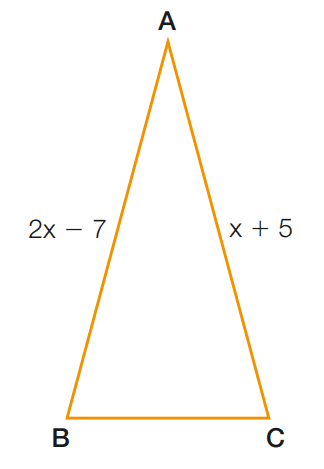
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Solução
Como o triângulo ABC é isósceles e tem a base BC, isso significa que os lados AB e AC são congruentes (iguais). Portanto, podemos igualar as expressões dadas para AB e AC para encontrar o valor de x.
As medidas dos lados são:
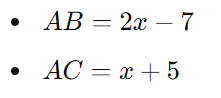
Como AB=AC, temos a equação:
2x − 7= x + 5
Agora, vamos resolver essa equação:
2x − x = 5 + 7
x = 12
Portanto, o valor de x é 12.
[/toggle]
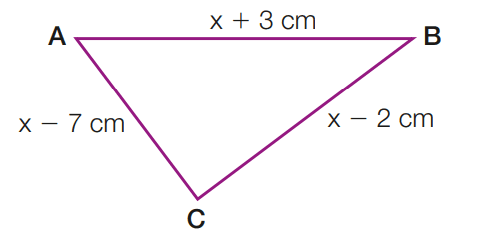
Exemplo 4: Determine as medidas do maior lado do triângulo da figura, sabendo que o perímetro é 60 cm.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Solução
Para determinar as medidas dos lados do triângulo e encontrar o maior lado, vamos utilizar as informações fornecidas na imagem e a condição de que o perímetro do triângulo é 60 cm.
Os lados do triângulo são:

Sabemos que o perímetro de um triângulo é a soma de seus lados, e o perímetro fornecido é 60 cm. Logo, temos a seguinte equação:
(x − 7) + (x − 2) + (x + 3) = 60
Agora, vamos resolver essa equação:
x − 7 + x − 2 + x + 3 = 60
3x − 6 = 60
3x = 66
x = 66/3
x = 22
Agora que encontramos o valor de x, podemos calcular o comprimento de cada lado:

Portanto, as medidas dos lados do triângulo são 15 cm, 20 cm e 25 cm. O maior lado é 25 cm.
[/toggle]
Leia também…