Se você é estudante ou concurseiro, provavelmente já se deparou com a dificuldade que a matemática pode apresentar. Entre os diversos tópicos, a função do segundo grau é um dos que mais gera dúvidas. Mas calma, você não está sozinho nessa! Com o auxílio do Bongo Quadrático, dominar esse conteúdo se tornará uma tarefa muito mais acessível e até divertida.
O que é a Função do Segundo Grau?
A função do segundo grau é representada pela fórmula:

onde ( a ), ( b ) e ( c ) são constantes, e ( a ≠ 0 ). Essa função forma uma parábola quando representada graficamente, podendo abrir para cima (quando ( a > 0 )) ou para baixo (quando ( a < 0 )).
Principais Elementos da Função
- Vértice: O ponto que representa o mínimo ou máximo da parábola.
- Raízes: Os valores de ( x ) que tornam a função igual a zero, ou seja, onde a parábola cruza o eixo ( x ).
- Eixo de Simetria: A linha vertical que passa pelo vértice e divide a parábola em duas partes iguais.
Como o Bongo Quadrático Facilita o Aprendizado?
O Bingo Quadrático é uma ferramenta inovadora que oferece diversos recursos para facilitar a compreensão da função do segundo grau. Aqui estão algumas maneiras de como ele pode ser útil:
- Visualização Interativa: O Bongo Quadrático permite que você altere os coeficientes ( a ), ( b ) e ( c ) e veja em tempo real como isso afeta a forma da parábola. Essa visualização ajuda a internalizar como cada variável impacta o gráfico.
- Exercícios Práticos: A plataforma oferece exercícios práticos que vão desde encontrar raízes até calcular o vértice. Você pode praticar e aplicar o que aprendeu de maneira divertida e interativa.
- Simulações e Jogos: O Bongo Quadrático inclui simulações e jogos que tornam o aprendizado mais dinâmico. Esses elementos lúdicos ajudam a fixar o conteúdo de forma mais eficiente.

Exemplos para Praticar
Vamos ver como usar o Bongo Quadrático em dois exemplos práticos:
Exemplo 1: Resolvendo a Equação Quadrática
Suponha que você tenha a função:

Com o Bongo Quadrático, você pode determinar as raízes utilizando a fórmula de Bhaskara:
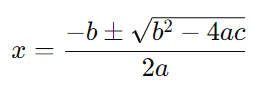
Aqui, ao inserir os valores de ( a ), ( b ) e ( c ), você verá como o gráfico muda conforme você ajusta esses coeficientes.
Exemplo 2: Encontrando o Vértice
Considere a função:

Você pode usar o Bongo Quadrático para calcular o vértice da parábola. O vértice pode ser encontrado com as coordenadas:

Após encontrar ( xv ), substitua-o na função para encontrar ( yv ).
Dicas para Aprofundar o Conhecimento
- Pratique com Frequência: A prática é essencial para entender a função do segundo grau. Use o Bongo Quadrático regularmente para resolver problemas variados.
- Discuta em Grupo: Aprender com outras pessoas pode ser muito enriquecedor. Troque ideias e resolva problemas em grupo.
- Refaça Exercícios: Ao errar, não desanime. Refazer os exercícios ajudará a fixar o conteúdo e a compreender onde errou.
Conclusão
Com a função do segundo grau, você tem uma ferramenta poderosa à sua disposição. O Bingo Quadrático torna o aprendizado mais interativo e prazeroso, ajudando a esclarecer as dúvidas que surgem ao longo do caminho. Então, não hesite em explorar essa ferramenta e transformar a maneira como você estuda matemática. Aprender pode ser divertido e, com o Bongo Quadrático, você vai perceber que a função do segundo grau não precisa ser um bicho de sete cabeças!

























