Dízima Periódica — como identificar, classificar e converter em fração (com exemplos e exercícios)
Guia prático e atualizado sobre dízimas periódicas (simples e composta), com passo a passo para transformar número decimal em fração, dicas para ENEM e concursos e uma lista de exercícios resolvidos.
Perfeito para revisar dízimas periódicas, frações, porcentagem e muito mais.
O que é dízima periódica?
Dízima periódica é um número decimal cujo(s) dígito(s) após a vírgula se repetem indefinidamente. Esse bloco que se repete é chamado de período. Exemplos: \(0,\overline{3} = 0{,}333\ldots\), \(1,\overline{27} = 1{,}272727\ldots\).
dízima periódica • dízima simples • dízima composta • como transformar dízima em fração • números decimais periódicos • período da dízima • repetição decimal • frações e decimais • exercícios de dízima • matemática básica
Tipos mais cobrados
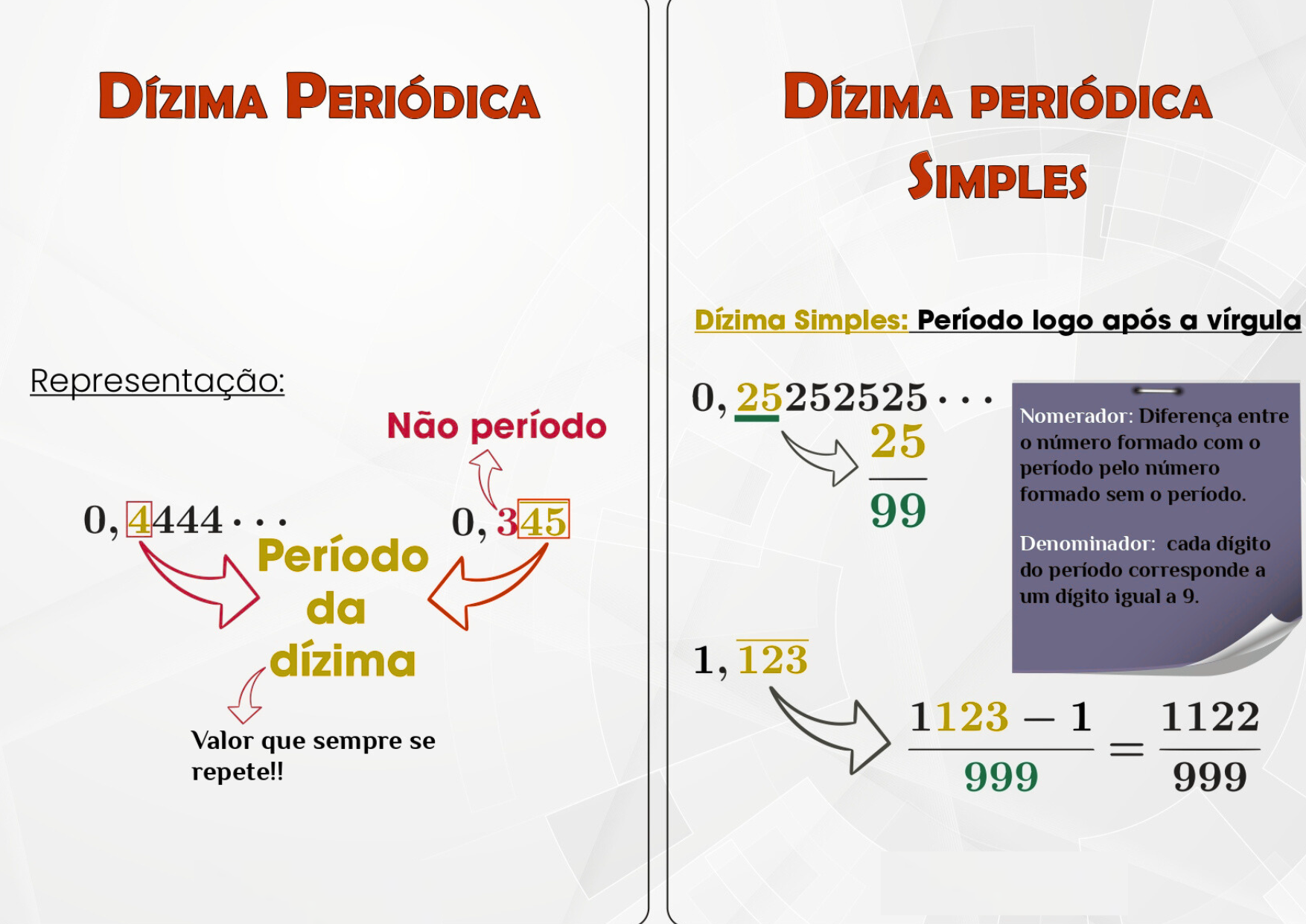
- Dízima periódica simples: o período aparece logo após a vírgula. Ex.: \(0,\overline{25}\).
- Dízima periódica composta: existe uma parte não periódica entre a vírgula e o período. Ex.: \(0,3\overline{45}\).
Como transformar dízima periódica em fração
Se \(x = 0,\overline{ab}\) (período com \(k\) dígitos), então:
fração \(\;\Rightarrow\; \displaystyle x=\frac{\text{número do período}}{\underbrace{99\ldots 9}_{k\ \text{noves}}}\).
Se \(x = 0,\text{(não-período)}\overline{\text{período}}\), então:
numerador: número formado por não-período+período menos o não-período.
denominador: tantos 9 quanto o período e tantos 0 quanto o não-período.
Dica: sempre que possível, reduza a fração ao menor termo.
Exemplos resolvidos (passo a passo)
Exemplo 1 — Dí zima simples: \(0,\overline{25}\) fácil
Ver solução
= \(\frac{25}{99}\)
= \(\frac{25}{99}\) (já está reduzida).
Exemplo 2 — Dí zima composta: \(0,3\overline{45}\) médio
Ver solução
Numerador: \(345 – 3 = 342\).
Denominador: como o período tem 2 dígitos → \(99\); como o não-período tem 1 dígito → um zero → \(990\).
\[ 0,3\overline{45}=\frac{342}{990} \] Simplificando por 18:
= \(\frac{342}{990}\)
= \(\frac{19}{55}\).
Exemplo 3 — Parte inteira + dízima: \(1,\overline{123}\)
Ver solução
= \(1 + \frac{41}{333}\)
= \(\frac{333}{333} + \frac{41}{333}\)
= \(\frac{374}{333}\).
Tenha as principais fórmulas (frações, decimais, porcentagem, juros, funções, geometria) organizadas para revisão rápida.
Perguntas rápidas (FAQ)
como identificar o período dízima é número racional? converter dízima em fração exercícios de dízima periódica
- Dízima periódica é racional? Sim. Toda dízima periódica é representável como fração \( \frac{p}{q} \) com \(q\neq 0\).
- Como achar o período? Observe o bloco que se repete. Em \(2,1\overline{04}\), o período é “04”.
- Que erros evit ar? Esquecer os zeros no denominador quando há parte não periódica.
Exercícios (com gabarito explicado)
1) Converta para fração: \(0,\overline{7}\).
Ver solução
= \(\frac{7}{9}\)
2) Converta para fração: \(0,\overline{142}\).
Ver solução
= \(\frac{142}{999}\)
= \(\frac{142}{999}\) (já está reduzida).
3) Converta para fração: \(0,6\overline{3}\).
Ver solução
Numerador: \(63-6=57\).
Denominador: um 9 (período) e um 0 (não-período) → \(90\).
= \(\frac{57}{90}\)
= \(\frac{19}{30}\).
4) Escreva \(1,\overline{6}\) como fração e simplifique.
Ver solução
= \(1 + \frac{2}{3}\)
= \(\frac{3}{3} + \frac{2}{3}\)
= \(\frac{5}{3}\).
5) Transforme \(2,4\overline{18}\) em fração.
Ver solução
Construa números: 2418 e 24.
Numerador: \(2418-24=2394\).
Denominador: dois 9 (período) e um zero (não-período) → \(990\).
Parte decimal: \(\frac{2394}{990}=\frac{399}{165}=\frac{133}{55}\).
= \(2 + \frac{133}{55}\)
= \(\frac{110}{55} + \frac{133}{55}\)
= \(\frac{243}{55}\).
6) (Múltipla escolha) A fração equivalente a \(0,\overline{81}\) é:
- A) \(\frac{8}{10}\)
- B) \(\frac{81}{99}\)
- C) \(\frac{9}{11}\)
- D) \(\frac{27}{33}\)
Ver solução
= Alternativa C.
7) (Desafio) Determine a soma \(S=0,\overline{3}+0,\overline{6}+0,\overline{9}\).
Ver solução
= \(\frac{1}{3}+\frac{2}{3}+1\)
= \(1+1\)
= \(2\).













