Conteúdo: Domínio e Imagem de Funções Reais
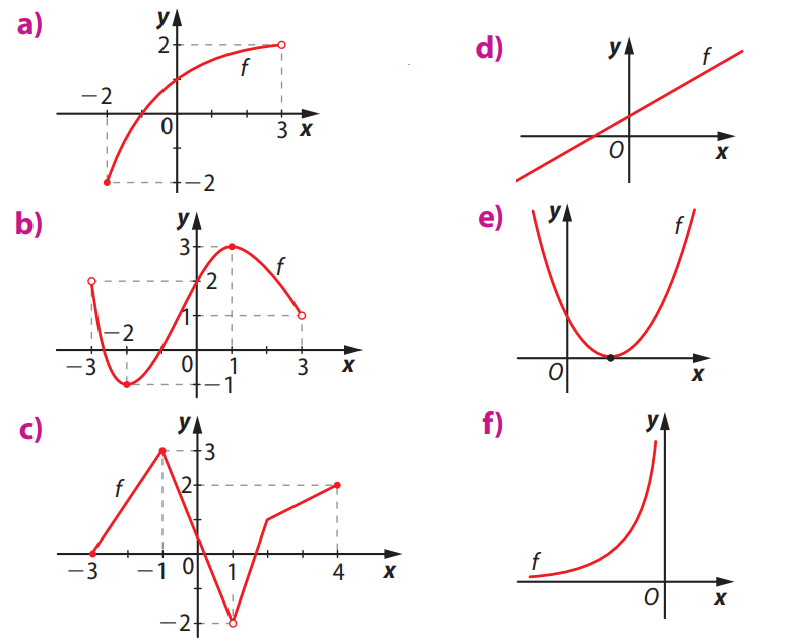
Questão 16. Os esboços dos gráficos a seguir representam funções reais de variável real. Observando-os, determine o domínio \( D(f) \) e o conjunto imagem \( \text{Im}(f) \) de cada função.
🔍 Ver solução passo a passo
Função a)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid -2 \leq x \leq 3 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid -2 \leq y \leq 2 \} $$
Função b)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid -3 < x < 3 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid -1 \leq y \leq 3 \} $$
Função c)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid -3 \leq x \leq 4 \text{ e } x \neq 1 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid -2 \leq y \leq 3 \} $$
Função d)
Domínio: $$ D(f) = \mathbb{R} $$
Imagem: $$ \text{Im}(f) = \mathbb{R} $$
Função e)
Domínio: $$ D(f) = \mathbb{R} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid y \geq 0 \} $$
Função f)
Domínio: $$ D(f) = \{ x \in \mathbb{R} \mid x < 0 \} $$
Imagem: $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid y > 0 \} $$
✅ Conclusão:
- Domínio refere-se aos valores possíveis para \( x \)
- Imagem refere-se aos valores resultantes de \( f(x) \)






















