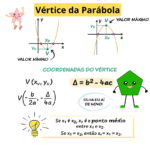
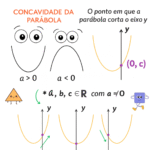
Equação do Segundo Grau: Fórmula de Bhaskara, Δ e Relações de Viète
A equação do segundo grau tem forma $$ ax^2 + bx + c = 0,\quad a\neq0, \; a,b,c\in\mathbb{R}. $$ Aqui você aprende a usar a fórmula de Bhaskara, interpretar o discriminante \( \Delta \) e aplicar as relações de soma e produto (Viète), com exemplos e exercícios.

1) Fórmula de Bhaskara (fórmula quadrática)
Discriminante: $$ \Delta = b^2 – 4ac. $$
Raízes: $$ x = \frac{-b \pm \sqrt{\Delta}}{2a}. $$
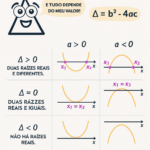
Casos de Δ
- \( \Delta > 0 \): duas raízes reais e distintas;
- \( \Delta = 0 \): uma raiz real dupla;
- \( \Delta < 0 \): sem raízes reais (complexas conjugadas).
2) Relações de Viète (soma e produto)
Se \(x_1\) e \(x_2\) são raízes, então: $$ x_1 + x_2 = -\frac{b}{a} \qquad \text{e} \qquad x_1\cdot x_2 = \frac{c}{a}. $$ Úteis para montar/checar equações e resolver sem calcular toda a fórmula.
Todas as fórmulas do Ensino Médio e Concursos em um único arquivo.
3) Exemplo resolvido
Resolva \( 2x^2 – 3x – 2 = 0 \).
- Coeficientes: \(a=2\), \(b=-3\), \(c=-2\).
- Δ: \( \Delta = (-3)^2 – 4\cdot2\cdot(-2) = 9 + 16 = 25 \).
- Bhaskara:
\( x = \dfrac{-(-3) \pm \sqrt{25}}{2\cdot2} \)
\( = \dfrac{3 \pm 5}{4} \)
\( \Rightarrow x_1 = 2,\; x_2 = -\dfrac{1}{2}. \) - Viète (checagem):
\( x_1+x_2 = 2 + \left(-\dfrac{1}{2}\right) = \dfrac{3}{2} = -\dfrac{b}{a} \)
\( x_1x_2 = 2\cdot\left(-\dfrac{1}{2}\right) = -1 = \dfrac{c}{a}. \)
📝 Exercícios — Equação do Segundo Grau
Inclui questões abertas e de múltipla escolha, com soluções em “abre/fecha”.
👀 Ver solução
Quem dita a quantidade de raízes reais é o discriminante \(\Delta=b^2-4ac\). Alternativa D.
👀 Ver solução
Produto \(x_1x_2=c/a=10\) e soma \(x_1+x_2=-b/a=7\). Pares (2,5) satisfazem. Alternativa A.
👀 Ver solução passo a passo
\(a=3,\; b=-12,\; c=9\)
\(\Delta = (-12)^2 – 4\cdot3\cdot9\)
\(= 144 – 108\)
\(= 36\)
\(x = \dfrac{-(-12) \pm \sqrt{36}}{2\cdot3}\)
\(= \dfrac{12 \pm 6}{6}\)
\(\Rightarrow x_1 = 3,\; x_2 = 1\).
👀 Ver solução
Para \(a=1\): \(b=-(x_1+x_2)=-4\) e \(c=x_1x_2=3\). Logo \(x^2-4x+3=0\). Alternativa A.
👀 Ver solução passo a passo
Produto \(x_1x_2=\dfrac{c}{a}=\dfrac{-12}{2}=-6\)
Soma \(x_1+x_2=\dfrac{-b}{a}=\dfrac{-5}{2}\)
Pares com produto \(-6\): \((-3,2)\), \((3,-2)\), \((6,-1)\), \((-6,1)\).
Que soma \(-\dfrac{5}{2}\)?
\(\;3+(-2)=1\) ❌
\((-3)+2=-1\) ❌
\(6+(-1)=5\) ❌
\((-6)+1=-5\) ✅ mas precisamos dividir por 2 (porque \(a\neq1\))? Não: as relações já consideram \(a\). Logo as raízes devem satisfazer Bhaskara; confirmando:
\(\Delta=5^2-4\cdot2\cdot(-12)=25+96=121\)
\(x=\dfrac{-5\pm \sqrt{121}}{2\cdot2}=\dfrac{-5\pm11}{4}\)
\(x_1=\dfrac{6}{4}=\dfrac{3}{2},\; x_2=\dfrac{-16}{4}=-4\)
Conferência: \(x_1+x_2=\dfrac{3}{2}-4=-\dfrac{5}{2}\) e \(x_1x_2=\dfrac{3}{2}\cdot(-4)=-6\).
👀 Ver solução
\(\Delta=b^2-4ac=b^2-4\cdot1\cdot16=b^2-64\). Para \(\Delta=0\): \(b^2=64\Rightarrow b=\pm8\). Alternativa A.
👀 Ver solução passo a passo
Substitua \(x=3\):
\(3^2 – 2\cdot3 + c = 0\)
\(= 9 – 6 + c\)
\(= 3 + c\)
\(\Rightarrow c = -3\).
👀 Ver solução
Raiz dupla ⇒ \(\Delta=0\).
\(\Delta=b^2-4ac=(-10)^2-4\cdot k \cdot 25=100-100k=0\Rightarrow k=1\). Alternativa B.
Links úteis para continuar
- Mapas Mentais de Matemática
- Matemática para o ENEM
- Coleção 10 eBooks
- Banco de Questões de Matemática
- eBook Fórmulas Matemática (PDF)
Compartilhe com a turma e salve este post para revisão! 💙