Exercício Pontos Notáveis do Triângulo

Nesta coleção de exercícios de pontos notáveis do triângulo você pratica baricentro, incentro, circuncentro e ortocentro com enunciados objetivos e soluções passo a passo (ótimas para celular). Se precisar revisar a teoria antes de resolver, consulte o guia Pontos Notáveis do Triângulo e os artigos específicos: medianas e baricentro (razão 2:1), bissetrizes internas e incentro (círculo inscrito), mediatrizes e circuncentro (círculo circunscrito) e alturas e ortocentro (posição por tipo de triângulo). Para mais prática, acesse também a lista completa de exercícios de pontos notáveis.

Exercício 1 – Classifique em verdadeiro (V) ou falso (F):

O incentro é o centro da circunferência inscrita no triângulo.
O circuncentro é o centro da circunferência circunscrita ao triângulo.
O incentro é interno ao triângulo.
O baricentro é interno ao triângulo.
O ortocentro é interno ao triângulo.
O circuncentro é interno ao triângulo.
O baricentro é o centro da circunferência inscrita no triângulo.

Ver solução

Use o guia Pontos Notáveis do Triângulo para revisar as definições.

a) V — O incentro é a interseção das bissetrizes internas e é o centro do círculo inscrito. Bissetrizes e Incentro.
b) V — O circuncentro é a interseção das mediatrizes dos lados e é o centro do círculo circunscrito. Mediatrizes e Circuncentro.
c) V — O incentro é sempre interno (equidistante dos lados). Saiba mais.
d) V — O baricentro (encontro das medianas) é sempre interno e divide cada mediana em 2:1. Medianas e Baricentro.
e) F — O ortocentro só é interno em triângulos acutângulos; em retângulos coincide com o vértice do ângulo reto e em obtusângulos fica externo. Alturas e Ortocentro.
f) F — O circuncentro é interno apenas em triângulos acutângulos; em retângulos está no meio da hipotenusa e em obtusângulos é externo. Revisar.
g) F — O centro da circunferência inscrita é o incentro, não o baricentro. Ver definição.

Gabarito: a) V, b) V, c) V, d) V, e) F, f) F, g) F.

Exercício 2 – Diga que triângulo satisfaz a condição dada nos casos:

O ortocentro e o baricentro são coincidentes;
O incentro e o circuncentro são coincidentes;
O ortocentro é um dos vértices;
O ortocentro é externo;
O circuncentro é externo;
O circuncentro está em um dos lados;
O ortocentro é um ponto interno.

Ver solução

a) Triângulo equilátero. Em equiláteros, todas as linhas notáveis coincidem: H = G = I = O. Guia geral.
b) Triângulo equilátero. Logo, incentro e circuncentro também coincidem. Incentro • Circuncentro.
c) Triângulo retângulo. O ortocentro é o próprio vértice do ângulo reto. Alturas e H.
d) Triângulo obtusângulo. Para ângulo obtuso, as alturas se interceptam fora: H externo. Posições de H.
e) Triângulo obtusângulo. O circuncentro (mediatrizes) fica externo. Revisar O.
f) Triângulo retângulo. O circuncentro é o ponto médio da hipotenusa (sobre um lado). Circuncentro no retângulo.
g) Triângulo acutângulo. Com todos os ângulos agudos, o ortocentro é interno. Ver mais.

Gabarito resumido: a) Equilátero • b) Equilátero • c) Retângulo • d) Obtusângulo • e) Obtusângulo • f) Retângulo • g) Acutângulo.

Exercício 3 – Considere os segmentos formados pelas três alturas, pelas três medianas e pelas três bissetrizes internas de um triângulo (total de até 9 segmentos). Quantos desses segmentos, dois a dois distintos, teremos:

no triângulo equilátero;
no triângulo isósceles não equilátero;
no triângulo escaleno.

Ver solução

Ideia-chave: coincidências entre linhas notáveis reduzem a contagem. Consulte os resumos: Pontos notáveis, Alturas, Medianas e Bissetrizes.

a) Equilátero → 3 segmentos. Em um triângulo equilátero, para cada vértice a altura coincide com a mediana e com a bissetriz. Assim, existem apenas os três segmentos que partem dos vértices (todos concorrentes no mesmo ponto), logo 3.
b) Isósceles não equilátero → 7 segmentos. A partir do vértice do ângulo entre os lados congruentes, a altura, a mediana e a bissetriz coincidem (um único segmento). Já em cada vértice da base, os três segmentos são distintos. Portanto:
- 1 segmento (vértice do topo) + 3 segmentos (vértice da base esquerda) + 3 segmentos (vértice da base direita) = 7.
c) Escaleno → 9 segmentos. Não há coincidências: em cada vértice, altura, mediana e bissetriz são diferentes. Logo, 3 × 3 = 9.

Gabarito: a) 3 • b) 7 • c) 9.

Exercício 4 – Sendo G o baricentro do triângulo ABC, determine x, y e z.
Dados: AG = 10, BG = y e CG = 14.

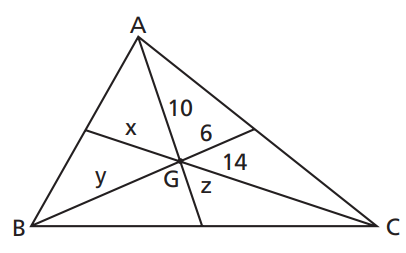
Triângulo ABC com medianas concorrendo em G; segmentos x, y e z

Ver solução

Fato do baricentro: em cada mediana, o baricentro divide o segmento na razão 2:1 (do vértice até G é o dobro do trecho de G ao ponto médio).

1) Mediana a partir de A (trechos AG e GM_BC; na figura, z é o trecho abaixo de G):

$$ \frac{AG}{GM_{BC}} = 2 $$
$$ GM_{BC} = \frac{AG}{2} $$
$$ GM_{BC} = \frac{10}{2} = 5 $$

Logo, z = 5.

2) Mediana a partir de B (trechos BG = y e GM_AC = x):

$$ \frac{BG}{GM_{AC}} = 2 $$
$$ y = 2x $$
$$ x = \frac{y}{2} $$

3) Mediana a partir de C (trechos CG = 14 e GM_AB):

$$ \frac{CG}{GM_{AB}} = 2 $$
$$ GM_{AB} = \frac{CG}{2} $$
$$ GM_{AB} = \frac{14}{2} = 7 $$

Resposta: z = 5, x = y/2 e y = 2x.

Reforce: Medianas e baricentro • Pontos notáveis do triângulo.

Exercício 5 – Se o quadrilátero ABCD é um paralelogramo e M é o ponto médio de AB, determine x.
Dados: DP = 16 e PM = x.

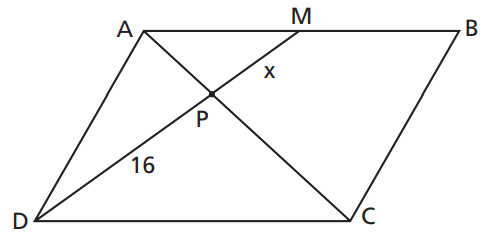
Paralelogramo ABCD com M ponto médio de AB; P interseção de DM com AC; DP=16 e PM=x

Ver solução

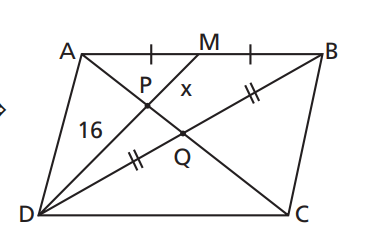
Construção auxiliar com diagonal BD e ponto Q, mostrando que P é o baricentro de ABD

Ideia: Transformar o problema em um caso de baricentro no triângulo ABD.

$$ \text{Trace a diagonal } BD \text{ e chame } Q \text{ o ponto de interseção das diagonais.} $$
$$ \text{Em um paralelogramo, as diagonais se bissetam } \Rightarrow Q \text{ é ponto médio de } BD. $$
$$ M \text{ é ponto médio de } AB \ (\text{dado}). $$
$$ \text{No } \triangle ABD,\ DM \text{ e } AQ \text{ são medianas e se cruzam em } P. $$
$$ \Rightarrow\ P \text{ é o baricentro de } \triangle ABD. $$
$$ \text{O baricentro divide a mediana na razão } 2:1 \ (\text{a partir do vértice}). $$
$$ \therefore\ DP = \frac{2}{3}DM \quad \text{e} \quad PM = \frac{1}{3}DM. $$
$$ \frac{DP}{PM} = \frac{ \frac{2}{3}DM }{ \frac{1}{3}DM } = 2 \ \Rightarrow\ PM = \frac{DP}{2}. $$
$$ PM = \frac{16}{2} = 8. $$

Resposta: x = 8.

Revisões úteis: Medianas e baricentro • Pontos notáveis do triângulo.

Exercício 6 – Sendo H o ortocentro de um triângulo ABC e ∠BHC = 150°, determine ∠A.

Ver solução

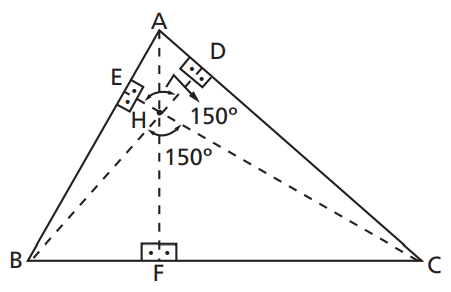
Solução: triângulo ABC com ortocentro H, pés das alturas D,E,F e marcações angulares

$$ \text{Sejam } D\in AC,\ E\in AB,\ F\in BC \text{ os pés das alturas.} $$
$$ \angle BHC = 150^\circ \ \Rightarrow\ \angle DHE = 150^\circ \ (\text{opostos pelo vértice}). $$
$$ \angle ADE = 90^\circ \ \text{e}\ \angle AHE = 90^\circ \ \Rightarrow\ A,D,H,E \text{ são concíclicos.} $$
$$ \text{Em quadrilátero cíclico, ângulos opostos somam } 180^\circ. $$
$$ \angle A + \angle DHE = 180^\circ \ \Rightarrow\ \angle A = 180^\circ – 150^\circ = 30^\circ. $$

Resposta: ∠A = 30°.

Exercício 7 – Se H é o ortocentro de um triângulo isósceles ABC de base BC e ∠BHC = 50°, determine os ângulos do triângulo.

Ver solução

$$ \text{Propriedade: } \angle BHC = 180^\circ – \angle A. $$
$$ 50^\circ = 180^\circ – \angle A \ \Rightarrow\ \angle A = 180^\circ – 50^\circ = 130^\circ. $$
$$ \text{Como } ABC \text{ é isósceles de base } BC,\ \angle B = \angle C. $$
$$ \angle A + \angle B + \angle C = 180^\circ \ \Rightarrow\ 130^\circ + 2\angle B = 180^\circ. $$
$$ 2\angle B = 50^\circ \ \Rightarrow\ \angle B = 25^\circ \ \Rightarrow\ \angle C = 25^\circ. $$

Resposta: ∠A = 130°, ∠B = 25°, ∠C = 25°.

Veja também: Alturas e ortocentro • Pontos notáveis do triângulo.

Exercício 8 – Se P é o incentro do triângulo ABC e ∠BPC = 125°, determine ∠A.

Ver solução

Fato conhecido do incentro: o ângulo formado pelas semirretas que ligam o incentro aos vértices B e C vale 90° + A/2.

$$ \angle BPC = 90^\circ + \frac{A}{2} $$
$$ 125^\circ = 90^\circ + \frac{A}{2} $$
$$ \frac{A}{2} = 35^\circ $$
$$ A = 70^\circ $$

Resposta: ∠A = 70°.

Revisão útil: Bissetrizes e incentro.

Exercício 9 – Em um triângulo ABC, os ângulos A e B medem, respectivamente, 86° e 34°. Determine o ângulo agudo formado pela mediatriz relativa ao lado BC e pela bissetriz do ângulo C.

Ver solução

$$ C = 180^\circ – (A+B) = 180^\circ – (86^\circ + 34^\circ) = 60^\circ $$
$$ \text{A bissetriz interna em } C \text{ forma } \frac{C}{2} = 30^\circ \text{ com } \overline{CB} \text{ e com } \overline{CA}. $$
$$ \text{A mediatriz de } BC \text{ é perpendicular a } BC. \text{ O ângulo entre retas não muda por translação.} $$
$$ \Rightarrow \text{O ângulo pedido }= \angle\big((\perp\ a\ BC \text{ por } C),\ \text{bissetriz em } C\big). $$
$$ \text{Esse ângulo} = 90^\circ – \frac{C}{2} = 90^\circ – 30^\circ = 60^\circ. $$

Resposta: 60°.

Revisões: Mediatrizes e circuncentro • Bissetrizes e incentro.

Relacionadas

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.