Questão 1. A trajetória de uma bola de futebol em uma cobrança de falta foi descrita por uma função quadrática que relaciona a altura \( h \) alcançada pela bola (em metros), em relação ao solo, e o deslocamento horizontal \( x \) da bola (em metros). Essa função é dada por:
$$ h(x) = -\frac{x^2}{60} + 0{,}5x $$
a) Qual é a distância entre o ponto em que a bola sai do solo e o ponto em que a bola toca novamente o solo?
b) Qual é a altura máxima atingida pela bola nessa trajetória?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Estamos lidando com uma função quadrática que representa uma parábola voltada para baixo. Precisamos encontrar:
- As raízes da função para saber onde a bola toca o solo.
- O valor máximo da função para descobrir a altura máxima atingida.
1) Encontrar os valores de \( x \) para \( h(x) = 0 \):
$$ h(x) = -\frac{x^2}{60} + 0{,}5x $$
$$ -\frac{x^2}{60} + 0{,}5x = 0 $$
$$ x \left( -\frac{x}{60} + 0{,}5 \right) = 0 $$
$$ x = 0 \quad \text{ou} \quad -\frac{x}{60} + 0{,}5 = 0 $$
$$ \frac{x}{60} = 0{,}5 $$
$$ x = 30 $$
Distância entre os pontos: 30 metros
2) Calcular a altura máxima (vértice da parábola):
$$ x_v = -\frac{b}{2a} $$
$$ a = -\frac{1}{60}, \quad b = 0{,}5 $$
$$ x_v = -\frac{0{,}5}{2 \cdot \left(-\frac{1}{60}\right)} $$
$$ x_v = \frac{0{,}5}{\frac{2}{60}} $$
$$ x_v = \frac{0{,}5 \cdot 60}{2} $$
$$ x_v = \frac{30}{2} = 15 $$
Substituindo em \( h(x) \):
$$ h(15) = -\frac{15^2}{60} + 0{,}5 \cdot 15 $$
$$ h(15) = -\frac{225}{60} + 7{,}5 $$
$$ h(15) = -3{,}75 + 7{,}5 $$
$$ h(15) = 3{,}75 $$
✅ Conclusão:
- a) Distância total: $$30\ \text{metros}$$
- b) Altura máxima: $$3{,}75\ \text{metros}$$
Questão 2. Faça um esboço do gráfico das funções quadráticas a seguir. Indique o vértice da parábola, o ponto de interseção da parábola com o eixo y e, se existirem, os zeros da função:
a) \( y = x^2 – 5x + 6 \)
b) \( y = -x^2 + 4 \)
c) \( y = x^2 – 4x + 4 \)
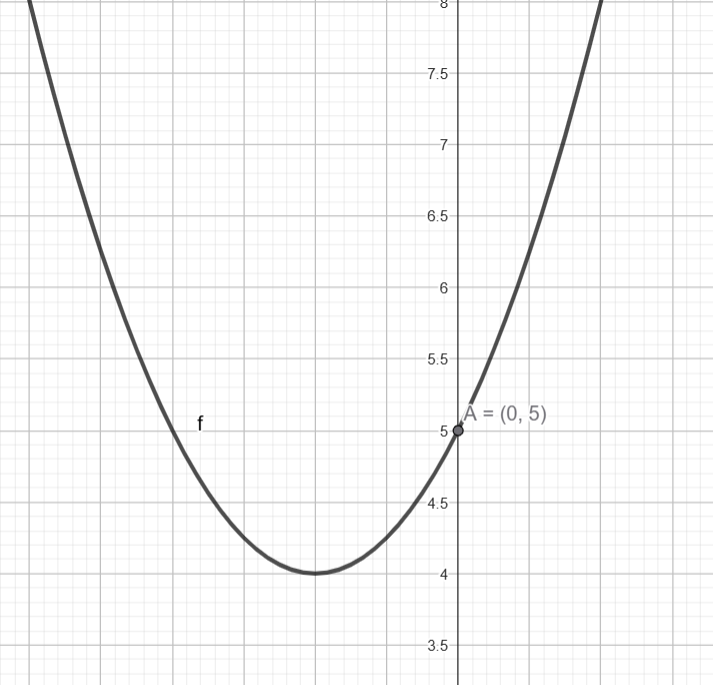
d) \( y = x^2 + 2x + 5 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos identificar para cada função quadrática: o vértice (máximo ou mínimo da parábola), o ponto de interseção com o eixo \( y \) (quando \( x = 0 \)), e os zeros da função (valores de \( x \) para os quais \( y = 0 \)).
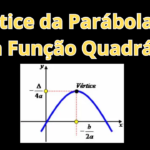
1) Analisando a função a) \( y = x^2 – 5x + 6 \)
$$ a = 1,\ b = -5,\ c = 6 $$
$$ x_v = -\frac{-5}{2 \cdot 1} = \frac{5}{2} = 2{,}5 $$
$$ y_v = (2{,}5)^2 – 5 \cdot 2{,}5 + 6 = 6{,}25 – 12{,}5 + 6 = -0{,}25 $$
Vértice: \( (2{,}5,\ -0{,}25) \)
$$ y(0) = 6 \quad \text{(interseção com o eixo } y\text{)} $$
$$ \Delta = (-5)^2 – 4 \cdot 1 \cdot 6 = 25 – 24 = 1 $$
$$ x = \frac{5 \pm \sqrt{1}}{2} = \frac{5 \pm 1}{2} $$
$$ x_1 = 3,\quad x_2 = 2 $$
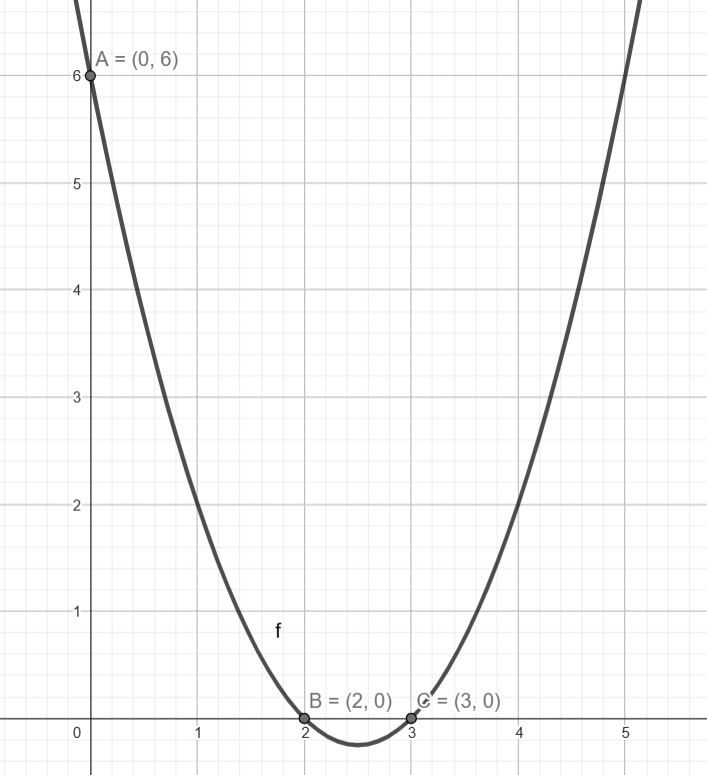
2) Analisando a função b) \( y = -x^2 + 4 \)
$$ a = -1,\ b = 0,\ c = 4 $$
$$ x_v = 0,\quad y_v = -0^2 + 4 = 4 $$
Vértice: \( (0,\ 4) \)
$$ y(0) = 4 \quad \text{(interseção com o eixo } y\text{)} $$
$$ -x^2 + 4 = 0 \Rightarrow x^2 = 4 \Rightarrow x = \pm 2 $$
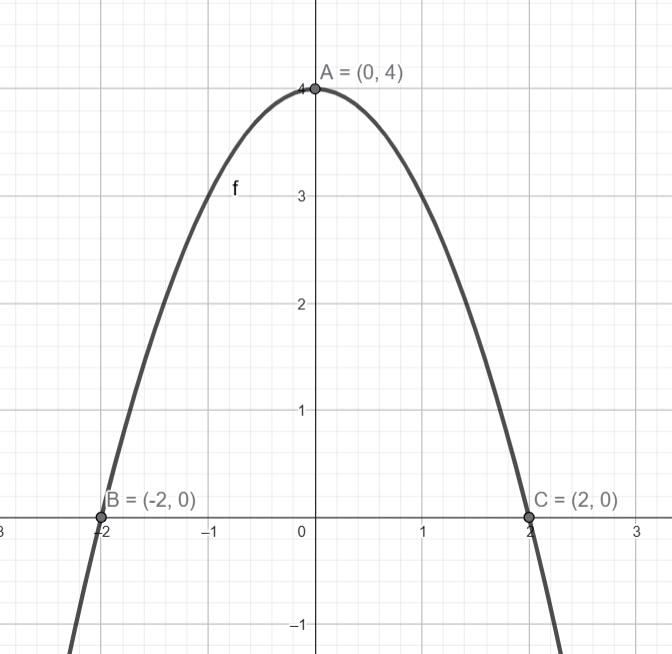
3) Analisando a função c) \( y = x^2 – 4x + 4 \)
$$ a = 1,\ b = -4,\ c = 4 $$
$$ x_v = -\frac{-4}{2 \cdot 1} = 2 $$
$$ y_v = 2^2 – 4 \cdot 2 + 4 = 4 – 8 + 4 = 0 $$
Vértice: \( (2,\ 0) \)
$$ y(0) = 4 \quad \text{(interseção com o eixo } y\text{)} $$
$$ \Delta = (-4)^2 – 4 \cdot 1 \cdot 4 = 16 – 16 = 0 $$
Raiz dupla: \( x = 2 \)
4) Analisando a função d) \( y = x^2 + 2x + 5 \)
$$ a = 1,\ b = 2,\ c = 5 $$
$$ x_v = -\frac{2}{2 \cdot 1} = -1 $$
$$ y_v = (-1)^2 + 2 \cdot (-1) + 5 = 1 – 2 + 5 = 4 $$
Vértice: \( (-1,\ 4) \)
$$ y(0) = 5 \quad \text{(interseção com o eixo } y\text{)} $$
$$ \Delta = 2^2 – 4 \cdot 1 \cdot 5 = 4 – 20 = -16 $$
Não possui raízes reais
✅ Conclusão:
- Letra a: Vértice \( (2{,}5,\ -0{,}25) \), raízes \( x = 2 \) e \( x = 3 \), interseção \( y = 6 \)
- Letra b: Vértice \( (0,\ 4) \), raízes \( x = -2 \) e \( x = 2 \), interseção \( y = 4 \)
- Letra c: Vértice \( (2,\ 0) \), raiz dupla \( x = 2 \), interseção \( y = 4 \)
- Letra d: Vértice \( (-1,\ 4) \), sem raízes reais, interseção \( y = 5 \)
Questão 3. Determine o conjunto imagem das funções quadráticas definidas a seguir:
a) \( f(x) = 3x^2 – 2x – 1 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Para encontrar o conjunto imagem de uma função quadrática, analisamos a concavidade da parábola e o valor do vértice (mínimo ou máximo da função).
1) Analisando a função \( f(x) = 3x^2 – 2x – 1 \)
Coeficientes: \( a = 3,\ b = -2,\ c = -1 \)
Como \( a > 0 \), a parábola tem concavidade voltada para cima → possui valor mínimo.
Calculando o vértice:
$$ x_v = -\frac{-2}{2 \cdot 3} = \frac{2}{6} = \frac{1}{3} $$
Substituindo em \( f(x) \):
$$ f\left(\frac{1}{3}\right) = 3 \cdot \left(\frac{1}{3}\right)^2 – 2 \cdot \frac{1}{3} – 1 $$
$$ = 3 \cdot \frac{1}{9} – \frac{2}{3} – 1 = \frac{1}{3} – \frac{2}{3} – 1 = -\frac{1}{3} – 1 = -\frac{4}{3} $$
Imagem: \( \text{Im}(f) = \{ y \in \mathbb{R} \mid y \geq -\frac{4}{3} \} \)
2) Analisando a função \( g(x) = -2x^2 + 1 \)
Coeficientes: \( a = -2,\ b = 0,\ c = 1 \)
Como \( a < 0 \), a parábola tem concavidade voltada para baixo → possui valor máximo.
$$ x_v = -\frac{0}{2 \cdot (-2)} = 0 $$
$$ g(0) = -2 \cdot 0^2 + 1 = 1 $$
Imagem: \( \text{Im}(g) = \{ y \in \mathbb{R} \mid y \leq 1 \} \)
✅ Conclusão:
- Função f(x): $$ \text{Im}(f) = \{ y \in \mathbb{R} \mid y \geq -\frac{4}{3} \} $$
- Função g(x): $$ \text{Im}(g) = \{ y \in \mathbb{R} \mid y \leq 1 \} $$
Questão 4. Murilo comprou 40 metros de cerca para fazer um cercado em formato de retângulo para seu cachorro no quintal de sua moradia. Ele vai aproveitar uma parede como um dos lados do cercado, de acordo com a figura a seguir:
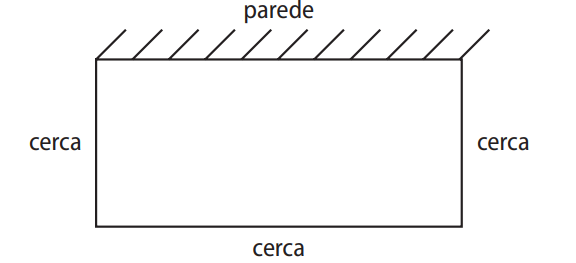
Sabendo que ele vai utilizar toda a cerca comprada, qual é a área máxima que esse cercado poderá ter?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos um retângulo com um lado encostado na parede, ou seja, ele usará a cerca apenas em 3 lados: 2 lados menores (largura) e 1 lado maior (comprimento).
Seja \( x \) a largura do cercado e \( y \) o comprimento (paralelo à parede).
1) Relacionar o perímetro com a cerca disponível:
$$ 2x + y = 40 \Rightarrow y = 40 – 2x $$
2) Escrever a função da área:
$$ A(x) = x \cdot y = x(40 – 2x) $$
$$ A(x) = 40x – 2x^2 $$
3) Encontrar o valor de \( x \) que fornece a área máxima:
$$ x_v = -\frac{b}{2a} = -\frac{40}{2 \cdot (-2)} = \frac{40}{4} = 10 $$
4) Calcular a área máxima:
$$ y = 40 – 2 \cdot 10 = 20 $$
$$ A = 10 \cdot 20 = 200\ m^2 $$
✅ Conclusão:
- Área máxima do cercado: $$ 200\ m^2 $$
Questão 5. (UFJF-MG) Sobre os lados do retângulo \(ABCD\), de dimensões 30 cm e 50 cm, marcam-se os pontos \(M\), \(N\), \(P\) e \(Q\) de forma que a distância dos pontos \(M\) e \(N\) ao vértice \(A\) e dos pontos \(P\) e \(Q\) ao vértice \(C\) sejam iguais a \(x\) centímetros. Veja a figura:
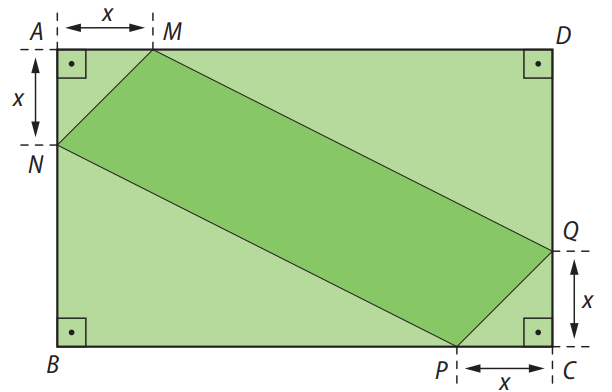
Determine o valor de \(x\) de modo que o quadrilátero \(MNQP\) tenha área máxima.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Os pontos \(M\), \(N\), \(P\) e \(Q\) são marcados a uma distância \(x\) das extremidades dos vértices do retângulo. Desejamos determinar a área máxima da região em verde (quadrilátero \(MNQP\)), que pode ser obtida pela subtração da área de dois triângulos dos cantos da área total do retângulo.
1) Área do retângulo total:
$$ A_{\text{total}} = 30 \cdot 50 = 1500\ \text{cm}^2 $$
2) Área da região MNQP:
A região MNQP é o retângulo menos dois triângulos idênticos formados nos cantos com catetos \(x\) e \(50 – 2x\).
Área de um triângulo:
$$ A_{\text{triângulo}} = \frac{x(50 – 2x)}{2} $$
Área total dos dois triângulos:
$$ A_{\text{triângulos}} = 2 \cdot \frac{x(50 – 2x)}{2} = x(50 – 2x) $$
Logo, a área do quadrilátero MNQP é:
$$ A(x) = 1500 – x(50 – 2x) $$
$$ A(x) = 1500 – 50x + 2x^2 $$
$$ A(x) = 2x^2 – 50x + 1500 $$
3) Calcular o valor de \(x\) que maximiza a área:
$$ x_v = -\frac{-50}{2 \cdot 2} = \frac{50}{4} = 12{,}5 $$
4) Verificando o valor da área máxima:
$$ A(12{,}5) = 2(12{,}5)^2 – 50 \cdot 12{,}5 + 1500 $$
$$ A = 2 \cdot 156,25 – 625 + 1500 = 312,5 – 625 + 1500 = 1187,5\ \text{cm}^2 $$
Mas a questão pede o valor de \(x\) que maximiza a área, não a área em si.
✅ Conclusão:
- Valor de \(x\) que maximiza a área de MNQP: $$ \boxed{12{,}5\ \text{cm}} $$
Questão 7. (Fuvest-SP) A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais.
Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?
a) R$ 2.000,00 b) R$ 3.200,00 c) R$ 3.600,00 d) R$ 4.000,00 e) R$ 4.800,00
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos uma relação entre preço e quantidade vendida. A arrecadação depende do produto entre a quantidade de combos vendidos e o preço de cada um.
1) Definir a variável:
Seja \( x \) o número de reais reduzidos no preço.
Então:
Preço: \( 10 – x \)
Quantidade: \( 200 + 100x \)
2) Função da arrecadação:
$$ R(x) = (10 – x)(200 + 100x) $$
Aplicando distributiva:
$$ R(x) = 10 \cdot 200 + 10 \cdot 100x – x \cdot 200 – x \cdot 100x $$
$$ R(x) = 2000 + 1000x – 200x – 100x^2 $$
$$ R(x) = -100x^2 + 800x + 2000 $$
3) Máximo da função:
$$ x_v = -\frac{b}{2a} = -\frac{800}{2 \cdot (-100)} = \frac{800}{200} = 4 $$
4) Substituir \( x = 4 \) na função:
Preço = R$ 6,00
Quantidade = \( 200 + 100 \cdot 4 = 600 \)
Arrecadação = \( 600 \cdot 6 = 3600 \)
✅ Conclusão:
- Máxima arrecadação: $$ \boxed{R\$ 3.600,00} $$
- Alternativa correta: c)
Questão 8. (UEG-GO) O lucro de uma empresa é dado pela relação \( R = L + C \), em que \( L \) é o lucro, \( R \) é a receita e \( C \) é o custo de produção.
Numa empresa que produziu \( x \) unidades de um produto, verificou-se que:
- \( C(x) = 2x^2 + 2500x + 3000 \)
- \( R(x) = x^2 + 7500x + 3000 \)
a) Esboce o gráfico da função \( L(x) \).
b) Quantas unidades essa empresa deve produzir para obter o maior lucro possível?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Sabemos que \( L(x) = R(x) – C(x) \), ou seja, lucro é a receita menos o custo. Devemos encontrar o valor de \( x \) que maximiza essa função \( L(x) \).
1) Subtrair as funções:
$$ L(x) = R(x) – C(x) $$
$$ L(x) = (x^2 + 7500x + 3000) – (2x^2 + 2500x + 3000) $$
$$ L(x) = x^2 – 2x^2 + 7500x – 2500x + 3000 – 3000 $$
$$ L(x) = -x^2 + 5000x $$
2) Encontrar o valor de \( x \) que maximiza \( L(x) \):
$$ x_v = -\frac{b}{2a} = -\frac{5000}{2 \cdot (-1)} = \frac{5000}{2} = 2500 $$
3) Lucro máximo:
$$ L(2500) = -2500^2 + 5000 \cdot 2500 $$
$$ L = -6\,250\,000 + 12\,500\,000 = 6\,250\,000 $$
✅ Conclusão:
- Quantidade para maior lucro: $$ \boxed{2500\ \text{unidades}} $$
- Lucro máximo: $$ \boxed{R\$ 6.250.000} $$
Questão 9. (UEA-AM) Em um plano cartesiano, a parábola descrita pela função quadrática:
$$ f(x) = x^2 – 4x + 3 $$
tem vértice no ponto \( V \), de abscissa 2, e passa pelo ponto \( P \), de abscissa 4.
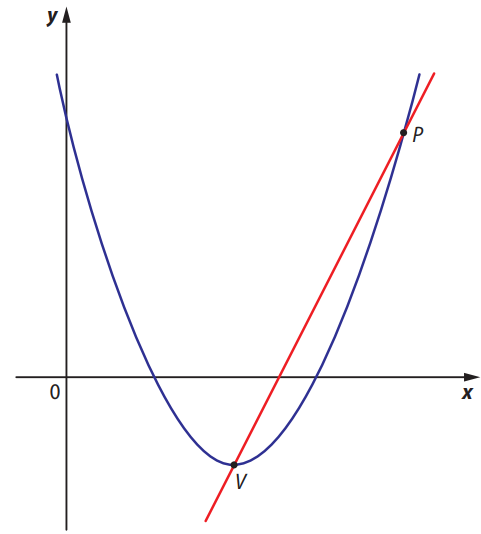
A reta que passa pelos pontos \( P \) e \( V \) intersecta o eixo \( y \) no ponto de ordenada igual a:
a) -2 b) -1 c) -4 d) -3 e) -5
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos encontrar a equação da reta que passa por dois pontos conhecidos da parábola: o vértice \( V = (2, f(2)) \) e o ponto \( P = (4, f(4)) \). Em seguida, determinamos o ponto onde essa reta cruza o eixo \( y \), ou seja, quando \( x = 0 \).
1) Calcular as coordenadas dos pontos:
$$ f(2) = 2^2 – 4 \cdot 2 + 3 = 4 – 8 + 3 = -1 \quad \Rightarrow V(2,\ -1) $$
$$ f(4) = 4^2 – 4 \cdot 4 + 3 = 16 – 16 + 3 = 3 \quad \Rightarrow P(4,\ 3) $$
2) Encontrar a equação da reta \( r \) que passa por \( V \) e \( P \):
Coeficiente angular:
$$ m = \frac{3 – (-1)}{4 – 2} = \frac{4}{2} = 2 $$
Equação da reta na forma reduzida:
$$ y – y_0 = m(x – x_0) $$
$$ y – (-1) = 2(x – 2) $$
$$ y + 1 = 2x – 4 $$
$$ y = 2x – 5 $$
3) Interseção com o eixo \( y \):
Para \( x = 0 \):
$$ y = 2 \cdot 0 – 5 = -5 $$
✅ Conclusão:
- Ordenada do ponto de interseção com o eixo \( y \): $$ \boxed{-5} $$
- Alternativa correta: e)