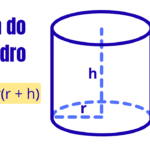
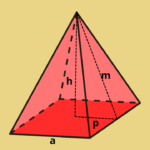
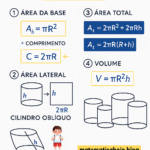
Fórmula de Euler para poliedros: como aplicar na prática?
A relação de Euler é uma das ideias mais elegantes da geometria espacial: conecta, em uma única equação, o número de vértices, arestas e faces de um poliedro. Com ela, você verifica rapidamente se um sólido é “bem comportado”, valida cálculos e descobre valores faltantes em provas. Neste guia direto, você verá quando a fórmula vale, exemplos resolvidos e exercícios com solução.
📘 Baixe grátis: eBook Fórmulas Matemática — resumo completo para consulta rápida.
Entenda a relação entre vértices, faces e arestas
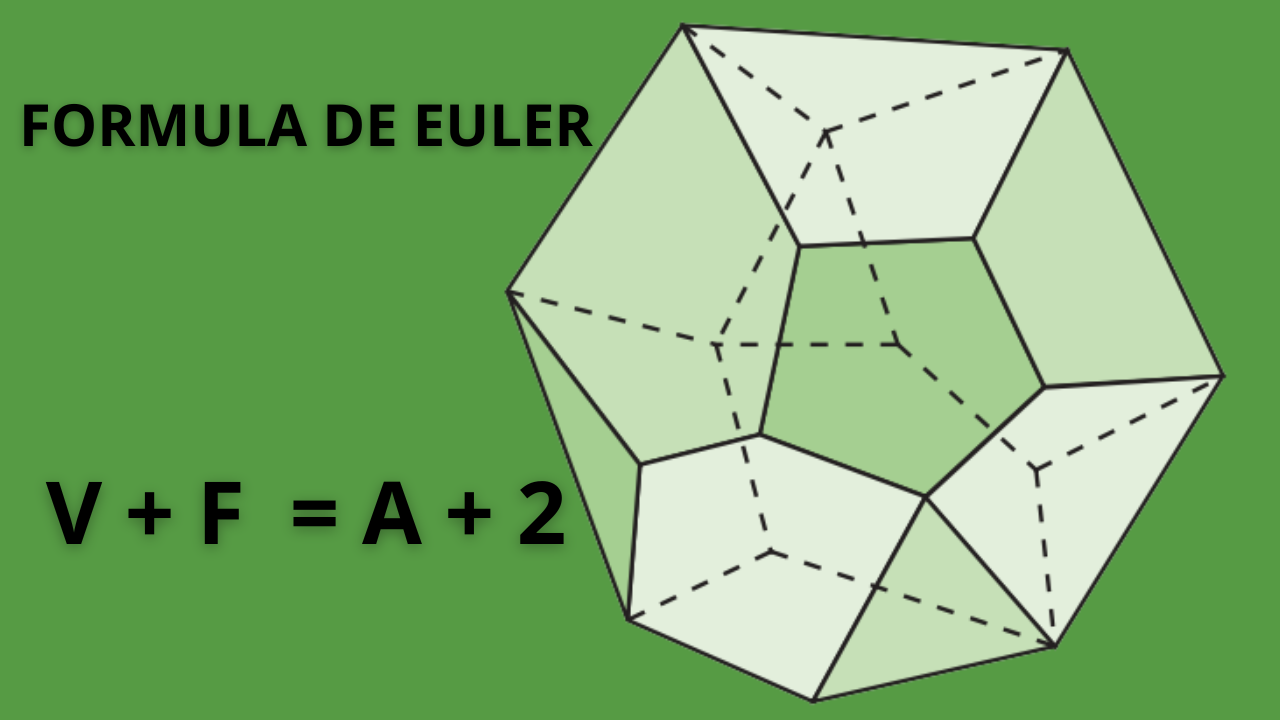
Para poliedros convexos, vale a identidade de Euler: . Aqui, é o número de vértices, é o número de arestas e é o número de faces. Em muitos enunciados, usa-se a forma equivalente: .
Quando a Fórmula de Euler é válida sem surpresas
A identidade funciona para poliedros convexos e conexos (prismas, pirâmides e sólidos platônicos). Em sólidos com “furos” (toroides) ou não convexos, a relação muda (topologia diferente).
Exemplo rápido: verificando um cubo
Para o cubo: , , . Então:
Critérios de uso e limitações da relação de Euler
Use a identidade apenas para poliedros com faces planas e sem desconexões. Cilindros e cones não são poliedros (superfícies curvas) e, portanto, não se enquadram.
Checklist prático antes de aplicar
- O sólido é convexo e tem apenas faces planas?
- Contou arestas “ocultas” no desenho?
- O sólido é uma única peça (conexo)?
Exemplos resolvidos passo a passo
1) Prisma pentagonal reto
Para um prisma de base pentagonal: , , .
2) Pirâmide quadrangular
Em uma pirâmide de base quadrada: , , .
3) Dodecaedro regular
No dodecaedro: , , .
🎯 Revisão visual: acelere o estudo com Mapas Mentais de Matemática.
Como usar a fórmula para achar valores faltantes
Exemplo prático de concurso
Uma caixa em forma de prisma triangular tem e . Quantas arestas possui?
📘 Download rápido: eBook de Fórmulas (Grátis) — leve a relação de Euler no bolso.
Exercícios com solução em abre/fecha
-
Exercício 1 – Prisma hexagonal
Um prisma reto de base hexagonal possui faces laterais retangulares. Determine , e . Verifique Euler.👀 Mostrar solução passo a passo
Base hexagonal ⇒ 6 vértices por base Arestas: 6 da base inferior + 6 da superior + 6 verticais Faces: 6 laterais + 2 bases Verificação -
Exercício 2 – Pirâmide pentagonal
Uma pirâmide regular de base pentagonal possui . Encontre e .👀 Mostrar solução passo a passo
Vértices: 5 da base + ápice Arestas: 5 da base + 5 laterais Verificação -
Exercício 3 – Octaedro
Um octaedro tem e . Determine .👀 Mostrar solução passo a passo
-
Exercício 4 – Validação de desenho
Um esboço mostra um sólido com , , . Pode ser convexo?👀 Mostrar solução passo a passo
Compatível com poliedro convexo (desde que todas as faces sejam planas). -
Exercício 5 – Descobrindo faces
Em um poliedro convexo, e . Calcule .👀 Mostrar solução passo a passo
Continue estudando: ENEM Matemática • Coleção 10 eBooks • Banco de Questões • eBook de Fórmulas (Grátis)
Conclusão
Ao ver um poliedro convexo, pense imediatamente em . Essa identidade agiliza conferências, evita erros de contagem e ajuda a determinar valores desconhecidos. Dominar esse “atalho” rende tempo e pontos em qualquer prova.
FAQ — Perguntas Frequentes
Quando posso aplicar a Fórmula de Euler sem exceções?
Em poliedros convexos e conexos (prismas, pirâmides e sólidos platônicos). Com furos ou partes desconexas, a característica topológica muda e a igualdade deixa de ser 2.
Cilindros e cones entram na relação de Euler?
Não. Eles têm superfícies curvas e não são poliedros. A identidade envolve sólidos de faces planas; por isso, não se aplica diretamente a cilindros e cones.
Por que o resultado de é 2?
Porque todo poliedro convexo é topologicamente equivalente a uma esfera. A característica de Euler dessa superfície é 2, e a identidade reflete esse fato.
Autor: Adriano Rocha — Matemática Hoje
Veja também: Mapas Mentais • Banco de Questões