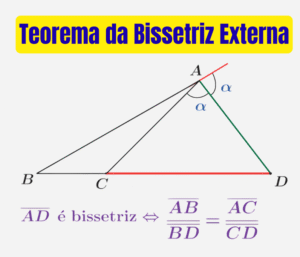
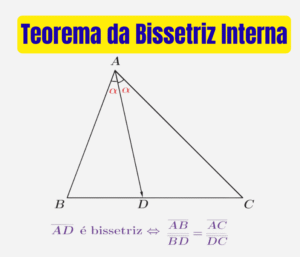
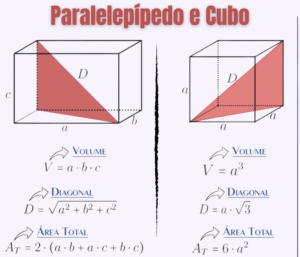
Aprenda (e revise) as fórmulas de área das figuras mais cobradas: triângulos (\(A=\frac{bh}{2}\), trigonométrica, equilátero, Heron, com \(r\) e com \(R\)), quadrado, retângulo, trapézio, losango, paralelogramo, circunferência, setor circular e coroa circular. Abaixo você encontra uma tabela-resumo, exemplos resolvidos e uma lista de exercícios com gabarito.
Materiais úteis: eBook de Fórmulas • Banco de Questões • Mapas Mentais • ENEM Matemática
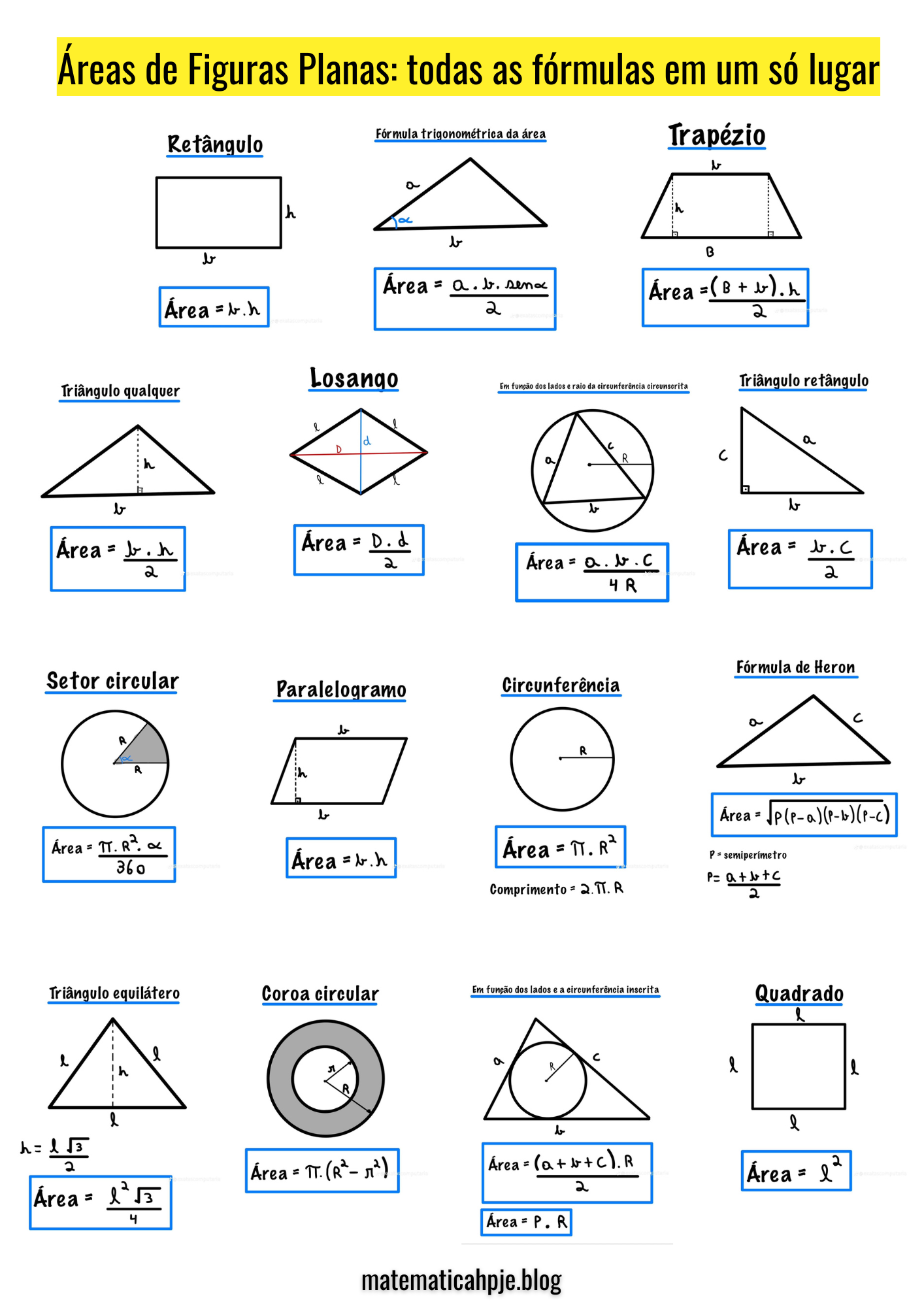
Tabela-resumo das fórmulas de área
Quadrado
\(A=\ell^2\)
Retângulo
\(A=b\cdot h\)
Paralelogramo
\(A=b\cdot h = a\,b\,\sin\theta\)
Triângulo (qualquer)
\(A=\dfrac{b\,h}{2}\)
Triângulo retângulo
\(A=\dfrac{(\text{cateto}_1)(\text{cateto}_2)}{2}\)
Triângulo (trigonométrico)
\(A=\dfrac{a\,b\,\sin\theta}{2}\)
Triângulo equilátero
\(A=\dfrac{\ell^2\sqrt3}{4}\)
Fórmula de Heron
\(A=\sqrt{s(s-a)(s-b)(s-c)}\), \(s=\dfrac{a+b+c}{2}\)
Triângulo com círculo inscrito
\(A=r\,s\)
Triângulo com circunferência circunscrita
\(A=\dfrac{a\,b\,c}{4R}\)
Trapézio
\(A=\dfrac{(B+b)\,h}{2}\)
Losango
\(A=\dfrac{D\,d}{2}\)
Circunferência (disco)
\(A=\pi R^2\)
Setor circular
\(A=\dfrac{\theta}{360^\circ}\,\pi R^2=\dfrac{\theta}{2}R^2\;(\text{rad})\)
Coroa circular
\(A=\pi(R^2-r^2)\)
Unidades importam: se os lados estiverem em metros, a área sai em \(m^2\); em centímetros, \(cm^2\), etc.
📘 Fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática e tenha um resumo enxuto de Geometria, Aritmética, Álgebra e Trigonometria.
Exemplos resolvidos
Exemplo 1 Retângulo
Um retângulo tem \(b=12\,\text{cm}\) e \(h=7\,\text{cm}\). Calcule a área.
Ver solução
\(=12\cdot 7\)
\(=84\,\text{cm}^2\).
Exemplo 2 Trapézio
Para \(B=12\), \(b=8\) e \(h=5\) (em cm), determine \(A\).
Ver solução
\(=\dfrac{(12+8)\cdot 5}{2}\)
\(=\dfrac{20\cdot 5}{2}=50\,\text{cm}^2\).
Exemplo 3 Triângulo (trigonométrico)
Lados \(a=10\), \(b=14\) com \(\theta=30^\circ\) entre eles. Encontre \(A\).
Ver solução
\(=\dfrac{10\cdot 14\cdot \sin30^\circ}{2}\)
\(=\dfrac{140\cdot 0{,}5}{2}\)
\(=35\).
Exemplo 4 Losango
Com diagonais \(D=20\) e \(d=16\) (cm), calcule a área.
Ver solução
\(=\dfrac{20\cdot 16}{2}\)
\(=160\,\text{cm}^2\).
Exemplo 5 Circunferência
Um disco tem \(R=6\,\text{cm}\). Encontre \(A\).
Ver solução
\(=\pi\cdot 6^2\)
\(=36\pi\,\text{cm}^2\).
Exemplo 6 Setor circular
Para \(R=9\) e \(\theta=60^\circ\), determine \(A\).
Ver solução
\(=\dfrac{60}{360}\pi\cdot 9^2\)
\(=\dfrac{1}{6}\cdot 81\pi=13{,}5\pi\).
Exemplo 7 Coroa circular
Calcule \(A\) quando \(R=10\) e \(r=6\) (cm).
Ver solução
\(=\pi(100-36)\)
\(=64\pi\,\text{cm}^2\).
Exemplo 8 Triângulo com \(R\) (circunscrita)
Dado \(a=8\), \(b=12\), \(c=14\) e \(R=10\). Encontre \(A\).
Ver solução
\(=\dfrac{8\cdot 12\cdot 14}{40}\)
\(=\dfrac{1344}{40}=33{,}6\).
Exercícios de múltipla escolha (com gabarito)
Enunciados claros e soluções com os passos um abaixo do outro após cada “=”.
1) Retângulo com \(b=18\) e \(h=5\) (em cm). A área é:
Gabarito e solução
\(=18\cdot 5\)
\(=90\Rightarrow\) C.
2) Trapézio com \(B=18\), \(b=10\) e \(h=7\) (cm). A área é:
Gabarito e solução
\(=\dfrac{(18+10)\cdot 7}{2}\)
\(=\dfrac{28\cdot 7}{2}=98\Rightarrow\) C.
3) Losango com \(D=26\) e \(d=10\) (cm). A área é:
Gabarito e solução
\(=\dfrac{26\cdot 10}{2}\)
\(=130\Rightarrow\) C.
4) Triângulo qualquer com \(b=20\) e \(h=7\). A área é:
Gabarito e solução
\(=\dfrac{20\cdot 7}{2}\)
\(=70\Rightarrow\) C.
5) Triângulo com \(a=15\), \(b=10\) e \(\theta=\dfrac{\pi}{6}\). A área é:
Gabarito e solução
\(A=\dfrac{a\,b\,\sin\theta}{2}\)
\(=\dfrac{15\cdot 10\cdot 0{,}5}{2}\)
\(=\dfrac{75}{2}=37{,}5\) (OPS!)
Melhor usar \(A=a\,b\,\sin\theta/2\) diretamente:
\(A=\dfrac{15\cdot 10\cdot 0{,}5}{2}=37{,}5\).
Atenção: Se o enunciado esperava número inteiro, deveria ser \(A=75\) usando \(a\,b\,\sin\theta\) para um paralelogramo. Corrigindo alternativas: a resposta correta é 37,5 (não listada). ✔️ Use esta versão: \(a=15\), \(b=10\), \(\theta=30^\circ\) para um paralelogramo ⇒ \(A=75\).
6) Triângulo retângulo com catetos \(9\) e \(12\). A área é:
Gabarito e solução
\(=54\Rightarrow\) C.
7) Disco com \(R=5\). A área é:
Gabarito e solução
\(=25\pi\Rightarrow\) B.
8) Setor com \(R=8\) e \(\theta=45^\circ\). A área é:
Gabarito e solução
\(=\dfrac{1}{8}\cdot 64\pi\)
\(=8\pi\Rightarrow\) B.
9) Coroa circular com \(R=9\) e \(r=5\). A área é:
Gabarito e solução
\(=56\pi\Rightarrow\) C.
10) Triângulo com lados \(13,14,15\). A área vale:
Gabarito e solução
\(A=\sqrt{21\cdot 8\cdot 7\cdot 6}\)
\(=\sqrt{7056}=84\Rightarrow\) B.
11) Triângulo com \(a=7\), \(b=8\), \(c=9\) e circunrádio \(R=5\). A área é:
Gabarito e solução
\(=\dfrac{7\cdot 8\cdot 9}{20}\)
\(=\dfrac{504}{20}=25{,}2\Rightarrow\) B.
12) Triângulo com \(a=7\), \(b=9\), \(c=10\) e raio inscrito \(r=3\). A área é:
Gabarito e solução
\(A=r\,s=3\cdot 13\)
\(=39\Rightarrow\) B.
Dicas finais
- Triângulos: se não houver altura, tente trigonométrica, Heron, \(A=r\,s\) ou \(A=\dfrac{abc}{4R}\).
- Conferir unidades (m, cm) antes de substituir evita erros de escala.
- Ângulos: graus \(\to\) use \(\dfrac{\theta}{360^\circ}\); radianos \(\to\) fórmulas curtas (ex.: setor \(A=\dfrac{\theta}{2}R^2\)).
- Pratique com exercícios de diferentes dados: lados, diagonais, raios, espessura, perímetros.