Frações aparecem em receitas, descontos, contas de água, provas de concursos e em praticamente toda a matemática básica. Neste guia, você vai entender o que são frações, como interpretar, simplificar, comparar e fazer operações com elas.
O que é uma fração?
De forma simples, fração é uma maneira de representar uma parte de um todo ou uma divisão entre números. Quando vemos algo como 3/4, estamos dizendo que temos 3 partes de um total dividido em 4 partes iguais.
Uma fração representa uma divisão. Se um bolo é cortado em 4 partes iguais e você pega 3 partes, você pegou a fração 3/4 do bolo.
Elementos de uma fração
Toda fração tem dois números:
- Numerador: o número de cima, indica quantas partes estão sendo consideradas.
- Denominador: o número de baixo, indica em quantas partes iguais o todo foi dividido.
Imagine uma pizza dividida em 8 fatias iguais. Se você come 3 fatias, pode dizer que comeu 3/8 da pizza (3 partes de um total de 8).
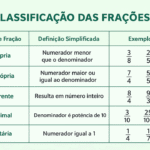
Tipos de frações
Classificar frações ajuda muito na interpretação dos exercícios e na resolução de provas.
1. Fração própria
É a fração em que o numerador é menor que o denominador. O valor da fração é menor que 1.
Exemplos: 1/2, 3/5, 7/8.
2. Fração imprópria
É a fração em que o numerador é maior ou igual ao denominador. O valor é maior ou igual a 1.
Exemplos: 5/3, 7/4, 9/9.
3. Fração aparente
É uma fração que, na prática, representa um número inteiro. Isso acontece quando o numerador é múltiplo do denominador.
Exemplos: 6/3 = 2, 10/5 = 2, 9/3 = 3.
4. Número misto
É a combinação de um número inteiro com uma fração própria.
Exemplo: 2 1/3 (lê-se: “dois inteiros e um terço”).
5. Frações equivalentes
Duas frações são equivalentes quando representam a mesma quantidade, mesmo com números diferentes.
1/2 e 2/4 são equivalentes, pois ambas representam “metade”. Se você multiplicar numerador e denominador de 1/2 por 2, obtém 2/4.
Regra prática: para gerar uma fração equivalente, você pode multiplicar ou dividir o numerador e o denominador pelo mesmo número diferente de zero.
Como simplificar uma fração
Simplificar uma fração é escrever a mesma fração com números menores, mas com o mesmo valor. A ideia é dividir numerador e denominador pelo mesmo número.
Se você dividir o numerador e o denominador pelo mesmo número natural (≠ 0), o valor da fração continua o mesmo.
Passo a passo para simplificar
- Procure um número que divida numerador e denominador ao mesmo tempo.
- Divida os dois por esse número.
- Repita o processo até não ser mais possível dividir por nenhum número inteiro além de 1.
12 e 18 são divisíveis por 2:
12 ÷ 2 = 6 e 18 ÷ 2 = 9 → 12/18 = 6/9
6 e 9 são divisíveis por 3:
6 ÷ 3 = 2 e 9 ÷ 3 = 3 → 6/9 = 2/3
Frações simplificada: 12/18 = 2/3.
Como comparar frações: maior, menor ou igual?
Em muitos exercícios, você precisa decidir qual fração é maior ou se duas frações são iguais. Existem algumas estratégias simples.
1. Quando os denominadores são iguais
Se os denominadores forem iguais, a fração com maior numerador é a maior.
Como o denominador é o mesmo (7), basta olhar o numerador: 5 > 3, logo 5/7 > 3/7.
2. Quando os denominadores são diferentes
Uma forma simples é transformar as frações para um denominador comum (MMC dos denominadores).
MMC(3, 4) = 12.
2/3 = (2×4)/(3×4) = 8/12.
3/4 = (3×3)/(4×3) = 9/12.
Conclusão: 9/12 > 8/12, logo 3/4 > 2/3.
Operações com frações
Agora que você já entende o que é uma fração, vamos ver como fazer as quatro operações principais: adição, subtração, multiplicação e divisão.
1. Soma e subtração com mesmo denominador
Quando os denominadores são iguais, somamos ou subtraímos apenas os numeradores.
Regra em palavras: (a/b) ± (c/b) = (a ± c)/b
Some os numeradores: 2 + 5 = 7.
Mantenha o denominador: 9.
Resultado: 2/9 + 5/9 = 7/9.
2. Soma e subtração com denominadores diferentes
Quando os denominadores são diferentes, precisamos igualá-los usando o MMC.
- Calcule o MMC dos denominadores.
- Transforme cada fração em uma fração equivalente com esse denominador comum.
- Some ou subtraia os numeradores e mantenha o denominador.
MMC(3, 4) = 12.
1/3 = 4/12 (multiplicamos por 4).
1/4 = 3/12 (multiplicamos por 3).
Somando: 4/12 + 3/12 = 7/12.
Resultado: 1/3 + 1/4 = 7/12.
3. Multiplicação de frações
Na multiplicação, basta multiplicar os numeradores entre si e os denominadores entre si.
Regra em palavras: (a/b) × (c/d) = (a×c)/(b×d)
Numeradores: 2 × 3 = 6.
Denominadores: 5 × 4 = 20.
Resultado inicial: 6/20.
Simplificando por 2: 6/20 = 3/10.
Resultado final: 2/5 × 3/4 = 3/10.
4. Divisão de frações
Dividir por uma fração é o mesmo que multiplicar pela fração inversa.
Regra em palavras: (a/b) ÷ (c/d) = (a/b) × (d/c)
Inverta a segunda fração: 2/5 → 5/2.
Faça a multiplicação: 3/4 × 5/2.
Numeradores: 3 × 5 = 15.
Denominadores: 4 × 2 = 8.
Resultado: 3/4 ÷ 2/5 = 15/8 (fração imprópria).
Frações, números decimais e porcentagens
Frações, decimais e porcentagens são três formas diferentes de representar a mesma ideia: uma parte de um todo.
1. Fração → decimal
Para transformar uma fração em decimal, basta realizar a divisão: numerador ÷ denominador.
| Fração | Divisão | Decimal |
|---|---|---|
| 1/2 | 1 ÷ 2 | 0,5 |
| 1/4 | 1 ÷ 4 | 0,25 |
| 3/5 | 3 ÷ 5 | 0,6 |
2. Fração → porcentagem
Para transformar uma fração em porcentagem, você pode:
- Transformar a fração em decimal e depois multiplicar por 100, ou
- Procurar uma fração equivalente com denominador 100.
3 ÷ 4 = 0,75.
0,75 × 100 = 75%.
Conclusão: 3/4 = 75%.
Erros comuns com frações (e como evitar)
- Somar denominadores na adição: por exemplo, achar que 1/2 + 1/3 = 2/5. Lembre-se: você deve usar o MMC para igualar os denominadores.
- Esquecer de simplificar: deixar respostas como 6/12 em vez de 1/2 pode atrapalhar na hora de comparar resultados.
- Errar na divisão de frações: ao invés de multiplicar pela inversa, muitos alunos tentam “dividir numerador com numerador e denominador com denominador”, o que está errado.
- Confundir fração própria com imprópria: lembrar que fração própria é menor que 1 e imprópria é maior ou igual a 1 ajuda na interpretação.
Exercícios resolvidos sobre frações
A melhor forma de aprender frações é praticando. Tente resolver primeiro e depois abra a solução.
Exercício 1: simplificação de fração
Simplifique a fração 45/60 até obter a forma irredutível.
Mostrar solução passo a passo
Passo 1: observe que 45 e 60 são múltiplos de 5.
45 ÷ 5 = 9 e 60 ÷ 5 = 12 → 45/60 = 9/12.
Passo 2: agora observe que 9 e 12 são múltiplos de 3.
9 ÷ 3 = 3 e 12 ÷ 3 = 4 → 9/12 = 3/4.
Resposta final: a fração simplificada é 3/4.
Exercício 2: soma de frações com denominadores diferentes
Calcule: 2/3 + 5/6.
Mostrar solução passo a passo
Passo 1: calcule o MMC dos denominadores (3 e 6).
MMC(3, 6) = 6.
Passo 2: transforme as frações para denominador 6.
2/3 = (2×2)/(3×2) = 4/6.
5/6 já está com denominador 6.
Passo 3: some as frações.
4/6 + 5/6 = 9/6.
Passo 4: simplifique 9/6.
9/6 = (dividindo por 3) → 3/2.
Resposta final: 2/3 + 5/6 = 3/2 (ou 1 1/2).
Exercício 3: frações e porcentagens
Em uma sala, 3/5 dos alunos são mulheres. Qual é a porcentagem de mulheres na sala?
Mostrar solução passo a passo
Passo 1: transforme a fração em decimal.
3 ÷ 5 = 0,6.
Passo 2: transforme o decimal em porcentagem.
0,6 × 100 = 60%.
Resposta final: as mulheres representam 60% dos alunos da sala.
Próximos passos para dominar frações e matemática básica
Se você quer continuar evoluindo em matemática, especialmente para provas, concursos e ENEM, recomendo aprofundar seus estudos com materiais organizados e focados.
Continue seus estudos com a Matemática Hoje
Veja alguns materiais que vão acelerar seu aprendizado:
Estudar frações com calma, revisando exemplos e praticando exercícios diariamente, transforma um conteúdo que parece “difícil” em algo natural. Volte a este guia sempre que tiver dúvidas e use os recursos recomendados para fortalecer sua base em matemática.