(CESPE / CEBRASPE 2024 – Prefeitura de Joinville – SC – Professor de Matemática)

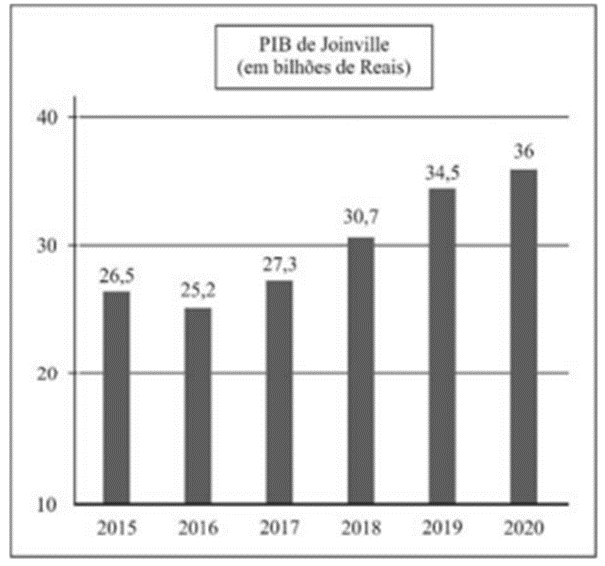
O gráfico a seguir apresenta a evolução do PIB da cidade de Joinville no período de 2015 a 2020.

Considere que o valor do PIB de Joinville ao longo dos anos seja estimado, em bilhões de reais, por uma função linear P(t), em que t = 10 representa o ano de 2010, t = 11, o ano de 2011 e assim sucessivamente. Nesse caso, se P(15) = 26,5 e P(19) = 34,5, então, para o ano de 2020, a diferença, em bilhões de reais, entre o valor estimado pela função P(t) e o valor dado no gráfico é

A) inferior a 0,31.

B) superior a 0,31 e inferior a 0,39.

C) superior a 0,39 e inferior a 0,47.

D) superior a 0,47 e inferior a 0,55.

E) superior a 0,55.

Solução em vídeo

Para resolver a questão, precisamos primeiro determinar a Função Afim (Função do 1° Grau) P(t) que representa o PIB de Joinville ao longo dos anos. Sabemos que:

• P(15)=26,5 bilhões de reais (em 2015).
• P(19)=34,5 bilhões de reais (em 2019).

Passo 1: Encontrar a equação da reta P(t)=at+b

Podemos usar os dois pontos dados para encontrar a inclinação a da reta:

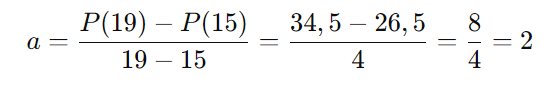
Agora, usando um dos pontos para encontrar b:

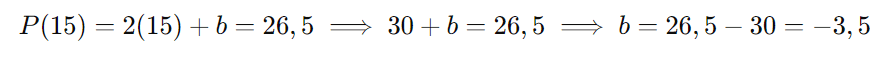
Assim, a função é:

P(t)=2t−3,5

Passo 2: Calcular o PIB estimado para 2020 (t=20)

P(20)=2(20)−3,5=40−3,5=36,5 bilhões de reais

Passo 3: Comparar o valor estimado com o valor dado no gráfico

Vamos supor que o gráfico forneça um valor diferente para o PIB em 2020. A diferença será:

Diferença = P(20)− 36∣ = 36,5− 36 = 0,5

Alternativa correta Letra D