Em matemática, as funções podem ser classificadas como pares ou ímpares dependendo de como elas se comportam em relação à simetria no plano cartesiano.
📌 Função Par
Uma função f(x) é chamada de par se satisfaz a seguinte condição para todo x no domínio da função: f(-x) = f(x)
Essa propriedade indica que a função é simétrica em relação ao eixo y. Ou seja, se um ponto (x, y) pertence ao gráfico da função, então o ponto (-x, y) também pertence.
🔹 Exemplos de funções pares:
- f(x) = x2, pois (−x)2 = x2.
- f(x)=cosx, pois cos(−x) = cosx.
- f(x) = x4 + 2x2 + 1, pois todos os expoentes de x são pares.
📌 Gráfico de uma função par: O gráfico é sempre simétrico em relação ao eixo y.
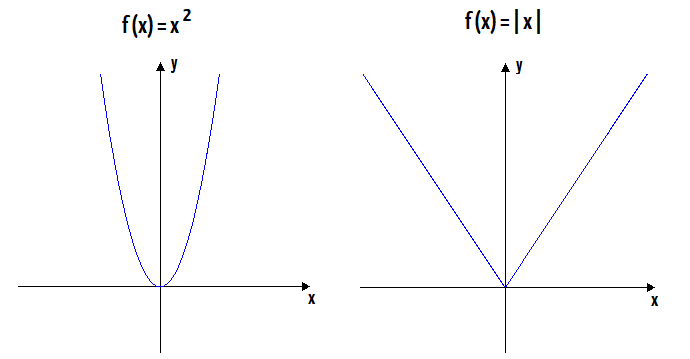
Exemplo
A função representada no gráfico abaixo e par é aquela que tem simetria em relação ao eixo y. Ou seja, para qualquer valor de x no domínio da função, a função de −x é igual à função de x, ou seja,
f(-x) = f(x).
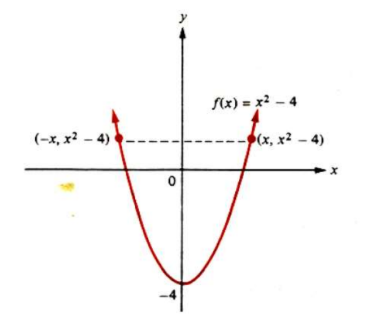
No gráfico apresentado , temos uma função quadrática f(x) = x2 − 4. Como podemos ver, a função é simétrica em relação ao eixo y, o que caracteriza uma função par.
Exemplo
Vamos testar a função par dada: f(x) = x2 − 4
Lembre-se que, para ser par, a função deve satisfazer f(−x) = f(x)
Para x = 2 e x = -2
- f(2) = 22 − 4 = 4 − 4 = 0
- f(−2) = (−2)2 − 4 = 4 − 4 = 0
✅ Como f(2) = f(−2), a função é par para esse valor.
Para x = 3 e x = -3
- f(3) = 32 − 4 = 9 − 4 = 5
- f(−3) = (−3)2 − 4 = 9 − 4 = 5
✅ Como f(3) = f(−3), a função mantém a simetria.
Para x=4 e x = -4
- f(4) = 42 − 4 = 16 − 4 = 12
- f(−4)=(−4)2 − 4 = 16 − 4 = 12
✅ Como f(4)=f(−4)f(4) = f(-4)f(4)=f(−4), a função continua sendo par.
📌 Função Ímpar
Uma função f(x) é chamada de ímpar se satisfaz a seguinte condição para todo x no domínio da função:
f(−x) = −f(x)
Isso significa que o gráfico da função possui simetria em relação à origem. Ou seja, se o ponto (x, y) pertence ao gráfico da função, então o ponto (-x, -y) também pertence.
🔹 Exemplos de funções ímpares:
- f(x) = x3, pois (−x)3 = −x3
- f(x)=senx, pois sen(−x) = −senx
- f(x) = x5 − x, pois todos os expoentes de x são ímpares.
📌 Gráfico de uma função ímpar: O gráfico é simétrico em relação à origem.
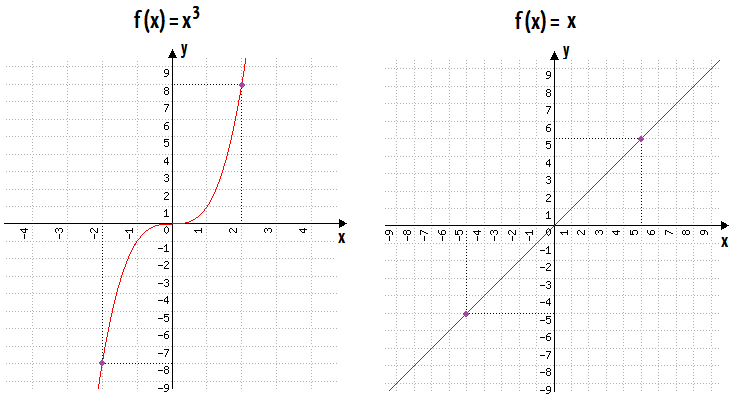
Já a função representada no gráfico abaixo é ímpar e tem simetria em relação à origem. Isso significa que para todo x, a função de −x é o oposto da função de x, ou seja, f(-x) = -f(x).
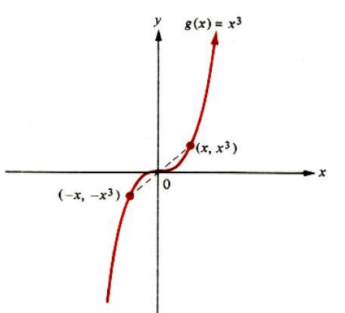
No gráfico , temos a função cúbica g(x) = x3. Essa função é simétrica em relação à origem, pois, ao inverter o sinal de x, o sinal de g(x) também inverte. Isso caracteriza a função como ímpar.
gora vamos testar a função ímpar dada no gráfico: g(x) = x3
Uma função é ímpar se satisfaz a condição:
g(−x) = −g(x)
Ou seja, trocar x por −x deve resultar no oposto de g(x).
Para x = 2 e x = -2
- g(2) = 23 = 8
- g(−2) = (−2)3 = −8
✅ Como g(-2) = -g(2), a função mantém a simetria ímpar.
Para x = 3 e x = -3
- g(3) = 33 = 27
- g(−3) = (−3)3 = −27
✅ Como g(-3) = -g(3), a função continua sendo ímpar.
Para x = 4 e x = -4
- g(4) = 43 = 64
- g(−4) = (−4)3 = −64
✅ Como g(-4) = -g(4), a função confirma sua propriedade ímpar.
Lista de Exercício Função Par e Ímpar
Exercício 1
Considere a função f(x) = x4 − 2x2 + 1. Verifique se ela é uma função par.
Ver Solução
Resolução
Para ser par, a função deve satisfazer: f(−x) = f(x)
Calculamos f(−x):
f(−x) = (−x)4 − 2(−x)2 + 1 = x4 − 2x2 + 1
Como f(−x) = f(x), a função é par.
Exercício 2:
Verifique se a função g(x) = x5 − x é ímpar.
Ver Solução
Resolução
Para ser ímpar, a função deve satisfazer: g(−x) = −g(x)
Calculamos g(−x):
g(−x) = (−x)5−(−x) = −x5 + x
Agora, calculamos −g(x):
−g(x) = −(x5 − x) = −x5 + x
Como g(−x) = −g(x), a função é ímpar.
Exercício 3:
A função h(x) = x3 + x2 é par, ímpar ou nenhuma das duas?
Ver Solução
Resolução
Verificamos se a função é par:
h(−x) = (−x)3 + (−x)2 = −x3 + x2
Como h(−x) ≠ h(x), a função não é par.
Agora, verificamos se a função é ímpar:
−h(x) = −(x3 + x2) = −x3 − x2
Como h(−x) ≠ −h(x), a função não é ímpar.
Resposta: A função não é nem par nem ímpar.
