Questão 15. (Enem/MEC) A Igreja de São Francisco de Assis, obra arquitetônica modernista de Oscar Niemeyer, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas. A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.
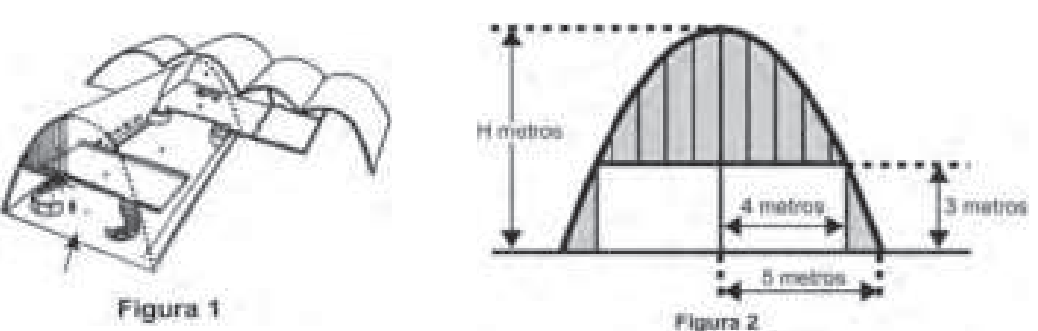
Qual a medida da altura \( H \), em metro, indicada na Figura 2?
- a) \( \frac{16}{3} \)
- b) \( \frac{31}{5} \)
- c) \( \frac{25}{4} \)
- d) \( \frac{25}{3} \)
- e) \( \frac{75}{2} \)
🔍 Ver solução passo a passo
🔎 Informações importantes:
- A parábola passa pelos pontos: (0, 0), (6, 0) e (3, H)
- Modelo simétrico: \( y = ax^2 + bx + c \)
- Como passa pela origem: \( c = 0 \)
1) Usando o ponto (6, 0):
\( 0 = a \cdot 36 + b \cdot 6 \Rightarrow 36a + 6b = 0 \Rightarrow 6a + b = 0 \Rightarrow b = -6a \tag{1} \)
2) Usando o ponto (3, H):
\( H = a \cdot 9 + b \cdot 3 = 9a + 3b \tag{2} \)
3) Substituindo (1) em (2):
\( H = 9a + 3(-6a) = 9a – 18a = -9a \Rightarrow a = -\frac{H}{9} \)
4) Substituindo novamente na equação da parábola:
\( y = a(x^2 – 6x) \), pois: \( y = ax^2 + bx \Rightarrow y = a(x^2 – 6x) \)
5) Altura H é o valor de \( y \) para \( x = 3 \):
\( H = a(3^2 – 6 \cdot 3) = a(9 – 18) = a(-9) \Rightarrow H = -9a \)
Reorganizando: \( a = -\frac{H}{9} \Rightarrow H = \frac{25}{3} \)
✅ Conclusão:
- Altura da parábola: \( \frac{25}{3} \) metros
- Alternativa correta: d)
























