Questão 5. (UFJF-MG) Sobre os lados do retângulo \(ABCD\), de dimensões 30 cm e 50 cm, marcam-se os pontos \(M\), \(N\), \(P\) e \(Q\) de forma que a distância dos pontos \(M\) e \(N\) ao vértice \(A\) e dos pontos \(P\) e \(Q\) ao vértice \(C\) sejam iguais a \(x\) centímetros. Veja a figura:
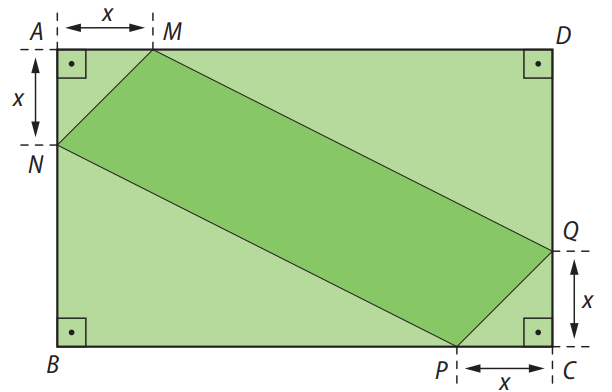
Determine o valor de \(x\) de modo que o quadrilátero \(MNQP\) tenha área máxima.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Os pontos \(M\), \(N\), \(P\) e \(Q\) são marcados a uma distância \(x\) das extremidades dos vértices do retângulo. Desejamos determinar a área máxima da região em verde (quadrilátero \(MNQP\)), que pode ser obtida pela subtração da área de dois triângulos dos cantos da área total do retângulo.
1) Área do retângulo total:
$$ A_{\text{total}} = 30 \cdot 50 = 1500\ \text{cm}^2 $$
2) Área da região MNQP:
A região MNQP é o retângulo menos dois triângulos idênticos formados nos cantos com catetos \(x\) e \(50 – 2x\).
Área de um triângulo:
$$ A_{\text{triângulo}} = \frac{x(50 – 2x)}{2} $$
Área total dos dois triângulos:
$$ A_{\text{triângulos}} = 2 \cdot \frac{x(50 – 2x)}{2} = x(50 – 2x) $$
Logo, a área do quadrilátero MNQP é:
$$ A(x) = 1500 – x(50 – 2x) $$
$$ A(x) = 1500 – 50x + 2x^2 $$
$$ A(x) = 2x^2 – 50x + 1500 $$
3) Calcular o valor de \(x\) que maximiza a área:
$$ x_v = -\frac{-50}{2 \cdot 2} = \frac{50}{4} = 12{,}5 $$
4) Verificando o valor da área máxima:
$$ A(12{,}5) = 2(12{,}5)^2 – 50 \cdot 12{,}5 + 1500 $$
$$ A = 2 \cdot 156,25 – 625 + 1500 = 312,5 – 625 + 1500 = 1187,5\ \text{cm}^2 $$
Mas a questão pede o valor de \(x\) que maximiza a área, não a área em si.
✅ Conclusão:
- Valor de \(x\) que maximiza a área de MNQP: $$ \boxed{12{,}5\ \text{cm}} $$






















