Questão 4. Murilo comprou 40 metros de cerca para fazer um cercado em formato de retângulo para seu cachorro no quintal de sua moradia. Ele vai aproveitar uma parede como um dos lados do cercado, de acordo com a figura a seguir:
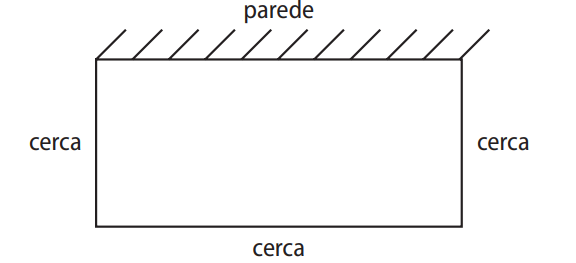
Sabendo que ele vai utilizar toda a cerca comprada, qual é a área máxima que esse cercado poderá ter?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos um retângulo com um lado encostado na parede, ou seja, ele usará a cerca apenas em 3 lados: 2 lados menores (largura) e 1 lado maior (comprimento).
Seja \( x \) a largura do cercado e \( y \) o comprimento (paralelo à parede).
1) Relacionar o perímetro com a cerca disponível:
$$ 2x + y = 40 \Rightarrow y = 40 – 2x $$
2) Escrever a função da área:
$$ A(x) = x \cdot y = x(40 – 2x) $$
$$ A(x) = 40x – 2x^2 $$
3) Encontrar o valor de \( x \) que fornece a área máxima:
$$ x_v = -\frac{b}{2a} = -\frac{40}{2 \cdot (-2)} = \frac{40}{4} = 10 $$
4) Calcular a área máxima:
$$ y = 40 – 2 \cdot 10 = 20 $$
$$ A = 10 \cdot 20 = 200\ m^2 $$
✅ Conclusão:
- Área máxima do cercado: $$ 200\ m^2 $$






















