A função racional é um dos tipos mais importantes de funções matemáticas, pois descreve relações entre variáveis por meio de frações algébricas. Essas funções aparecem frequentemente em problemas de física, economia, engenharia e nas provas de concursos.
O que é uma Função Racional?
Chamamos de função racional toda função que pode ser escrita na forma:
f(x) = p(x) / q(x)
Onde:
- p(x) e q(x) são funções polinomiais;
- q(x) ≠ 0, ou seja, o denominador não pode ser zero.
Exemplos de funções racionais:
- f(x) = (2x + 1)/(x – 3)
- f(x) = (x² – 4)/(x + 2)
- f(x) = 1/x
Domínio da Função Racional
O domínio de uma função racional é o conjunto de todos os números reais x para os quais o denominador q(x) não é zero.
Exemplo:
Considere f(x) = (x + 1)/(x – 2)
Nesse caso, o denominador x – 2 ≠ 0 → x ≠ 2
Portanto, o domínio é todos os reais, exceto x = 2.
Gráfico da Função Racional
As funções racionais geralmente possuem comportamentos específicos, como:
- Assíntotas verticais nos valores que anulam o denominador.
- Assíntotas horizontais ou oblíquas dependendo do grau dos polinômios.
Essas características ajudam a esboçar o gráfico da função racional e compreender o seu comportamento.
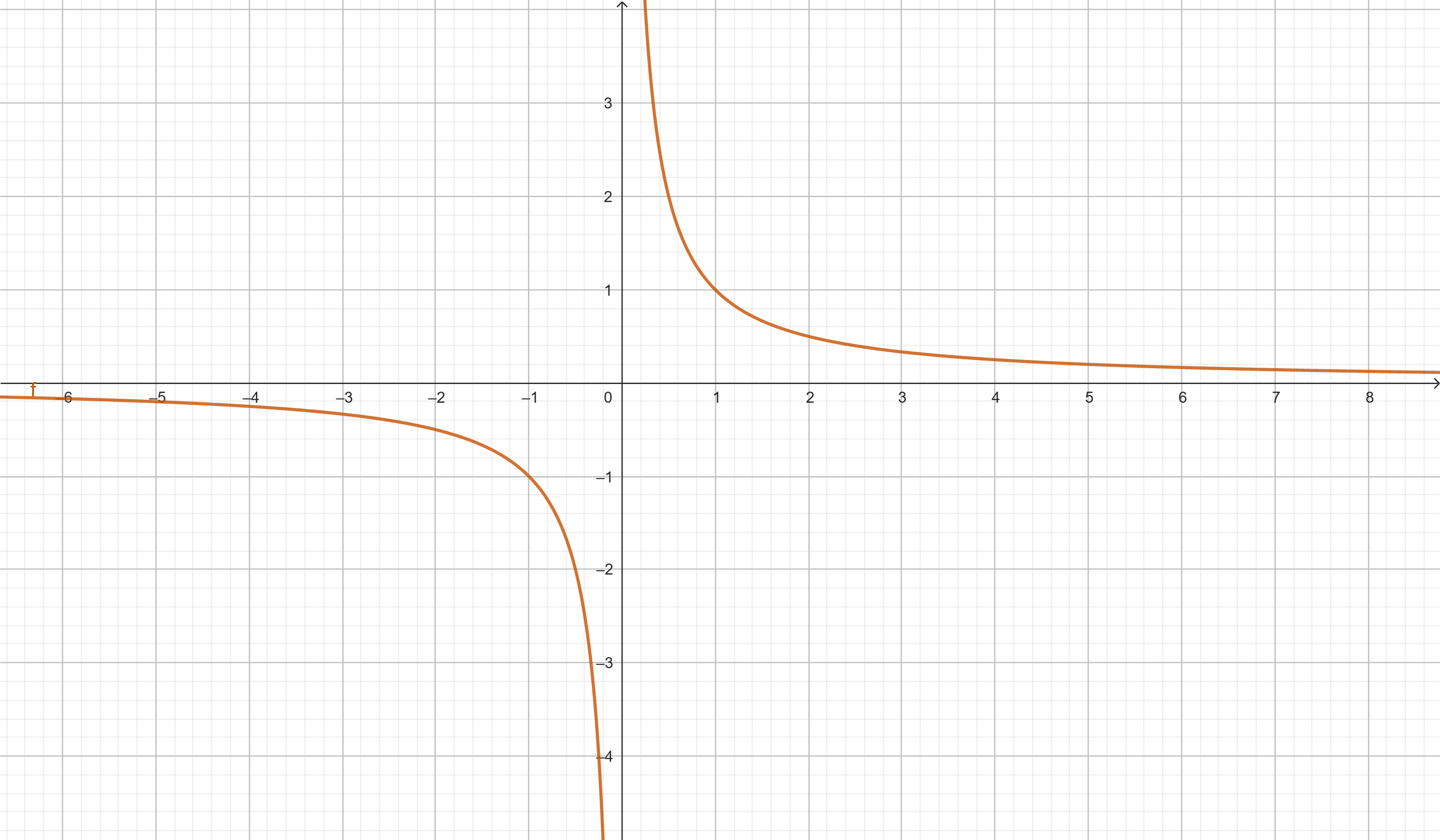
Exemplo de gráfico:
f(x) = 1/x possui assíntota vertical em x = 0 e assíntota horizontal em y = 0.
Exercícios Resolvidos
Exercício 1
Determine o domínio da função f(x) = (x² + 3x)/(x² – 9)
Solução:
O denominador é x² – 9 = (x – 3)(x + 3). Logo, x ≠ 3 e x ≠ -3.
Domínio: todos os reais, exceto -3 e 3.
Exercício 2
Simplifique a função f(x) = (x² – 1)/(x – 1)
Solução:
Numerador: x² – 1 = (x – 1)(x + 1)
f(x) = [(x – 1)(x + 1)] / (x – 1) → simplifica para f(x) = x + 1, com restrição x ≠ 1
Exercício 3
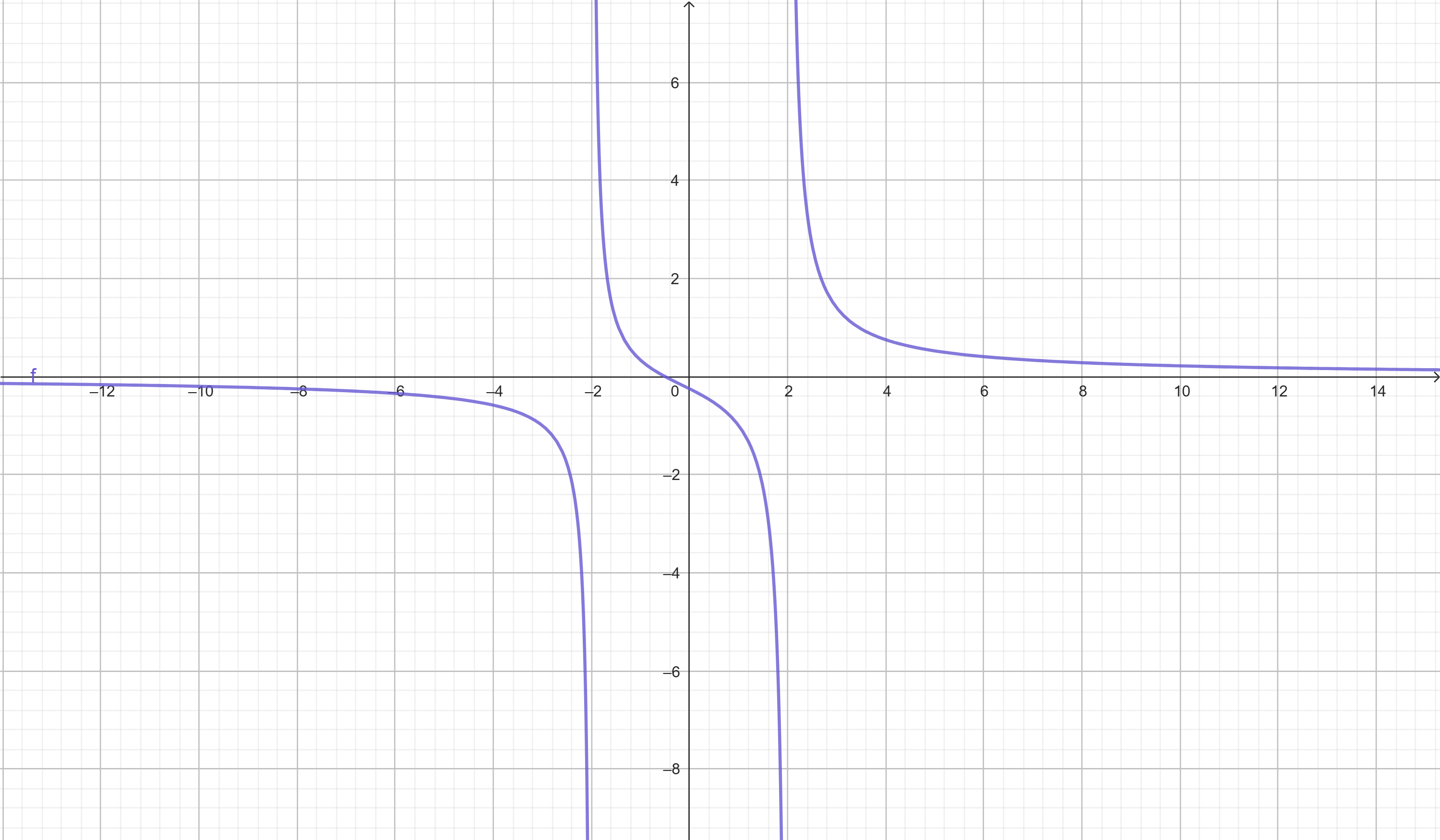
Encontre as assíntotas verticais da função f(x) = (2x + 1)/(x² – 4)
Solução:
Denominador: x² – 4 = (x – 2)(x + 2)
Assíntotas verticais em x = 2 e x = -2
Exercício 4
Para a função f(x) = (x² + 2x + 1)/(x + 1), simplifique a expressão.
Solução:
Numerador: x² + 2x + 1 = (x + 1)²
f(x) = [(x + 1)²] / (x + 1) = x + 1, com restrição x ≠ -1
Exercício 5
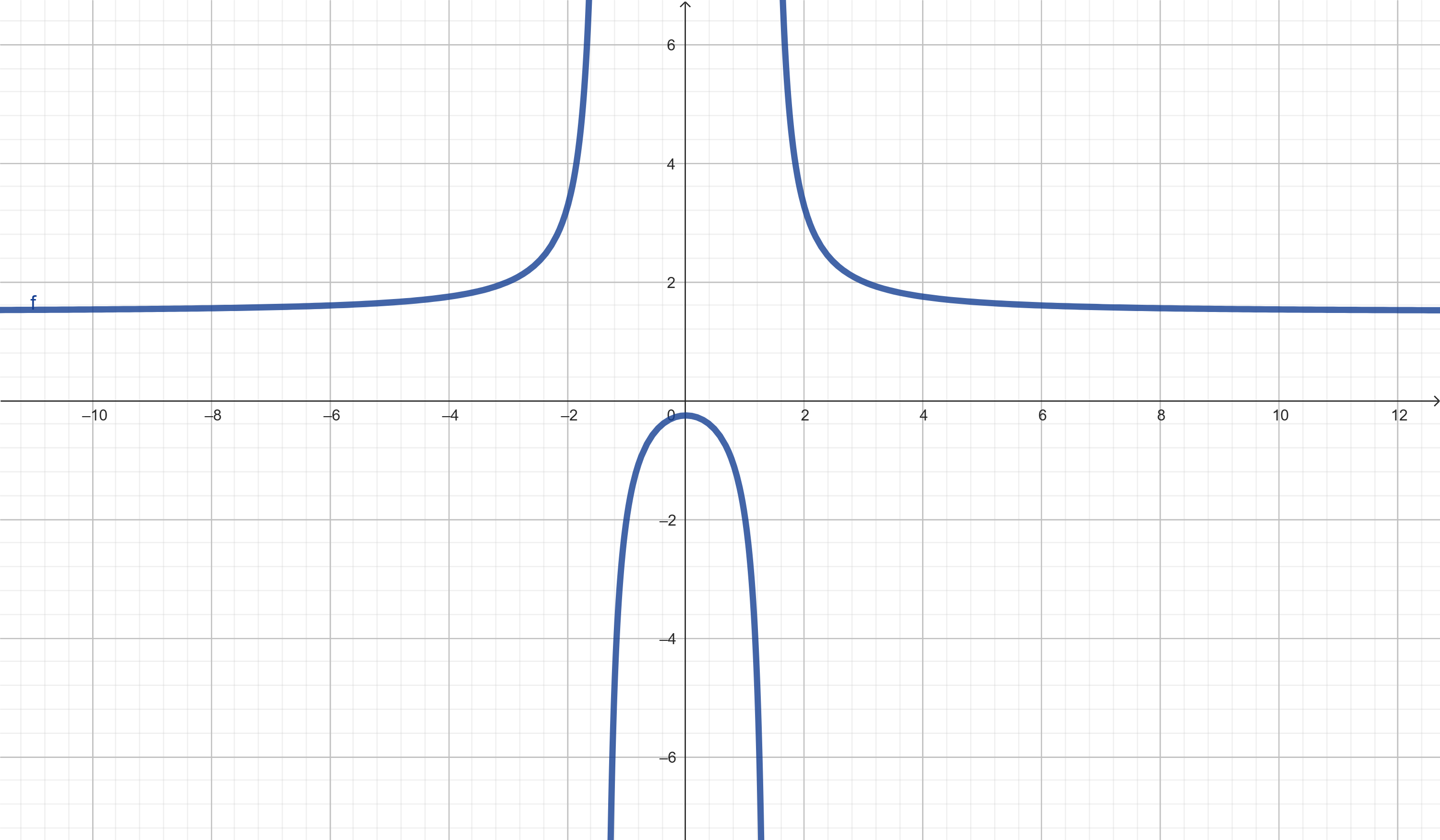
Verifique se há assíntota horizontal em f(x) = (3x² + 1)/(2x² – 4)
Solução:
2x² – 4 = 0
x² = 2
x = ±√2
y = 3/2 → assíntota horizontal em y = 3/2
Conclusão
A função racional é uma ferramenta poderosa da matemática que ajuda a entender diversas situações em que uma variável depende da razão entre dois polinômios. Seu estudo envolve o domínio, assíntotas, simplificações e o comportamento gráfico.
Continue praticando e, se quiser aprofundar ainda mais seus estudos, veja nossos outros artigos sobre funções e gráficos matemáticos!
























