A Geometria Analítica é uma área da matemática que une conceitos algébricos e geométricos, permitindo resolver problemas geométricos utilizando coordenadas e equações. Um dos conceitos fundamentais dessa disciplina é o ponto, que representa uma posição no espaço. Neste artigo, abordaremos as definições e cálculos relacionados aos pontos, especialmente os pontos A e B, a distância entre eles, o ponto médio e a colinearidade.
1. Coordenadas de um Ponto
Um ponto no plano cartesiano é definido por suas coordenadas (x, y), que indicam sua posição em relação aos eixos x e y. O ponto A(xA, yA) tem como coordenadas xA e yA, enquanto o ponto B(xB, yB) é definido por xB e yB.
2. Distância entre Dois Pontos
A distância entre dois pontos A(xA, yA) e B(xB, yB) no plano cartesiano pode ser calculada utilizando a fórmula da distância, que é derivada do Teorema de Pitágoras. A fórmula é dada por:

Essa fórmula calcula a distância direta entre os pontos A e B como se estivéssemos traçando uma linha reta entre eles.
Exemplo Prático:
Se A(2, 3) e B(5, 7), a distância d(A, B) é calculada assim:
d(A, B)2 = (5 – 2)2 + (7 – 3)2 = 32 + 42 = 9 + 16 = 25 ⇒ d(A, B)2 = 25 ⇒ d(A, B)= √25 ⇒ d(A, B)= 5
3. Ponto Médio
O ponto médio ( M ) de um segmento de reta que conecta dois pontos A(xA, yA) e B(xB, yB) é o ponto que divide o segmento em duas partes iguais. As coordenadas do ponto médio são calculadas pela média aritmética das coordenadas dos pontos A e B:
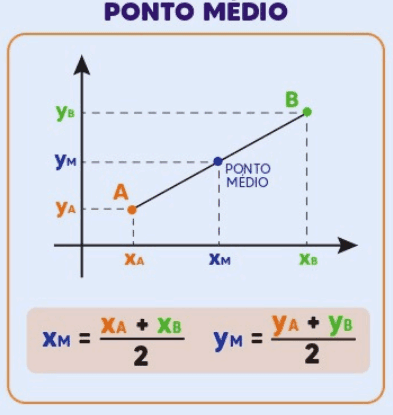
Exemplo Prático:
Para A(2, 3) e B(5, 7), o ponto médio M é:
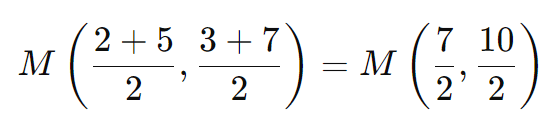
4. Pontos Colineares
Três ou mais pontos são ditos colineares se estiverem alinhados em uma mesma reta. Para determinar se os pontos A(xA, yA), B(xB, yB) e C(xC, yC) são colineares, é necessário verificar se a área do triângulo formado por esses três pontos é igual a zero.
A área de um triângulo formado por três pontos no plano pode ser calculada usando a seguinte fórmula:
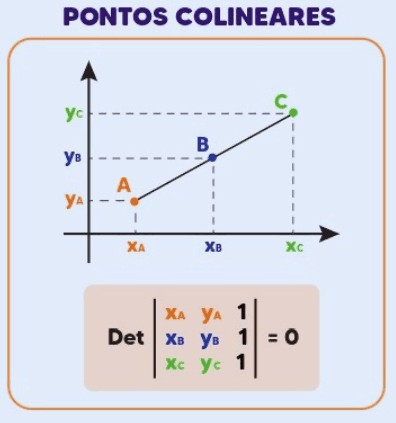
Se a área for igual a zero, os pontos são colineares, ou seja, estão sobre a mesma reta.
Exemplo Prático:
Para os pontos A(1, 2), B(3, 6) e C(5, 10), a área é calculada assim:
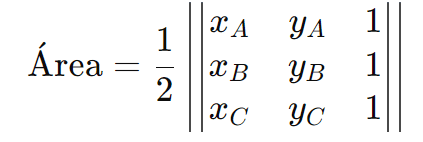
Substituindo as coordenadas dos pontos A, B, e C:
Agora, vamos calcular o determinante dessa matriz 3×3

Portanto, a área é igual a zero, o que confirma que os pontos A, B e C são colineares.
Conclusão
O estudo dos pontos em Geometria Analítica é essencial para compreender a relação entre diferentes figuras geométricas no plano. Através das coordenadas de um ponto, podemos calcular a distância entre dois pontos, encontrar o ponto médio de um segmento e verificar se três ou mais pontos são colineares. Esses conceitos são fundamentais e amplamente utilizados em diversas aplicações matemáticas e científicas.
Leia também
Geometria Analítica: Pontos ⇒ Distância, Ponto Médio e Colinearidade
Distância entre Retas e Cálculo da Área de um Triângulo
Circunferência: Equação Geral e Reduzida
A Parábola: Definição, Propriedades e Equações

























