Conteúdo: Leitura e interpretação de gráficos de funções
Questão 17. (UFV-MG) O gráfico a seguir ilustra a evolução da temperatura \( T \) (°C), em uma região, ao longo de um período de 24 horas.
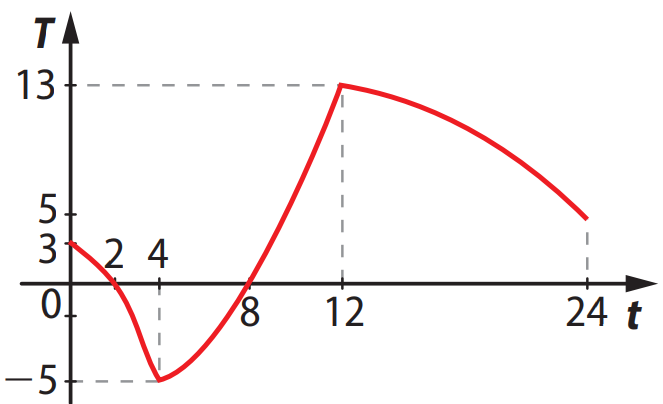 Determine:
a) os horários em que a temperatura atinge
0 °C; às 2 h e às 8 h
b) o intervalo de variação da temperatura ao
longo das 24 horas;
c) os intervalos de tempo em que a temperatura é positiva.
Determine:
a) os horários em que a temperatura atinge
0 °C; às 2 h e às 8 h
b) o intervalo de variação da temperatura ao
longo das 24 horas;
c) os intervalos de tempo em que a temperatura é positiva.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Precisamos analisar o gráfico da função \( T(t) \), que representa a temperatura ao longo do tempo em horas, para determinar:
- Quando \( T(t) = 0^\circ \text{C} \);
- O intervalo de variação da temperatura;
- Os intervalos em que \( T(t) > 0 \).
a) Horários em que a temperatura é 0 ºC:
Observando o gráfico, a temperatura cruza o eixo \( x \) nos pontos:
$$ t = 2\text{h} \quad \text{e} \quad t = 8\text{h} $$
b) Intervalo de variação da temperatura:
O valor mínimo é \( -5^\circ \text{C} \) e o máximo é \( 13^\circ \text{C} \).
$$ \text{Variação: } [-5,\ 13] $$
c) Intervalo de tempo com temperatura positiva:
A função é positiva quando está acima do eixo \( x \), ou seja:
$$ t \in (0,\ 2) \cup (8,\ 24) $$
✅ Conclusão:
- a) Temperatura igual a 0 °C: às 2h e às 8h
- b) Intervalo de variação: de −5 °C a 13 °C
- c) Intervalos com temperatura positiva: de 0h às 2h e de 8h às 24h






















