📝 Questão 1
Conteúdo: Funções afins – construção e interpretação gráfica
Construa, no sistema cartesiano ortogonal, o gráfico das seguintes funções:
- a) \( f(x) = 2x + 1 \)
- b) \( g(x) = -x + 4 \)
- c) \( y = \dfrac{1}{2} – x \)
- d) \( h(x) = -2x \)
🔍 Ver solução passo a passo
Função a) \( f(x) = 2x + 1 \)
- Coeficiente angular: \( a = 2 \) (reta crescente)
- Ponto 1: \( x = 0 \Rightarrow f(0) = 1 \) → \( (0, 1) \)
- Ponto 2: \( x = 1 \Rightarrow f(1) = 3 \) → \( (1, 3) \)
✅ Trace a reta passando por (0, 1) e (1, 3)
a)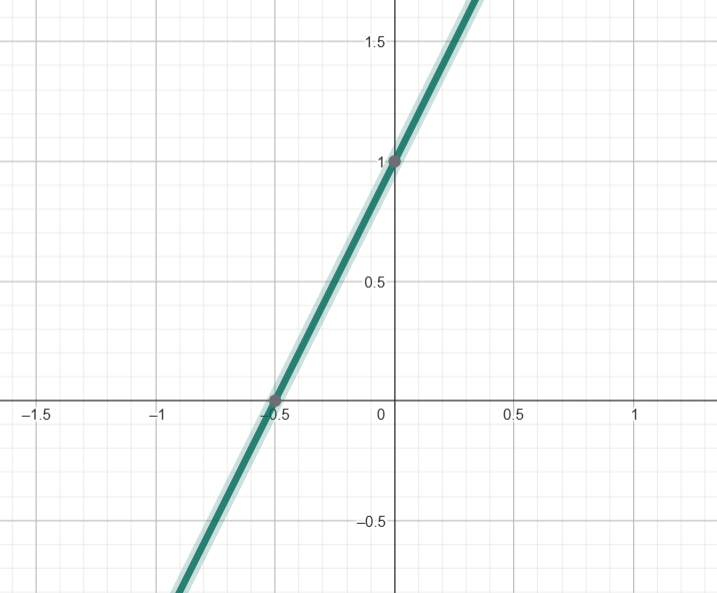
Função b) \( g(x) = -x + 4 \)
- Coeficiente angular: \( a = -1 \) (reta decrescente)
- Ponto 1: \( x = 0 \Rightarrow g(0) = 4 \) → \( (0, 4) \)
- Ponto 2: \( x = 2 \Rightarrow g(2) = 2 \) → \( (2, 2) \)
✅ Trace a reta passando por (0, 4) e (2, 2)
b)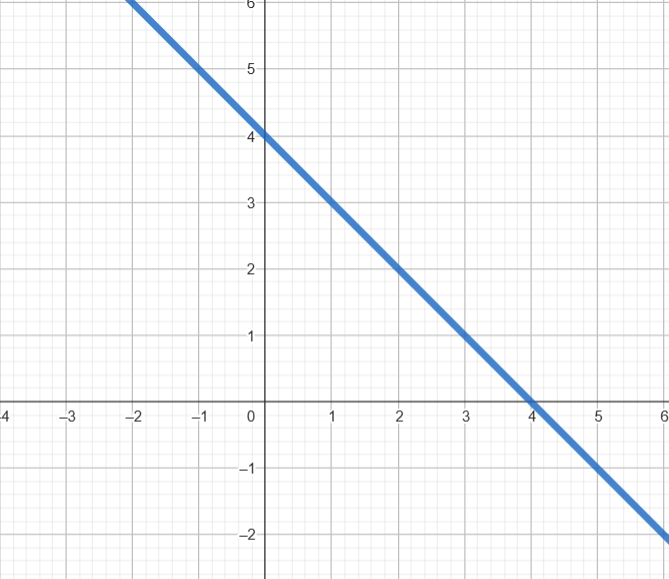
Função c) \( y = \dfrac{1}{2} – x \)
- Reescrevendo: \( y = -x + \dfrac{1}{2} \)
- Coeficiente angular: \( a = -1 \), intercepto: \( b = 0{,}5 \)
- Ponto 1: \( x = 0 \Rightarrow y = 0{,}5 \) → \( (0, 0{,}5) \)
- Ponto 2: \( x = 1 \Rightarrow y = -0{,}5 \) → \( (1, -0{,}5) \)
✅ Trace a reta passando por (0, 0,5) e (1, -0,5)
c)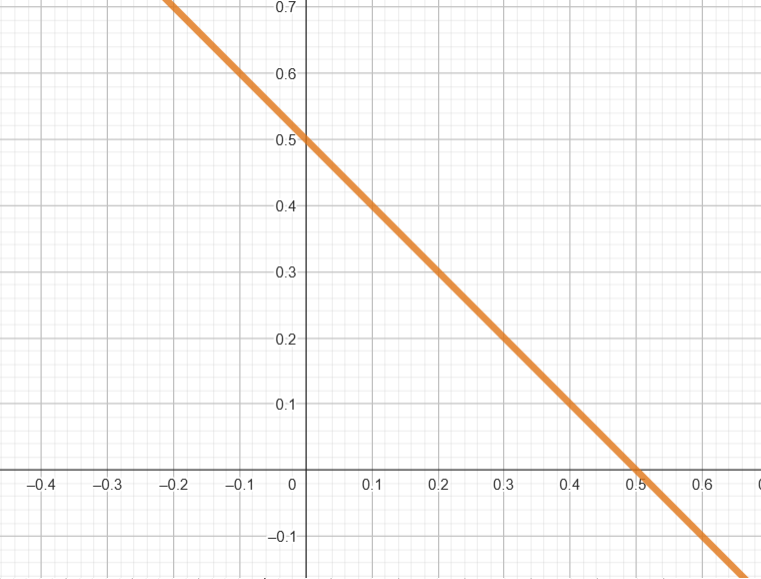
Função d) \( h(x) = -2x \)
- Coeficiente angular: \( a = -2 \), intercepto: \( b = 0 \) (passa pela origem)
- Ponto 1: \( x = 0 \Rightarrow h(0) = 0 \) → \( (0, 0) \)
- Ponto 2: \( x = 1 \Rightarrow h(1) = -2 \) → \( (1, -2) \)
✅ Trace a reta passando por (0, 0) e (1, -2)
d)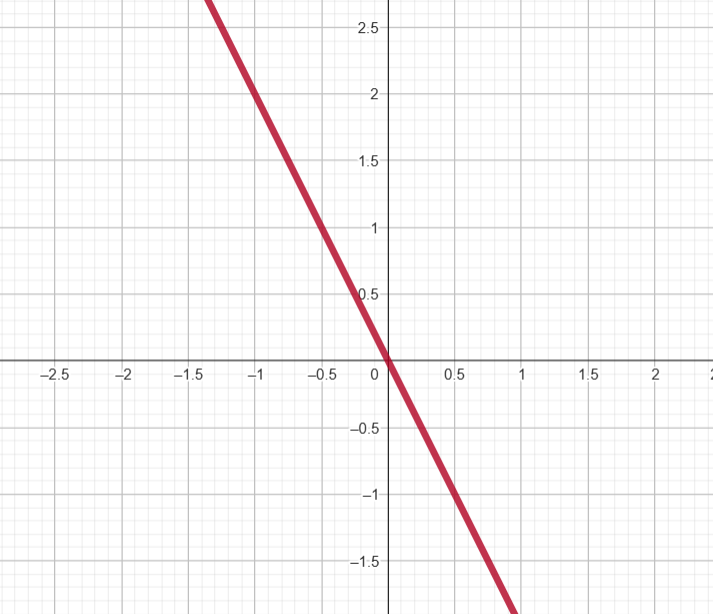
🧠 Dica: Use dois pontos por função e conecte-os com régua para construir os gráficos corretamente no plano cartesiano.






















