Inequação do Segundo Grau
Entenda passo a passo como resolver inequações quadráticas com teoria, gráficos e exercícios práticos.
O que é Inequação do Segundo Grau?
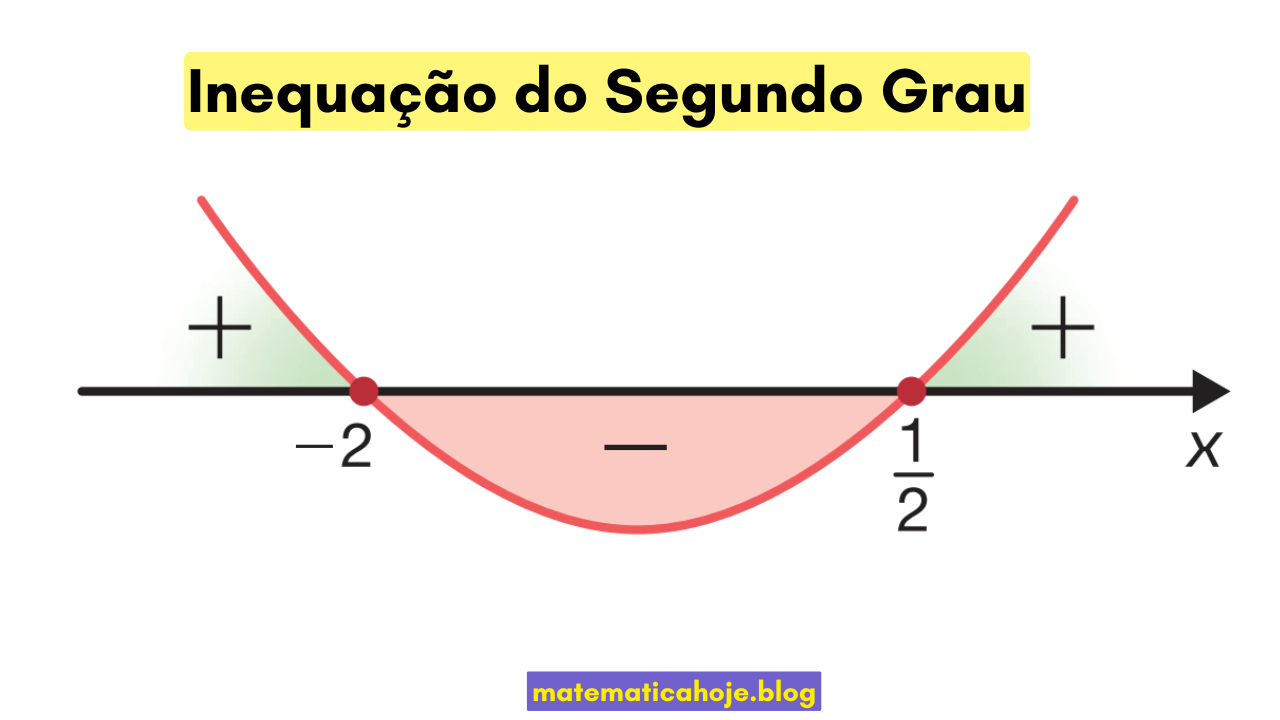
A inequação do segundo grau é uma desigualdade matemática que envolve uma função quadrática. Assim como nas funções quadráticas, sua representação gráfica é uma parábola. A resolução depende do estudo da variação de sinais dessa parábola.
ax² + bx + c > 0 ou ax² + bx + c < 0, com a ≠ 0.
Passo a passo da resolução
Para resolver inequações quadráticas, siga o roteiro:
- Identifique os coeficientes a, b e c.
- Calcule o discriminante (Δ): Δ = b² – 4ac.
- Encontre as raízes da equação associada ax² + bx + c = 0.
- Analise o sinal da parábola com base na concavidade (se a > 0, concavidade para cima; se a < 0, concavidade para baixo).
- Determine os intervalos da solução usando a imagem da função e o vértice.
Baixe grátis o eBook Fórmulas Matemática
Exercícios Resolvidos
Exercício 1: Resolva a inequação x² + x – 2 > 0.
Equação associada: x² + x – 2 = 0
Δ = 1² – 4·1·(-2) = 1 + 8 = 9
Raízes: x = (-1 ± 3)/2 → x₁ = -2, x₂ = 1
Concavidade: para cima (a = 1 > 0)
Solução: x < -2 ou x > 1
Exercício 2: Resolva a inequação -x² + 3x + 4 ≥ 0.
Equação associada: -x² + 3x + 4 = 0
Δ = 3² – 4·(-1)·4 = 9 + 16 = 25
Raízes: x = (-3 ± 5)/(-2) → x₁ = -1, x₂ = 4
Concavidade: para baixo (a = -1)
Solução: -1 ≤ x ≤ 4
Exercício 3: (Múltipla escolha) A solução da inequação x² – 5x + 6 < 0 é:
- a) x < 2 ou x > 3
- b) 2 < x < 3
- c) x ≤ 2 ou x ≥ 3
- d) Nenhuma das anteriores
Δ = (-5)² – 4·1·6 = 25 – 24 = 1
Raízes: x = (5 ± 1)/2 → x₁ = 2, x₂ = 3
Concavidade para cima (a = 1)
Gráfico negativo entre as raízes.
Solução: 2 < x < 3 → Alternativa (b)
Conclusão
A resolução de inequações do segundo grau está diretamente ligada ao estudo da parábola e de suas propriedades. Para aprofundar seus estudos, veja também:
- Variação de sinal da função quadrática
- Imagem da função quadrática
- Concavidade da parábola
- Vértice da parábola













