Uma inequação exponencial é toda desigualdade que apresenta a incógnita no expoente de, pelo menos, uma potência de base real positiva e diferente de 1. Essas inequações aparecem em contextos que envolvem crescimento ou decrescimento acelerado, como juros compostos ou processos biológicos.
O que é uma inequação exponencial?
Quando a incógnita está no expoente, e a base é positiva e diferente de 1, temos uma inequação exponencial. Veja alguns exemplos:
- \( 5^x < 1 \)
- \( \left(\frac{1}{2}\right)^{2x+1} > 4^x \)
- \( 10^x \geq -0{,}1 \)
- \( 22^{x+1} \cdot 4^{x-1} \leq \frac{1}{32} \)
Propriedades importantes
Para resolver inequações exponenciais, consideramos o comportamento da função \( f(x) = a^x \):
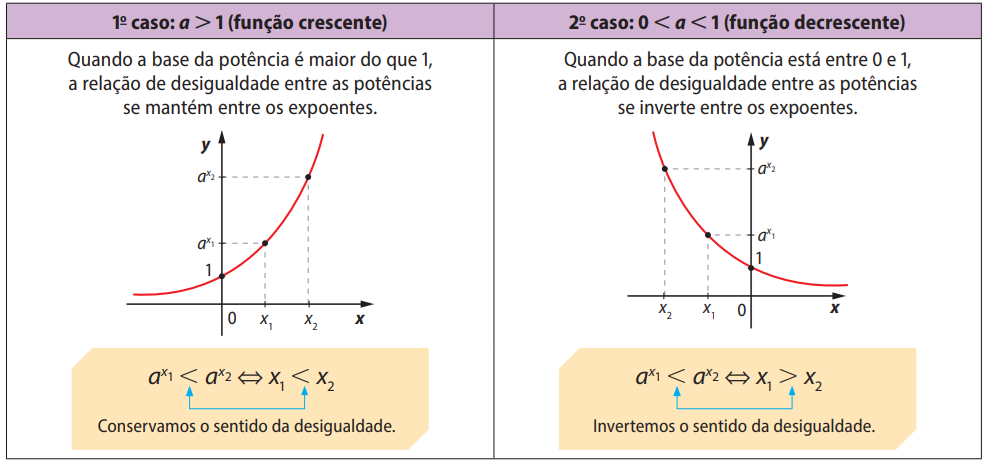
1º caso: \( a > 1 \) (função crescente)
Quando a base da potência é maior do que 1, a desigualdade entre as potências se mantém entre os expoentes:
\( a^{x_1} < a^{x_2} \Leftrightarrow x_1 < x_2 \)
2º caso: \( 0 < a < 1 \) (função decrescente)
Quando a base está entre 0 e 1, a desigualdade se inverte ao comparar os expoentes:
\( a^{x_1} < a^{x_2} \Leftrightarrow x_1 > x_2 \)
Exemplos Resolvidos Passo a Passo
Exemplo 1: \( 5^x < 1 \)
Passo 1:
Escreva 1 como potência de 5: \( 1 = 5^0 \)
\( 5^x < 5^0 \Rightarrow x < 0 \)
Resposta: \( S = (-\infty,\ 0) \)
Exemplo 2: \( \left(\frac{1}{2}\right)^{2x+1} > 4^x \)
Passo 1:
Reescreva as potências com base 2:
\( \left(\frac{1}{2}\right)^{2x+1} = 2^{-(2x+1)} \), e \( 4^x = (2^2)^x = 2^{2x} \)
\( 2^{-(2x+1)} > 2^{2x} \Rightarrow -(2x+1) > 2x \Rightarrow -1 > 4x \Rightarrow x < -\frac{1}{4} \)
Resposta: \( S = (-\infty,\ -\tfrac{1}{4}) \)
Exemplo 3: \( 10^x \geq -0{,}1 \)
Observação: A função \( 10^x \) é sempre positiva. Como \( -0{,}1 \) é negativo, a inequação é sempre verdadeira.
Resposta: \( S = \mathbb{R} \)
Exemplo 4: \( 22^{x+1} \cdot 4^{x-1} \leq \frac{1}{32} \)
Passo 1:
Reescreva com base 2:
\( 4 = 2^2 \Rightarrow 4^{x-1} = 2^{2x – 2} \), e \( \frac{1}{32} = 2^{-5} \)
\( 22^{x+1} \cdot 2^{2x – 2} \leq 2^{-5} \)
Observação: Como temos bases diferentes (22 e 2), não é possível comparar diretamente os expoentes. Este caso pode ser resolvido por logaritmos ou métodos numéricos.
Conclusão
As inequações exponenciais são resolvidas observando o comportamento da função exponencial. O segredo está em transformar os dois lados da inequação em potências com a mesma base e analisar:
- Se \( a > 1 \): mantém-se o sentido da desigualdade.
- Se \( 0 < a < 1 \): inverte-se o sentido da desigualdade.
Dominar essas propriedades facilita a resolução de diversos problemas envolvendo desigualdades exponenciais no cotidiano e em provas.