Integrais Definidas: Conceito, Aplicações e Exercícios Resolvidos

Integrais definidas - Interpretação geométrica

A integral definida é uma ferramenta fundamental do cálculo que permite calcular áreas, volumes, deslocamentos, trabalho e diversas outras grandezas físicas e geométricas. Diferente da integral indefinida, que representa uma família de funções, a integral definida está associada a um valor numérico.

O que é uma Integral Definida?

Dada uma função contínua \( f(x) \) em um intervalo \([a,b]\), a integral definida é representada por:

\[ \int_a^b f(x)\,dx \]

Esse símbolo representa a área líquida entre o gráfico de \( f(x) \) e o eixo x, no intervalo de \( a \) até \( b \). O resultado pode ser positivo, negativo ou zero, dependendo da posição do gráfico em relação ao eixo.

Elementos da Integral Definida

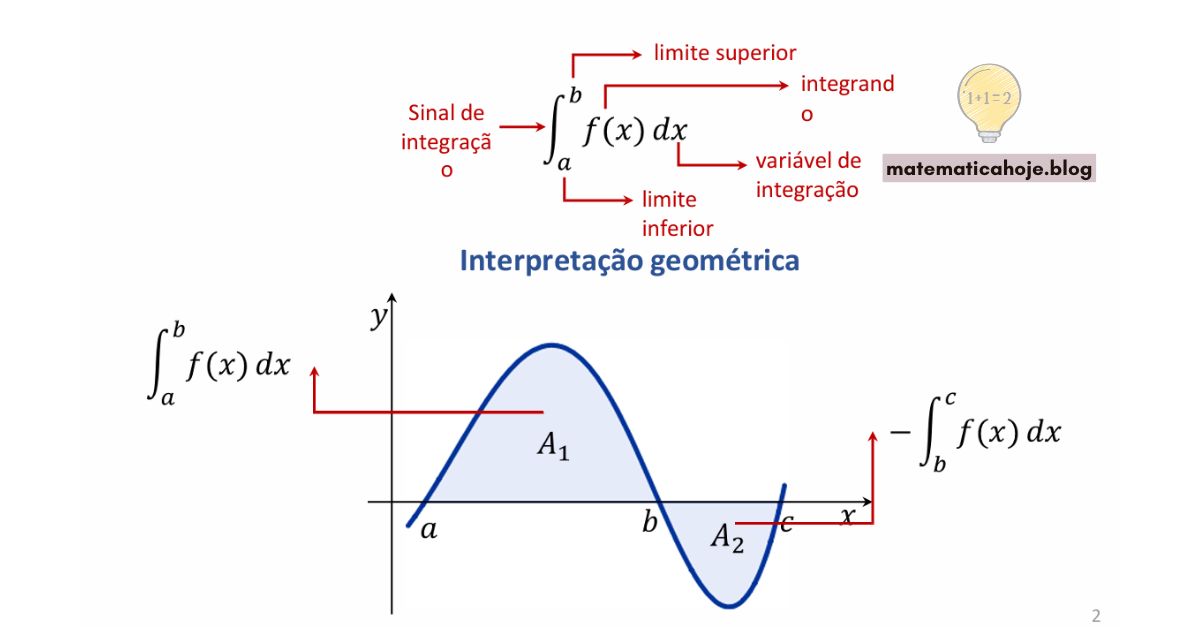
∫ → Sinal de integração
a → Limite inferior
b → Limite superior
f(x) → Integrando
dx → Variável de integração

Interpretação Geométrica

A integral definida pode ser interpretada geometricamente como a soma algébrica das áreas sob o gráfico de \( f(x) \). Quando \( f(x) > 0 \), a área é positiva; quando \( f(x) < 0 \), a área é negativa.

\[ \int_a^b f(x)\,dx = A_1 – A_2 \]

onde \( A_1 \) representa a área acima do eixo x e \( A_2 \) a área abaixo.

Teorema Fundamental do Cálculo

Esse teorema conecta derivadas e integrais, mostrando que a integração é o processo inverso da diferenciação.

\[ \int_a^b f(x)\,dx = F(b) – F(a) \]

Ou seja, para calcular uma integral definida, basta encontrar uma antiderivada \( F(x) \) de \( f(x) \) e aplicar os limites.

Aplicações das Integrais Definidas

As integrais definidas aparecem em várias áreas do conhecimento:

Física: cálculo de trabalho, energia, torque e centro de massa.
Engenharia: volume de reservatórios e áreas sob curvas de esforço.
Economia: cálculo de custo e lucro total.
Probabilidade e Estatística: determinação da área sob uma curva de densidade.

💡 Dica: A integral definida é o caminho natural após estudar a integral indefinida, pois fornece significado prático aos resultados obtidos.

Exemplos Resolvidos Passo a Passo

Exemplo 1 – Área sob uma parábola

Calcule \( \displaystyle \int_0^2 (x^2+1)\,dx \).

👀 Ver solução passo a passo

\[ \int_0^2 (x^2+1)\,dx = \left[\frac{x^3}{3} + x\right]_0^2 \] \[ = \left(\frac{8}{3}+2\right) – (0) \] \[ = \frac{14}{3} \]

Resultado: \( \frac{14}{3} \)

Exemplo 2 – Área negativa

Calcule \( \displaystyle \int_{0}^{\pi} \sin x\,dx \).

👀 Ver solução passo a passo

\[ \int_0^{\pi} \sin x\,dx = [-\cos x]_0^{\pi} \] \[ = [-\cos(\pi)] – [-\cos(0)] \] \[ = [1 – (-1)] = 2 \]

Resultado: 2 (área positiva acima do eixo x).

Exemplo 3 – Integral com limites trocados

Mostre que \( \displaystyle \int_b^a f(x)\,dx = -\int_a^b f(x)\,dx \).

👀 Ver explicação

Ao inverter os limites de integração, o sinal da área também se inverte. Logo, trocar \( a \) por \( b \) muda o sinal do resultado: \[ \int_b^a f(x)\,dx = -\int_a^b f(x)\,dx \]

📘 Domine os fundamentos do cálculo: 👉 Baixe o eBook Fórmulas Matemáticas

Lista de Exercícios

\( \displaystyle \int_1^3 x^2\,dx \)
\( \displaystyle \int_0^2 (2x+1)\,dx \)
\( \displaystyle \int_0^{\pi/2} \cos x\,dx \)
\( \displaystyle \int_0^1 (x^3 – 4x)\,dx \)
\( \displaystyle \int_1^e \frac{1}{x}\,dx \)

📘 Mostrar gabarito

\( \frac{26}{3} \)
\( 4 \)
\( 1 \)
\( -\frac{7}{4} \)
\( 1 \)

Conclusão

A integral definida é uma das ferramentas mais poderosas da matemática aplicada. Além de permitir o cálculo de áreas e volumes, ela conecta conceitos de variação (derivada) e acumulação (integração), sendo indispensável em física, engenharia e economia.

🎯 Continue aprendendo:
👉 Regra da Substituição nas Integrais
👉 Integrais Indefinidas e Antiderivadas
👉 Mapas Mentais de Matemática