Explore uma seleção completa com 10 questões resolvidas e comentadas sobre intervalos reais, notação de conjuntos, operações com união, interseção e diferença, além de representações na reta real. Ideal para alunos do ensino médio, candidatos à OBMEP, vestibulares como Fuvest e também para concursos públicos que exigem domínio da Teoria dos Conjuntos.
Cada item vem com interpretação gráfica ou algébrica, fórmulas e raciocínio passo a passo.
Questão 1 – Conjuntos Numéricos e Intervalos Reais
Enunciado:
Determine os elementos dos conjuntos:
a) \( A = \{x \in \mathbb{N} \mid 3x – 4x – 4 = 0\} \)
b) \( B = \{y \in \mathbb{R} \mid y^2 – 7 = 0\} \)
c) \( C = \left\{a \in \mathbb{N} \mid \frac{a}{4} + 0{,}25a + \frac{3}{2}a = 2\right\} \)
d) \( D = \{x \in \mathbb{Q} \mid 3 + x^2 = 4\} \)
e) \( E = \left\{y \in \mathbb{Q} \mid \frac{y}{3} + y = \frac{1}{7} \right\} \)
f) \( F = \{x \in \mathbb{R} \mid x^2 – 4 = 0\} \)
Ver Solução
a) Resolvendo \( 3x – 4x – 4 = 0 \Rightarrow -x – 4 = 0 \Rightarrow x = -4 \)
Como \( x \in \mathbb{N} \) e -4 não é natural: \( A = \emptyset \)
b) \( y^2 – 7 = 0 \Rightarrow y = \pm\sqrt{7} \)
Como \( y \in \mathbb{R} \): \( B = \{-\sqrt{7}, \sqrt{7}\} \)
c) \( \frac{a}{4} + 0{,}25a + \frac{3}{2}a = 2 \)
Convertendo tudo para frações: \( \frac{a}{4} + \frac{a}{4} + \frac{3a}{2} = 2 \Rightarrow \frac{2a}{4} + \frac{3a}{2} = 2 \)
Somando: \( \frac{a}{2} + \frac{3a}{2} = 2 \Rightarrow \frac{4a}{2} = 2 \Rightarrow 2a = 2 \Rightarrow a = 1 \)
\( C = \{1\} \)
d) \( 3 + x^2 = 4 \Rightarrow x^2 = 1 \Rightarrow x = \pm1 \)
Como \( x \in \mathbb{Q} \): \( D = \{-1, 1\} \)
e) \( \frac{y}{3} + y = \frac{1}{7} \Rightarrow \frac{4y}{3} = \frac{1}{7} \Rightarrow y = \frac{3}{28} \)
\( E = \left\{ \frac{3}{28} \right\} \)
f) \( x^2 – 4 = 0 \Rightarrow x = \pm2 \)
\( F = \{-2, 2\} \)
Resumo: Esta questão explora a solução de equações sob restrição de conjuntos: Naturais, Racionais e Reais. Importante observar o conjunto ao qual a solução precisa pertencer.
🧠 Mapas Mentais de Matemática
Questão 2 – Expressões com Raízes Irracionais
Enunciado:
Sendo \( \sqrt{3} \approx 1{,}732 \), calcule um valor aproximado de:
a) \( \frac{\sqrt{3} + 2}{2} \)
b) \( \frac{2\sqrt{3} – 1}{4} \)
Ver Solução
a) Usando \( \sqrt{3} \approx 1{,}732 \):
\[ \frac{\sqrt{3} + 2}{2} \approx \frac{1{,}732 + 2}{2} = \frac{3{,}732}{2} = 1{,}866 \]
Resultado aproximado: 1,866
b) Usando \( \sqrt{3} \approx 1{,}732 \):
\[ \frac{2\sqrt{3} – 1}{4} \approx \frac{2 \cdot 1{,}732 – 1}{4} = \frac{3{,}464 – 1}{4} = \frac{2{,}464}{4} = 0{,}616 \]
Resultado aproximado: 0,616
Resumo: Esta questão mostra como utilizar aproximações numéricas de radicais para facilitar o cálculo de expressões. Aqui, usamos \( \sqrt{3} \approx 1{,}732 \) e aplicamos operações básicas de adição, subtração e divisão para encontrar os valores pedidos.
🧠 Mapas Mentais de Matemática
Questão 3 – Propriedades de Números Irracionais
Enunciado:
Sejam \( a \) e \( b \) números irracionais quaisquer. As seguintes afirmações são FALSAS:
a) \( a \cdot b \) sempre é um número irracional;
b) \( a + b \) sempre é um número irracional.
Em cada caso, dê um exemplo que indica que as afirmações são falsas.
Ver Solução
a) Vamos dar um exemplo onde \( a \cdot b \) não é irracional.
Seja \( a = \sqrt{2} \) e \( b = \sqrt{2} \). Ambos são irracionais.
Multiplicando: \( a \cdot b = \sqrt{2} \cdot \sqrt{2} = 2 \), que é racional.
Contraexemplo: \( a = \sqrt{2},\ b = \sqrt{2} \Rightarrow a \cdot b = 2 \in \mathbb{Q} \)
b) Vamos dar um exemplo onde \( a + b \) não é irracional.
Seja \( a = \sqrt{2} \) e \( b = -\sqrt{2} \). Ambos são irracionais.
Somando: \( a + b = \sqrt{2} + (-\sqrt{2}) = 0 \), que é racional.
Contraexemplo: \( a = \sqrt{2},\ b = -\sqrt{2} \Rightarrow a + b = 0 \in \mathbb{Q} \)
Resumo: Nem todo produto ou soma de irracionais resulta em outro irracional. Contraexemplos como esses são fundamentais para entender que algumas propriedades não são válidas para todos os casos.
🧠 Mapas Mentais de Matemática
Questão 4– Números Reais: Análise de Racionalidade
Enunciado:
Assinale a afirmação verdadeira:
- a) \( (\sqrt{3} + 1)(\sqrt{3} – 1) \) é irracional e \( 0{,}999\ldots \) é racional.
- b) \( (\sqrt{3} + 1)(\sqrt{3} – 1) \) é racional e \( 0{,}999\ldots \) é racional.
- c) \( (\sqrt{3} + 1)(\sqrt{3} – 1) \) é racional e \( 0{,}999\ldots \) é irracional.
- d) \( (\sqrt{3} + 1)(\sqrt{3} – 1) \) é irracional e \( 0{,}999\ldots \) é irracional.
- e) \( (\sqrt{3} + 1)(\sqrt{3} – 1) \) e \( 0{,}999\ldots \) não são números reais.
Ver Solução
Análise de: \( (\sqrt{3} + 1)(\sqrt{3} – 1) \)
Esse é um produto notável da forma \( (a + b)(a – b) = a^2 – b^2 \).
\[ (\sqrt{3} + 1)(\sqrt{3} – 1) = (\sqrt{3})^2 – (1)^2 = 3 – 1 = 2 \]
Logo, o resultado é racional.
Análise de: \( 0{,}999\ldots \)
Esse valor é uma dízima periódica e é matematicamente equivalente a 1.
\[ 0{,}999\ldots = 1 \quad \Rightarrow \quad \text{É um número racional.} \]
Portanto, a única alternativa totalmente correta é:
Letra b) – Ambas as expressões são racionais.
🧠 Mapas Mentais de Matemática
Questão 5 – Intervalos e Notação de Conjuntos
Enunciado:
Usando a notação de conjuntos, escreva os intervalos a seguir:
- a) \([6, 10]\)
- b) \( ]-1,\ 5] \)
- c) \(-6,\ 0[ \)
- d) \([0,\ +\infty[ \)
- e) \( ]-\infty,\ 3[ \)
Ver Solução
a) \([6,\ 10]\) representa todos os reais entre 6 e 10, inclusive.
\( \{x \in \mathbb{R} \mid 6 \leq x \leq 10\} \)
b) \( ]-1,\ 5] \) representa todos os reais maiores que -1 e menores ou iguais a 5.
\( \{x \in \mathbb{R} \mid -1 < x \leq 5\} \)
c) \( ]-6,\ 0[ \) representa todos os reais estritamente entre -6 e 0.
\( \{x \in \mathbb{R} \mid -6 < x < 0\} \)
d) \([0,\ +\infty[ \) representa todos os reais a partir de 0 (inclusive).
\( \{x \in \mathbb{R} \mid x \geq 0\} \)
e) \( ]-\infty,\ 3[ \) representa todos os reais menores que 3.
\( \{x \in \mathbb{R} \mid x < 3\} \)
Resumo: A conversão de intervalos para notação de conjuntos é essencial para compreender a estrutura da reta real. Atenção ao uso de colchetes e parênteses, pois eles indicam se os extremos estão incluídos ou não.
🧠 Mapas Mentais de Matemática
Questão 6 – Intervalos Representados na Reta Real
Enunciado:
Represente, na reta real, os intervalos a seguir:
- a) \([2, 8]\)
- b) \( ]-\infty, 2] \)
- c) \([-6, -1[ \)
- d) \([2, +\infty[ \)
- e) \( \{x \in \mathbb{R} \mid 2 < x < 5\} \)
- f) \( \{x \in \mathbb{R} \mid -2 \leq x \leq 2\} \)
Ver Solução
a) Intervalo fechado em ambos os extremos: inclui os valores 2 e 8.
Representação: \([2, 8]\)
b) Intervalo aberto à esquerda e fechado em 2: todos os reais menores ou iguais a 2.
Representação: \( ]-\infty, 2] \)
c) Intervalo fechado em -6 e aberto em -1.
Representação: \([-6, -1[ \)
d) Intervalo fechado em 2 e sem limite superior (vai até \(+\infty\)).
Representação: \([2, +\infty[ \)
e) Intervalo com desigualdades estritas (sem incluir os extremos).
Representação: \( ]2, 5[ \)
f) Intervalo fechado de -2 a 2 (ambos incluídos).
Representação: \([-2, 2]\)
Resumo: Saber converter entre desigualdades, notação de conjuntos e intervalos é essencial para a compreensão da reta real e dos subconjuntos dos números reais. Os colchetes [ ] indicam inclusão e os parênteses ] [ indicam exclusão.
🧠 Mapas Mentais de Matemática
Questão 7 – Interpretação de Intervalos na Reta Real
Enunciado:
Usando a notação de conjuntos, escreva os intervalos a seguir, que estão representados na reta real:
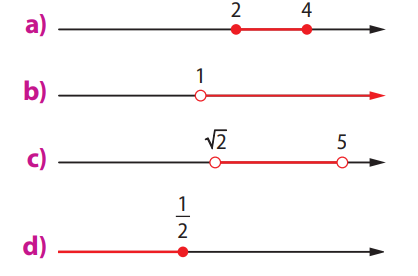
Ver Solução
a) Os pontos 2 e 4 estão preenchidos (fechados), indicando que eles pertencem ao intervalo.
\( \{x \in \mathbb{R} \mid 2 \leq x \leq 4\} \)
b) A partir de 1, com círculo aberto, indo para a direita: intervalo aberto em 1 e sem limite superior.
\( \{x \in \mathbb{R} \mid x > 1\} \)
c) Intervalo aberto de \( \sqrt{2} \) até 5 (ambos com círculos abertos).
\( \{x \in \mathbb{R} \mid \sqrt{2} < x < 5\} \)
d) Reta indo para a esquerda até \( \frac{1}{2} \), com ponto fechado.
\( \{x \in \mathbb{R} \mid x \leq \frac{1}{2} \} \)
Resumo: A leitura correta de gráficos na reta real exige atenção ao tipo de ponto (aberto ou fechado) e à direção do traçado. A notação de conjuntos permite representar com precisão esses intervalos.
🧠 Mapas Mentais de Matemática
Questão 8 – União de Conjuntos Numéricos
Enunciado:
Determine \( A \cup B \) em cada caso:
- \( A = \{x \in \mathbb{R} \mid 0 < x < 3\} \) e \( B = \{x \in \mathbb{R} \mid 1 < x < 5\} \)
- \( A = \{x \in \mathbb{R} \mid -4 < x \leq 1\} \) e \( B = \{x \in \mathbb{R} \mid 2 \leq x \leq 3\} \)
- \( A = \{x \in \mathbb{R} \mid 2 < x < 5\} \) e \( B = \{x \in \mathbb{R} \mid 1 < x < 4\} \)
- \( A = \{x \in \mathbb{R} \mid -2 \leq x < 2\} \) e \( B = \{x \in \mathbb{R} \mid x \geq 0\} \)
Ver Solução
a)
\[ A = (0, 3), \quad B = (1, 5) \]
\[ A \cup B = (0, 5) \]
\( \{x \in \mathbb{R} \mid 0 < x < 5\} \)
b)
\[ A = (-4, 1], \quad B = [2, 3] \]
\[ A \cup B = (-4, 1] \cup [2, 3] \]
\( \{x \in \mathbb{R} \mid -4 < x \leq 1 \text{ ou } 2 \leq x \leq 3\} \)
c)
\[ A = (2, 5), \quad B = (1, 4) \]
\[ A \cup B = (1, 5) \]
\( \{x \in \mathbb{R} \mid 1 < x < 5\} \)
d)
\[ A = [-2, 2), \quad B = [0, +\infty[ \]
\[ A \cup B = [-2, +\infty[ \]
\( \{x \in \mathbb{R} \mid x \geq -2\} \)
Resumo: A união de conjuntos corresponde à junção de todos os elementos que pertencem a pelo menos um dos conjuntos. Ao trabalhar com intervalos, devemos observar os extremos e seus símbolos de inclusão (colchetes) ou exclusão (parênteses).
🧠 Mapas Mentais de Matemática
Questão 9 – Operações com Intervalos Reais
Enunciado:
Dados os conjuntos:
- \( A = [-1,\ 6[ \)
- \( B = ]-4,\ 2] \)
- \( E = ]-2,\ 4[ \)
Calcule:
- a)\( (B \cup E) – A \)
- b)\( E – (A \cap B) \)
Ver Solução
a) \( (B \cup E) – A \)
\[ B = (-4,\ 2], \quad E = (-2,\ 4) \]
\[ B \cup E = (-4,\ 4) \]
\[ A = [-1,\ 6[ \]
Agora fazemos: \( (-4,\ 4) – [-1,\ 6[ = (-4,\ -1[ \)
Resultado: \( (-4,\ -1[ \)
b) \( E – (A \cap B) \)
\[ A = [-1,\ 6[, \quad B = (-4,\ 2] \]
\[ A \cap B = [-1,\ 2] \]
\[ E = (-2,\ 4), \quad E – (A \cap B) = (-2,\ -1) \cup (2,\ 4) \]
Resultado: \( (-2,\ -1) \cup (2,\ 4) \)
Resumo: Para resolver operações entre conjuntos com intervalos, é fundamental observar os limites dos intervalos e se os extremos estão incluídos ou não. A diferença \( A – B \) significa remover do conjunto \( A \) os elementos que também estão em \( B \), enquanto união e interseção seguem as propriedades clássicas da Teoria dos Conjuntos.
🧠 Mapas Mentais de Matemática
Questão 10 – Fuvest-SP – Números Reais na Reta
Enunciado:
(Fuvest-SP) Na figura abaixo estão representados geometricamente os números reais \(0\), \(x\), \(y\) e \(1\). A posição do número real \(x \cdot y\) é:

- à esquerda do zero
- entre zero e x
- entre x e y
- entre y e 1
- à direita de 1
Ver Solução
Sabemos que \( 0 < x < y < 1 \).
Multiplicando dois números reais positivos menores que 1, o produto será menor que ambos:
\[ 0 < x < y < 1 \quad \Rightarrow \quad 0 < x \cdot y < x \]
Portanto, \( x \cdot y \) está entre 0 e x.
Alternativa correta: b) entre zero e x
Resumo: Quando multiplicamos dois números reais entre 0 e 1, o produto sempre fica mais próximo de zero do que qualquer um dos fatores. Esse tipo de interpretação é essencial em provas como Fuvest, OBMEP e vestibulares em geral.
🧠 Mapas Mentais de Matemática

























