ITA 2024 — 1ª Fase — Questão 45 — Geometria Plana
Considere um triângulo \(ABC\) e \(M\) o ponto médio do lado \(BC\).
Tome o ponto \(R \neq A\) na reta \(AB\) tal que \(m(AB) = m(BR)\) e o ponto \(Q\) na reta \(AC\) tal que \(m(AC) = 2m(CQ)\) e \(Q\) não esteja no segmento \(AC\).
A reta \(RM\) corta o lado \(AC\) no ponto \(S\) e a reta \(QM\) corta o lado \(AB\) no ponto \(P\).
Sendo \(24\) a área do triângulo \(ABC\), o valor da área do quadrilátero \(APMS\) é:
Alternativas:
a) 15 b) 16 c) 17 d) 18 e) 19
👀 Solução Passo a Passo
1) Construção da figura:
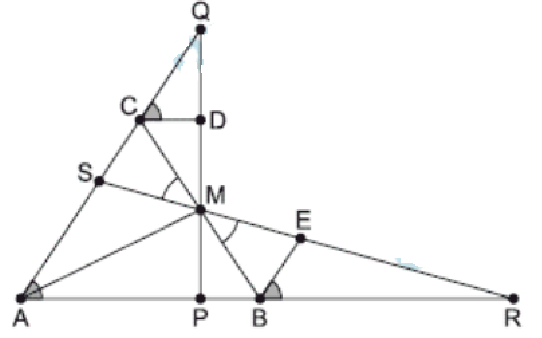 A partir das informações, identificamos os pontos \(M, R, Q, S, P\) e segmentos auxiliares paralelos a \(AB\) e \(AC\).
A partir das informações, identificamos os pontos \(M, R, Q, S, P\) e segmentos auxiliares paralelos a \(AB\) e \(AC\).
2) Semelhança de triângulos:
Pelos triângulos \(\triangle QCD \sim \triangle QAP\), temos: \[ \frac{CD}{AP} = \frac{QD}{QP} = \frac{QC}{QA} = \frac{QC}{QC + AC} = \frac{QC}{3QC} = \frac13 \] Logo, \(AP = 3CD\) e \(QP = 3QD\).
3) Congruência de triângulos:
\(\triangle CDM \cong \triangle BPM\) implica \(CD = BP\). Assim: \[ AP = 3BP \]
Pela semelhança \(\triangle BER \sim \triangle ASR\), deduzimos: \[ AS = 2BE \quad \text{e} \quad SR = 2ER \]
4) Outras congruências:
\(\triangle CSM \cong \triangle BEM\) implica \(CS = BE\), logo: \[ AS = 2CS \]
5) Área de \(\triangle ABM\):
Mesmo base e altura que \(\triangle ABC\), resultando: \[ A_{ABM} = \frac12 \cdot A_{ABC} = 12 \]
6) Área de \(\triangle APM\):
Com \(AB = 3BP + BP = 4BP\): \[ A_{ABM} = 4 \cdot A_{APM} \quad \Rightarrow \quad A_{APM} = 3 \]
7) Área de \(\triangle ASM\):
Mesmo altura que \(AC\): \[ A_{ACM} = 3 \cdot A_{CSM} \quad \Rightarrow \quad A_{CSM} = 4 \]
8) Área final do quadrilátero \(APMS\):
\[ A_{APMS} = A_{ABC} – A_{APM} – A_{ASM} = 24 – 3 – 4 = 17 \]

2) Semelhança de triângulos:
Pelos triângulos \(\triangle QCD \sim \triangle QAP\), temos: \[ \frac{CD}{AP} = \frac{QD}{QP} = \frac{QC}{QA} = \frac{QC}{QC + AC} = \frac{QC}{3QC} = \frac13 \] Logo, \(AP = 3CD\) e \(QP = 3QD\).
3) Congruência de triângulos:
\(\triangle CDM \cong \triangle BPM\) implica \(CD = BP\). Assim: \[ AP = 3BP \]
Pela semelhança \(\triangle BER \sim \triangle ASR\), deduzimos: \[ AS = 2BE \quad \text{e} \quad SR = 2ER \]
4) Outras congruências:
\(\triangle CSM \cong \triangle BEM\) implica \(CS = BE\), logo: \[ AS = 2CS \]
5) Área de \(\triangle ABM\):
Mesmo base e altura que \(\triangle ABC\), resultando: \[ A_{ABM} = \frac12 \cdot A_{ABC} = 12 \]
6) Área de \(\triangle APM\):
Com \(AB = 3BP + BP = 4BP\): \[ A_{ABM} = 4 \cdot A_{APM} \quad \Rightarrow \quad A_{APM} = 3 \]
7) Área de \(\triangle ASM\):
Mesmo altura que \(AC\): \[ A_{ACM} = 3 \cdot A_{CSM} \quad \Rightarrow \quad A_{CSM} = 4 \]
8) Área final do quadrilátero \(APMS\):
\[ A_{APMS} = A_{ABC} – A_{APM} – A_{ASM} = 24 – 3 – 4 = 17 \]
Resposta: c) 17






















