Seja \(H\) uma hipérbole no plano cartesiano cujos focos são comuns aos focos da elipse \(E:\ \dfrac{x^2}{4}+y^2=1\).
Seja \(P\) um ponto de interseção de \(E\) e \(H\) no primeiro quadrante e a origem do sistema cartesiano. Sabendo que \(OP\) forma um ângulo \(\theta\) com o eixo horizontal \(Ox\), com \(\tan(\theta)=\dfrac{\sqrt{3}}{6}\), a excentricidade de \(H\) é:
👀 Solução passo a passo
Em \(E:\ \dfrac{x^2}{4}+y^2=1\) temos \(a=2\), \(b=1\). Logo \(f^2=a^2-b^2=4-1=3\Rightarrow f=\sqrt{3}\). Assim, os focos são \((\pm \sqrt{3},0)\) e serão também os focos da hipérbole \(H\).
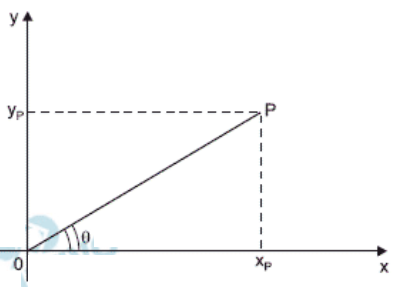
Como \(\tan\theta = \dfrac{y_P}{x_P}=\dfrac{\sqrt{3}}{6}\), temos \(y_P=\dfrac{\sqrt{3}}{6}x_P\). Substituindo em \(E\):
\[ \frac{x_P^2}{4} + \left(\frac{\sqrt{3}}{6}x_P\right)^2 = \frac{x_P^2}{4} + \frac{x_P^2}{12} = \frac{4x_P^2}{12} = \frac{x_P^2}{3} = 1 \ \Rightarrow\ x_P=\sqrt{3},\quad y_P=\frac{1}{2}. \]Com centro na origem e eixo transverso no eixo \(x\): \(\dfrac{x^2}{a’^2}-\dfrac{y^2}{b’^2}=1\). Para hipérbole: \(c^2=f^2=a’^2+b’^2=3\Rightarrow b’^2=3-a’^2\).
Substituindo em \(\dfrac{x^2}{a’^2}-\dfrac{y^2}{b’^2}=1\):
\[ \frac{3}{a’^2} – \frac{1/4}{b’^2} = 1,\quad b’^2=3-a’^2. \] \[ \frac{3}{a’^2} – \frac{1}{4(3-a’^2)} = 1 \ \Rightarrow\ 4a’^4 – 25a’^2 + 36 = 0. \]Resolvendo em \(A=a’^2\): \(4A^2-25A+36=0 \Rightarrow A\in\left\{4,\ \dfrac{9}{4}\right\}\). Como \(b’^2=3-A>0\), fica \(a’^2=\dfrac{9}{4}\Rightarrow a’=\dfrac{3}{2}\).






















